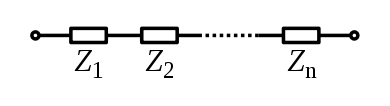עכבה חשמלית

מתוך ויקיפדיה, האנציקלופדיה החופשית

עכבה חשמלית, הנקראת גם אימפדנס, הוא מידת ההתנגדות הכוללת של מעגל חשמלי. מושג העכבה מהווה הכללה של חוק אוהם לניתוח מעגל זרם חילופין. לשני הגדלים משתמשים באותה היחידה, האוהם (Ω) ב-SI.

תוכן עניינים

1 מצב מתמיד סינוסי
2 הגדרה וסימון האימפדנס החשמלי
3 אימפדנס של רכיבים
4 היגב
5 חיבור אימפדנסים
- 5.1 בטור
- 5.2 במקביל
6 מעגלים עם מקורות כלליים
7 גודל ופאזה של אימפדנס
8 פאזור שיא מול פאזור שורש הממוצע הריבועי
9 ראו גם
10 קישורים חיצוניים
11 מקורות

[עריכה] מצב מתמיד סינוסי

באופן כללי, פתרונות המתחים והזרמים במעגל המכיל נגדים, קבלים וסלילים הם פתרונות למשוואה דיפרנציאלית רגילה. ניתן להראות שאם מקורות המתח והזרם במעגל הם סינוסיים ובעלי תדירות קבועה, הפתרונות מקבלים צורה הנקראת מצב מתמיד סינוסי (מצב מתמיד במעגל AC), כלומר כל המתחים והזרמים במעגל הם סינוסיים ובעלי אמפליטודה, תדירות ופאזה קבועות.

במצב מתמיד סינוסי, $v(t) \!\$ היא פונקציה סינוסית של הזמן עם אמפליטודה קבועה $V_\mathrm{p} \!\$ , תדירות קבועה $f \!\$ , ופאזה קבועה $\varphi \!\$ :

$v(t) = V_\mathrm{p} \cos \left( 2 \pi f t + \varphi \right) = \Re \left( V_\mathrm{p} e^{j 2 \pi f t} e^{j \varphi} \right)$

כאשר:

$j \!\$ היא היחידה המדומה $\sqrt{-1}$

$\Re (z)$ נותן את החלק הממשי של המספר המרוכב $z \!\$

הייצוג הפאזורי של $v(t) \!\$ הוא הקבוע המרוכב $V \!\$ :

$V = V_\mathrm{p} e^{j \varphi}$

במעגל במצב מתמיד סינוסי, לכל המתחים והזרמים במעגל יש ייצוגים פאזוריים בתנאי שכל המקורות המתח והזרם הם באותה התדירות, כך שכל מתח וזרם ניתן לייצוג כמספר מרוכב קבוע. בניתוח מעגל DC, כל מתח וזרם ניתן לייצוג כמספר ממשי. לכן, ניתן לשער שהחוקים שפותחו לניתוח מעגל DC ניתנים ליישום לניתוח מעגל AC על ידי שימוש במספרים מרוכבים במקום מספרים ממשיים.

[עריכה] הגדרה וסימון האימפדנס החשמלי

אימפדנסים כלליים במעגל ניתנים לסימון בעזרת סימון של נגד או בעזרת קופסה עם תווית.

האימפדנס של רכיב במעגל מוגדר כיחס בין פאזור המתח הנופל על הרכיב לפאזור הזרם העובר דרך הרכיב:

$Z_\mathrm{R} = \frac{V_\mathrm{r}}{I_\mathrm{r}}$

חשוב לציין כי למרות ש- $Z \!\$ הוא היחס בין שני פאזורים, $Z \!\$ עצמו אינו פאזור, כלומר $Z \!\$ אינו קשור לפונקציה סינוסית כלשהי של הזמן.

במעגלי DC, ההתנגדות מוגדרת על פי חוק אוהם להיות היחס בין מתח ה-DC הנופל על הנגד לזרם ה-DC דרך הנגד:

$R = \frac{V_\mathrm{R}}{I_\mathrm{R}}$

כאשר:

$V_\mathrm{R} \!\$ ו- $I_\mathrm{R} \!\$ הם ערכי ה-DC (ממשיים)

כלומר הגדרת האימפדנס מהווה הכללה של חוק אוהם, כאשר את התנגדות הנגד $R \!\$ במעגל ה-DC מחליפים באימפדנס שלו $Z_\mathrm{R} \!\$ במעגל ה-AC. הכללה זו של חוק אוהם אינה מוגבלת לנגדים, וניתן להשתמש בה גם לקבלים ולסלילים במעגל AC.

כפי שמכלילים את חוק אוהם למעגלי AC בעזרת השימוש בפאזורים, מכלילים גם תוצאות נוספות ממעגלי DC למעגלי AC כמו חלוקת מתח, חלוקת זרם, משפט תבנין ומשפט נורטון.

הגודל ההופכי של התנגדות טהורה נקרא מוליכות. על ידי הכללה דומה למעגלי AC מגדירים שהגודל ההופכי של אימפדנס נקרא אדמיטנס הנמדד ביחידות SI בסימנס:

$Y = Z^{-1} = 1/Z \,$

[עריכה] אימפדנס של רכיבים

עבור נגד:

$Z_\mathrm{resistor} = \frac{V_\mathrm{R}}{I_\mathrm{R}} = R \,$

עבור קבל:

$Z_\mathrm{capacitor} = \frac{V_\mathrm{C}}{I_\mathrm{C}} = \frac{1}{j \omega C} \ = \frac{-j}{\omega C} \,$

עבור סליל:

$Z_\mathrm{inductor} = \frac{V_\mathrm{L}}{I_\mathrm{L}} = j \omega L \,$

[עריכה] היגב

המונח היגב, (ריאקטנס) או התנגדות ראקטיבית מתייחס לחלק המדומה של האימפדנס. להלן מספר דוגמאות:

האימפדנס של נגד הוא $R \!\$ (ההתנגדות שלו) והריאקטנס שלו הוא $0 \!\$ .
האימפדנס של קבל הוא $j(-1/\omega C) \!\$ והריאקטנס שלו הוא - $-1/\omega C \!\$ .
האימפדנס של סליל הוא $j\omega L \!\$ והריאקטנס שלו הוא $\omega L \!\$ .

חשוב לציין שהאימפדנס של קבל או סליל תלוי בתדירות $\omega \!\$ והוא גודל מדומה, אבל מהווה תופעה פיזיקלית אמיתית של הפרש פאזה בין הפאזורים של המתח והזרם כתוצאה מנוכחות הקבל או הסליל. לעומת זאת האימפדנס של הנגד הוא קבוע וממשי חיובי, ולכן אינו גורם להפרש פאזה בין הפאזורים של המתח והזרם.

כאשר נגדים, קבלים וסלילים משולבים במעגל AC, ניתן לחבר את האימפדנסים של הרכיבים באותו אופן שמחברים התנגדויות במעגל DC. האימפדנס השקול המתקבל הוא באופן כללי גודל מרוכב, כלומר יש לו חלק ממשי וחלק מדומה. מסמנים את האימפדנס השקול באופן הבא:

$Z_\mathrm{eq} = R_\mathrm{eq} + jX_\mathrm{eq} \!\$

כאשר:

$R_\mathrm{eq} \!\$ נקרא החלק ההתנגדותי של האימפדנס.

$X_\mathrm{eq} \!\$ נקרא החלק הריאקטיבי של האימפדנס.

מקובל להתייחס לקבל או לסליל כרכיב ריאקטיבי. האימפדנס של קבל הוא מדומה שלילי בעוד שהאימפדנס של סליל הוא מדומה חיובי. רכיב ריאקטיבי צורך אנרגיה מהמעגל ומחזיר אנרגיה למעגל לחילופין, ולכן בניגוד לנגד אינו צורך הספק.

ניתן לקבוע את התנהגותו של הקבל בתדירויות קיצוניות. כשהתדירות מתקרבת לאפס, הריאקטנס של הקבל גדל ללא גבול כך שהקבל מתנהג כמו נתק במעגל העובד בתדירויות נמוכות מאוד של מקורות סינוסיים. ככל שהתדירות גדלה, הריאקטנס של הקבל מתקרב לאפס כך שהקבל מתנהג כמו קצר במעגל העובד בתדירויות גבוהות מאוד של מקורות סינוסיים.

לעומת זאת, התנהגותו של הסליל הפוכה בתדירויות קיצוניות. כשהתדירות מתקרבת לאפס, הריאקטנס של הסליל מתקרב לאפס כך שהסליל מתנהג כמו קצר במעגל העובד בתדירויות נמוכות מאוד של מקורות סינוסיים. ככל שהתדירות גדלה, הריאקטנס של הסליל גדל ללא גבול כך שהסליל מתנהג כמו נתק במעגל העובד בתדירויות גבוהות מאוד של מקורות סינוסיים.

[עריכה] חיבור אימפדנסים

חיבור אימפדנסים בטור או במקביל הוא כמו בנגדים, כשההבדל הוא שבחיבור אימפדנסים יש לטפל במספרים מרוכבים.

[עריכה] בטור

חיבור אימפדנסים בטור הוא פשוט:

$Z_\mathrm{eq} = Z_1 + Z_2 = (R_1 + R_2) + j(X_1 + X_2) \!\$

[עריכה] במקביל

חיבור אימפדנסים במקביל מסובך בהרבה מחיבור תכונות פשוטות כמו התנגדות או קיבול עקב גורם המכפלה.

$Z_\mathrm{eq} = Z_1 \| Z_2 = \left( {Z_\mathrm{1}}^{-1} + {Z_\mathrm{2}}^{-1}\right) ^{-1} = \frac{Z_\mathrm{1}Z_\mathrm{2}}{Z_\mathrm{1}+Z_\mathrm{2}} \!\$

האימפדנס המתקבל הוא: $Z_\mathrm{eq} = R_\mathrm{eq} + j X_\mathrm{eq} \!\$
כאשר:

$R_\mathrm{eq} = { (X_1 R_2 + X_2 R_1) (X_1 + X_2) + (R_1 R_2 - X_1 X_2) (R_1 + R_2) \over (R_1 + R_2)^2 + (X_1 + X_2)^2}$

$X_\mathrm{eq} = {(X_1 R_2 + X_2 R_1) (R_1 + R_2) - (R_1 R_2 - X_1 X_2) (X_1 + X_2) \over (R_1 + R_2)^2 + (X_1 + X_2)^2}$

[עריכה] מעגלים עם מקורות כלליים

אימפדנס מוגדר על ידי היחס בין שני פאזורים כשפאזור מוגדר על פונקציה סינוסית של הזמן. עבור מקורות מחזוריים כלליים ואפילו מקורות לא מחזוריים, עדיין ניתן להשתמש במושג האימפדנס. ניתן להראות שכמעט כל הפונקציות המחזוריות בזמן ניתנות לייצוג על ידי טור פורייה. לכן, ניתן לחשוב על מקור מתח מחזורי כלשהו כקומבינציה (אולי אינסופית) של מקורות מתח סינוסיים בטור. באופן דומה, ניתן לחשוב על מקור זרם מחזורי כלשהו כקומבינציה (אולי אינסופית) של מקורות זרם סינוסיים במקביל.

תוך שימוש בשיטת הסופרפוזיציה, כל מקור מופעל בנפרד ומוצאים פתרון של מעגל ה-AC בעזרת האימפדנסים המחושבים עבור התדירות של המקור המופעל. הפתרונות של המתחים והזרמים של המקור שהופיע במעגל המקורי מחושבים כסכומים של הפתרונות שחושבו לכל אחד מהמקורות המרכיבים אותו. עם זאת חשוב לציין שלמתחים ולזרמים האמיתיים במעגל המקורי אין ייצוג פאזורי. ניתן לחבר פאזורים רק כאשר כל אחד מהם מייצג פונקציה בזמן בעלת אותה תדירות. לכן, יש להחזיר את פאזורי המתח והזרם שחושבו עבור כל מקור בנפרד לייצוג שלהם בתחום הזמן לפני ביצוע הסכימה הסופית.

שיטה זו ניתנת להכללה למקורות לא מחזוריים כאשר את הסכומים הבדידים מחליפים אינטגרלים. כלומר, את טור פורייה מחליפה התמרת פורייה.

[עריכה] גודל ופאזה של אימפדנס

מספרים מרוכבים מיוצגים בדרך כלל בשתי צורות. ההצגה הקרטזית היא פשוט הסכום של החלק הממשי עם מכפלת החלק המדומה ב- $j$ :

$Z = R + jX \!\$

ההצגה הקוטבית של מספר מרוכב היא הגודל הממשי של המספר מוכפל בפאזה המרוכבת. ניתן לכתוב זאת בעזרת אקספוננט, או בייצוג פאזורי:

$Z = \left|Z\right| e^ {j \varphi} = \left|Z\right|\angle \varphi$

כאשר:

$\left|Z\right| = \sqrt{R^2+X^2} = \sqrt{Z Z^*}$ הוא הגודל של $Z \!\$ ( $Z^* \!\$ מציין את הצמוד המרוכב של $Z \!\$ )

$\varphi = \arctan \bigg(\frac{X}{R} \bigg)$ היא הזווית

[עריכה] פאזור שיא מול פאזור שורש הממוצע הריבועי

למתח או זרם סינוסי יש ערך שיא של האמפליטודה ובנוסף ערך rms (שורש הממוצע הריבועי). ניתן להראות שערך ה-rms של המתח או הזרם הסינוסי נתון על ידי:

$V_\mathrm{rms} = \frac{V_\mathrm{peak}}{\sqrt{2}}$

$I_\mathrm{rms} = \frac{I_\mathrm{peak}}{\sqrt{2}}$

במקרים רבים של ניתוח AC, ערך ה-rms של סינוסואידה מועיל יותר מאשר ערך השיא. לדוגמה, לקביעת כמות ההספק הנצרך על ידי נגד שזורם דרכו זרם סינוסי, יש לדעת את ערך ה-rms של הזרם. מסיבה זו, לעתים מציינים את פאזורי ה-rms של מקורות מתח וזרם סינוסיים במקום את פאזורי השיא. באופן כללי משתמשים בפאזורי rms בהנדסת הספק חשמלי בעוד שמשתמשים בפאזורי שיא בניתוח מעגלים בעלי הספק נמוך.

בכל מקרה, האימפדנס יהיה זהה לכל בחירה של פאזור. בין אם משתמשים בפאזורי שיא או rms, הגורם הקבוע שמבדיל בין הפאזורים מתבטל כאשר נלקח היחס בין הפאזורים.

[עריכה] ראו גם

[עריכה] קישורים חיצוניים

הסבר על אימפדנס (אנגלית)

[עריכה] מקורות

Pohl R. W., Electrizitätslehre, Berlin-Göttingen-Heidelberg: Springer-Verlag, 1960
Popov V. P., The Principles of Theory of Circuits, – M.: Higher School, 1985, 496 p (רוסית)
Küpfmüller K., Einführung in die theoretische Elektrotechnik, Springer-Verlag, 1959

חשמל
מושגי יסוד	שדה חשמלי • מתח חשמלי • זרם חשמלי • התנגדות ומוליכות • עכבה • הספק חשמלי • קיבול חשמלי • השראות • זרם ישר • זרם חילופין • חוק אוהם • מעגל חשמלי • אנרגיה חשמלית • מעגל תהודה חשמלי • מעגל RLC
רכיבים בסיסים	מוליך • מבודד • מקור מתח • מקור זרם • סוללה • נגד • קבל • משרן • שנאי • מתג
מכשירי מדידה	אוסצילוסקופ • אמפרמטר • אוהם-מטר • גלוונומטר • וולטמטר • רב מודד • מד השראות • מד קיבול
אלקטרוניקה	מוליך למחצה • דיודה • טרנזיסטור • טריודה • מעגל משולב • מעגל מודפס • שפופרת ריק • מיקרואלקטרוניקה
יחידות מידה	וולט • אמפר • פאראד • אוהם • ואט • קולון • הנרי • סימנס • ואט-שעה • ג'ול
זרם חזק	גנרטור חשמלי • מנוע חשמלי • תחנת כוח • מערכת חלוקה
בטיחות בחשמל	התחשמלות • לוח חשמל • ממסר פחת • מאמ"ת • נתיך • הארקה • קצר חשמלי

עכבה חשמלית

מתוך ויקיפדיה, האנציקלופדיה החופשית

תוכן עניינים

[עריכה] מצב מתמיד סינוסי

[עריכה] הגדרה וסימון האימפדנס החשמלי

[עריכה] אימפדנס של רכיבים

[עריכה] היגב

[עריכה] חיבור אימפדנסים

[עריכה] בטור

[עריכה] במקביל

[עריכה] מעגלים עם מקורות כלליים

[עריכה] גודל ופאזה של אימפדנס

[עריכה] פאזור שיא מול פאזור שורש הממוצע הריבועי

[עריכה] ראו גם

[עריכה] קישורים חיצוניים

[עריכה] מקורות

צפיות

כלים אישיים

ניווט

קהילה

חיפוש

תיבת כלים

שפות אחרות