חוקי פרנל

חוקי פרנל הם כללים פיזיקליים המתארים כיצד גל אלקטרומגנטי ובפרט אור, מוחזר ונשבר במפגש בין שני חומרים בעלי תכונות אופטיות שונות, כגון זכוכית ואוויר. החוקים נקראים על שם אוגוסטן ז'אן פרנל אשר הגה אותם ברבע הראשון של המאה ה-19. חוקים אלו הם מעמודי התווך של האופטיקה ומשמשים כבסיס להסבר תופעות אופטיות רבות כגון, החזרה פנימית מלאה, זווית ברוסטר, התאבכות משכבות והקיטובים של אופנים מולכים.

היסטוריה[עריכת קוד מקור | עריכה]
חוקי פרנל באו כ-200 שנה אחרי שהריוט, סנל ודקארט גילו את חוקי ההחזרה והשבירה לעולם האירופאי. פרנל עשה את הצעד הבא כאשר בעזרת חוקיו, תיאר לא רק את הכיוון אליו האור יוחזר ויישבר, אלא גם את חלוקת העוצמה של הגל הפוגע בין הגל הנשבר והמוחזר. המרכיבים החסרים ב-200 שנה אלו היו הבנת הקיטוב של האור, ותכונותיו הגליות. אף על פי שבעזרת גבישי קלציט איסלנדי כבר בשנות ה-70 של המאה ה-17 ידעו הויגנס וברתולין שלאור השמש קיימת תכונה חבויה לה קראו קיטוב, אף אחד לא ידע לתאר פיזיקלית את מקור תכונת הקיטוב. בנוסף לכך העולם המדעי במאה ה-18 קבל כמעט באופן מוחלט את תפיסתו של ניוטון בה האור הוא זרם חלקיקים, על פני התפיסה הגלית של הויגנס. פרנל ויאנג גילו באופן בלתי תלוי גם את תכונותיו הגליות של האור בניסויים שונים של התאבכות, וגם את קיטובו הרוחבי של אור השמש[1]. חוקי פרנל הם תלויים בכיוון התנודות של הגל האלקטרומגנטי (דהיינו הקיטוב), לתנודות אלו אין מקום בתורה החלקיקית של ניוטון. פרנל בחייו הקצרים הבין את תכונותיו הגליות של האור ביניהן הקיטוב, ועם הבנה זאת ידע לפתח את חוקי פרנל מתאוריה מכנית של ויברציות בחומר. כיום מקובל להוכיח את חוקי פרנל תאורטית ממשוואות מקסוול אשר נולדו לעולם רק כמחצית המאה לאחר מכן.
הסבר[עריכת קוד מקור | עריכה]
כאשר גל אלקטרומגנטי הנע בחומר בעל מקדם שבירה פוגע בזווית כניסה בגבול של חומר שני בעל מקדם שבירה , חלקו מוחזר בזווית שווה לזווית הפגיעה וחלקו נשבר על פי חוק סנל (ראו איור 1). מתמטית ניתן לרשום את הגל בתווך הראשון כסכום של הגל הפוגע והגל המוחזר.

כאשר מסמן את פעולת ההחזרה אשר יכולה לשנות את המשרעת, מופע וקיטוב של השדה החשמלי הפוגע .
בתווך השני קיים רק הגל הנשבר.
כאשר מסמן את פעולת השבירה.
חוקי פרנל מתארים כמותית את פעולת ההחזרה והשבירה על מנת שיהיה ניתן לחשב את המשרעת, המופע והקיטוב של הגל המוחזר והנשבר ביחס לגל הפוגע. לדוגמה כאשר אור הנע באוויר פוגע בניצב במשטח זכוכית 4% מהעוצמה תוחזר והקיטוב יהיה זהה לקיטוב של האור הפוגע (בגלל הפגיעה המאונכת). מתמטית חוקים אלו מגולמים במשוואות פרנל אשר מחשבים את מקדמי ההחזרה והשבירה כתלות במשתנים הבאים:
- מקדם השבירה של שני החומרים
- הקיטוב
- זווית הפגיעה
משוואות פרנל מתארות את ההחזרה והשבירה של גל מישורי על ידי משטח אינסופי שטוח ואחיד. בפועל משוואות פרנל נותנות תוצאות שימושיות ברמת דיוק גבוהה עבור קרני אור מקבילות אשר פוגעות במשטח הגדול מכתם האור ושטוח ביחס לאורך הגל של האור. בערך זה נתאר את השדה החשמלי של הגל רק כגל מישורי אידיאלי, כלומר גל בעל קיטוב רוחבי.
קיטוב[עריכת קוד מקור | עריכה]
כאשר גל אלקטרומגנטי פוגע במבנה של שכבות אחידות ואיזוטרופיות (בפרט תווך של שני חומרים המתואר בחוקי פרנל) קיימים שני קיטובים עצמיים של המבנה, קיטוב ניצב למישור הפגיעה (אנ') (מישור הנפרש על ידי וקטור כיוון התקדמות הגל והווקטור הניצב למשטח) הידוע כקיטוב 's', וקיטוב מקביל למישור הפגיעה הידוע כקיטוב 'p'. אור המקוטב בקיטובים אלו לא ישנה את קיטובו בהחזרה ובשבירה. מקדמי ההחזרה וההעברה של משוואות פרנל כתובים בנפרד לכל קיטוב עצמי. על מנת לחשב את ההחזר עבור קיטוב כללי יש צורך לפרקו בבסיס של הקיטובים העצמיים, לחשב את ההחזרה/שבירה של השדה החשמלי לכל קיטוב בנפרד על פי משוואות פרנל ולחברם בחזרה. לדוגמה אם הגל הנכנס הוא בעל קיטוב מעגלי ימני .
כאשר הם ווקטורי היחידה בכיוון הקיטוב הניצב ובכיוון הקיטוב במקביל אזי הקיטוב בהחזרה יהיה,
ובדומה הקיטוב הנשבר יהיה
כאשר ו הם מקדמי ההחזרה והשבירה של משוואות פרנל בהתאמה עבור הקיטובים העצמיים השונים.
ניתן לראות שהקיטוב יהפוך לקיטוב אליפטי לאחר ההחזרה/העברה עבור כל זווית פגיעה השונה מאפס. זאת מכיוון שעל פי חוקי פרנל המשרעת של הגל החוזר אינה שווה עבור שני הקיטובים העצמיים בכל זווית פרט לפגיעה ניצבת או פגיעה שטוחה . בסביבת שני מצבי קצה אלו ההחזר והשבירה בקירוב טוב, אינם תלוים בקיטוב של הגל הפוגע, ולפיכך כל קיטוב הוא קיטוב עצמי של המבנה בזוויות אלו.
זווית ברוסטר[עריכת קוד מקור | עריכה]
ניתן להראות ממשוואות פרנל עבור מקדם ההחזרה של הקיטוב המקביל () שבכל מעבר תווך דיאלקטרי חייב המקדם להתאפס בזווית כלשהי. זווית זו נקראת זווית ברוסטר על שם הפיזיקאי דייוויד ברוסטר שגילה אותה, האור המוחזר במקרה זה יהיה מקוטב בקיטוב מאונך () ועל כן ברוסטר קרא לזווית, זווית הקיטוב. ברוסטר גילה את זווית הקיטוב באופן ניסיוני כעשור לפני שפרנל פיתח את משוואותיו. קיימים חומרים כיראלים (לא ניתן לתארם רק בעזרת אינדקס שבירה) בהם קיימת זווית קיטוב אך עוצמת ההחזר () אינה יורדת לאפס.
המשוואות (סימונים שונים)[עריכת קוד מקור | עריכה]
קיימות גרסאות רבות למשוואות פרנל. נביא כאן כמה מהגישות מספרי אופטיקה נפוצים המתארים את מקדמי ההחזרה והעברה של השדה החשמלי (למשל Born & Wolf), העוצמה () ושטף העוצמה (למשל Siegmann). כל המשוואות הן עבור חומרים ליניארים איזוטרופים ללא תגובה מגנטית.
שדה חשמלי[עריכת קוד מקור | עריכה]
המשוואות עבור מקדמי ההחזרה וההעברה לשדה החשמלי הן (מחוק סנל + תנאי שפה על השדה החשמלי והמגנטי) :
כאשר הוא היחס בין מקדם השבירה בשני החומרים, היא ההגדלה האופטית.
כמו כן, מקדמי ההעברה תלויים במקדמי ההחזרה לפי:
משוואות פרנל אינן תלויות ישירות באורך הגל אלא רק בזווית הכניסה ובחומרים, התלות באורך הגל של האור היא רק דרך הנפיצה של החומר.
עוצמת השדה[עריכת קוד מקור | עריכה]
עוצמת השדה החשמלי מוגדרת כ , ולכן המשוואות עבור מקדמי ההחזרה והעברה הן בפשטות ו . בניגוד למשוואות השדה משוואות העוצמה אינן תלויות בבחירת מערכות הצירים בהעברה והחזרה בגלל שהבדלי הסימן נעלמים כאשר מעלים את השדה בריבוע:
להלן דוגמה של מקדמי ההחזרה (עוצמת השדה) עבור הקיטובים השונים במעבר בין תווך דיאלקטרי בעל מקדם שבירה לתווך דיאלקטרי בעל מקדם שבירה .
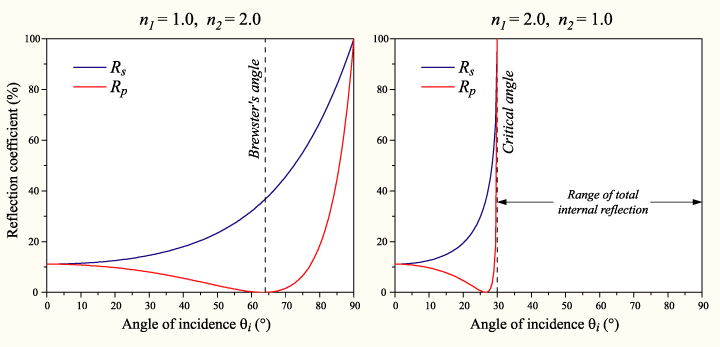
שטף האנרגיה[עריכת קוד מקור | עריכה]
בבעיות פיזור של אור קיים חוק שימור של שטף העוצמה. כלומר שטף האנרגיה הנכנס שווה לשטף האנרגיה היוצא. במקרה של חוקי פרנל פיזור במפגש של שני תווכים אחידים אופטית, השטף היוצא הוא סכום שטף האנרגיה המוחזר והנשבר. מתמטית הדבר זהה לחוק שימור זרם ההסתברות במכניקת הקוונטים. שטף האנרגיה תלוי בעוצמה אך גם תלוי במהירות הגל בחומר ובזווית התקדמותו יחסית למפזר.
שטף העוצמה החשמלית היא האנרגיה ליחידת זמן החוצה במאונך את המפגש בין שני התווכים ולכן מוגדר כ: , ולכן המשוואות עבור מקדמי ההחזריות והמעבריות הם: ו . על פי חוק שימור שטף העוצמה .
הפרש המופע בהחזרה ושבירה[עריכת קוד מקור | עריכה]
משוואות פרנל עבור השדה החשמלי (בניגוד לעוצמה החשמלית) המוחזר והמועבר מתארות את השינוי במשרעת והפרש המופע של הגל המוחזר והנשבר ביחס לגל הפוגע. תכונה זאת של הפרש מופע אינה מופיעה ברבים מספרי האופטיקה, ניתן להמחיש אותה בסימולציה בראש ערך זה בה הגל המוחזר מקבל היפוך מופע ולמועבר אין הפרש מופע.
בהנחה שהאור הפוגע מקוטב ליניארית בקיטוב כללי הכולל גם s וגם p, אזי כל הבדל בין מקדמי פרנל עבור הקיטובים השונים יגרום להפיכת הקיטוב לאליפטי. הפרש המופע של קיטובי s ו p שונה עבור אור בהחזרה מלאה. תכונה זאת אפשרה לפרנל להנדס כבר לפני 200 שנה את מעוין פרנל אשר הופך קיטוב ליניארי/מעגלי לקיטוב מעגלי/ליניארי.
ניתן לסכם את הפרשי המופע של מקדמי פרנל עבור מעבר בין שני חומרים דיאלקטרים איזוטרופים כדלקמן:[2](הקישור אינו פעיל)
- במעבר בין תווך בעל מקדם שבירה נמוך למקדם שבירה גבוה;
- אין הפרש מופע של הגל הנשבר ביחס לגל הפוגע.
- לקיטוב s יש היפוך מופע בהחזרה ביחס לגל הפוגע.
- לקיטוב p אין היפוך מופע בהחזרה עבור גל נכנס בזווית פגיעה קטנה מזווית ברוסטר ויש היפוך מופע עבור זווית גדולה מזווית ברוסטר.
אזהרה, הפרשי המופע תלויי הגדרה, ניתן למצוא הגדרות בהן היפוך המופע לקיטוב p בהחזרה הוא עד ברוסטר, ואין היפוך מעבר לברוסטר. מה שאינו תלוי הגדרה הוא שהפרש המופע כתלות בזווית הכניסה רציף לקיטוב s ובעל קפיצה של (היפוך מופע) בזווית ברוסטר עבור קיטוב p.
- במעבר בין תווך בעל מקדם שבירה גבוה למקדם שבירה נמוך;
- אין הפרש מופע של הגל הנשבר ביחס לגל הפוגע עד לזווית הקריטית של החזרה מלאה.
- לקיטוב s אין היפוך מופע בהחזרה ביחס לגל הפוגע עד לזווית הקריטית.
- לקיטוב p יש היפוך מופע בהחזרה עבור גל נכנס בזווית פגיעה קטנה מזווית ברוסטר ואין היפוך מופע עבור זווית גדולה מזווית ברוסטר וקטנה מהזווית הקריטית.
- עבור זוויות גדולות מהזווית הקריטית, הפרש המופע ביחס לגל הפוגע יורד באופן מונוטוני עבור שני הקיטובים. ההפרש בין הפרשי המופע של שני הקיטובים הוא בזווית הקריטית ובגבול של פגיעה אופקית, בזוויות פגיעה בין שני מקרי הקצה, הערך המוחלט של הפרש הפאזה של קיטוב p תמיד יהיה יותר גדול מזה של קיטוב s. השוני בין שני הקיטובים יהיה יותר גדול ככל ש q (היחס בין מקדם השבירה הנמוך לגבוה) יהיה יותר קטן (ראו דוגמה באיור 2).

דוגמה להשפעה של המופע בהחזרה מלאה באופטיקה היא עקומות הנפיצה של אופנים מולכים במוליך גלים. אופני תנודה אלו הם בעלי קיטוב TE/TM, גלים אלו לכודים בתוך המוליך על ידי החזרה מלאה, אך הם יכולים להתקיים באופן יציב רק כאשר הם מתאבכים באופן בונה עם עצמם. תנאי ההתאבכות הבונה הוא:
כאשר הוא הרכיב הניצב למשטח של וקטור ההתקדמות של הגל בטווח, הוא רוחב מוליך הגלים ו הוא הפרש המופע בהחזרה במפגש בין טווח מוליך הגלים לתווך מצד אחד או מצד שני ו הוא סדר האופן המולך (כלומר כמה פעמים השדה מתאפס לאורך חתך של מוליך הגלים). וקטור ההתקדמות אינו תלוי בקיטוב, אך הפרש המופע בהחזרה שונה עבור קיטובי s ו p, ולפיכך תנאי ההולכה שונה לאופנים בעלי קיטוב s (אופני TE) ולאופנים בעלי קיטוב p (אופני TM), מה שמסביר את ההבדל ביחס הנפיצה.
פיתוח[עריכת קוד מקור | עריכה]
פרנל פיתח את חוקיו ממודל מכני של תגובת החומר לאור, אך כיום מקובל לפתח את החוקים ישירות ממשוואות מקסוול תחת ההנחה של תגובה ליניארית ותווך ללא זרמים ומטענים חופשיים.
תנאי שפה[עריכת קוד מקור | עריכה]
בעזרת חוק גאוס ניתן להראות ש:
- הרכיב המקביל למישור הפגיעה של שדה ההשראות החשמלית D רציף כלומר קיימת אי רציפות לרכיב השדה החשמלי הניצב התלויה במקדם דיאלקטרי של החומר
- בהינתן שאין מטענים חופשיים הרכיב הניצב של שדה ההשראות המגנטי B רציף
בעזרת משפט סטוקס ניתן להראות ש:
- הרכיב הרוחבי של השדה החשמלי E רציף
- בהינתן שאין זרמים הרכיב הרוחבי של השדה המגנטי H רציף
בהנחה שאין תגובה מגנטית לחומר, כלומר (דבר הנכון לחומרים ידועים בתחום האור הנראה), ניתן להראות שדרישות תנאי השפה הרוחביות עבור שדה חשמלי ומגנטי של גל מישורי המוחזר ונשבר על פי הזוויות של חוק ההחזרה וחוק סנל, חייב לקיים את ארבע המשוואות הבאות.
הרחבה לחומרים אחרים[עריכת קוד מקור | עריכה]
בנוסף למעבר בין שני תווכים דיאלקטרים איזוטרופים, ללא תגובה מגנטית, ניתן להרחיב את חוקי פרנל לתווכים אחרים, כאשר ההתייחסות תמיד היא למעבר מחומר דיאלקטרי כגון אוויר לתווך בעל החומר המדובר.
תגובה מגנטית[עריכת קוד מקור | עריכה]
המשוואות ניתנו עבור חומרים ללא תגובה מגנטית ().
גבישי שבירה כפולה[עריכת קוד מקור | עריכה]
פרנל עצמו כמו חוקרים רבים בזמנו חקרו את תכונת הקיטוב של האור בגבישי שבירה כפולה, בפרט קלציט. באופן כללי גבישים אשר אינדקס השבירה שלהם אינו אחיד לכיוון ההתקדמות של הגל האלקטרומגנטי אינם מקיימים את תכונת הקיטוב העצמי של קיטובי s ו-p, זאת משום שהקיטוב הרגיל והבלתי רגיל נעים בכיוונים שונים בתוך הגביש.
שימושים[עריכת קוד מקור | עריכה]
- גרפיקה ממוחשבת כיום כאשר מעוניינים ליצור תמונות מציאותיות במשחקי מחשב או יישומים אחרים יש דגש רב על משחקי אור צל והשתקפויות. משוואות פרנל הן הבסיס לחישוב עוצמת האור שמוחזרת ונשברת בפגיעה בעצמים חלקים, כגון כדורי זכוכית
- התגובה האופטית של רכיבים אופטיים בעלי שכבות רבות כגון מראות דיאלקטריות ומפצלי אלומה תלויה בעובי של כל שכבה ובמקדמי פרנל בין השכבות. התגובה האופטית היא התאבכות כל המסלולים האופטיים האפשריים בין השכבות. בעזרת משוואות פרנל ניתן לחשב את התגובה האופטית. לעיתים שיטה כזאת עוזרת בתכנון רכיב אשר ייתן תגובה רצויה מכיוון שניתן להבין מה "תפקידה" של כל שכבה, כגון ציפוי אל החזר
- מעוין פרנל
- partial reflectors
- לייזרים מקוטבים בעזרת מראה חלקית המוצבת בזווית ברוסטר בתוך המהוד של הלייזר





































![{\displaystyle R_{s}=\left[{\frac {\sin(\theta _{t}-\theta _{i})}{\sin(\theta _{t}+\theta _{i})}}\right]^{2}=\left({\frac {n_{1}\cos \theta _{i}-n_{2}\cos \theta _{t}}{n_{1}\cos \theta _{i}+n_{2}\cos \theta _{t}}}\right)^{2}=\left[{\frac {n_{1}\cos \theta _{i}-n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}}{n_{1}\cos \theta _{i}+n_{2}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b92746c5ddf76cd0560b4798438aa7efc04f009)
![{\displaystyle R_{p}=\left[{\frac {\tan(\theta _{t}-\theta _{i})}{\tan(\theta _{t}+\theta _{i})}}\right]^{2}=\left({\frac {n_{1}\cos \theta _{t}-n_{2}\cos \theta _{i}}{n_{1}\cos \theta _{t}+n_{2}\cos \theta _{i}}}\right)^{2}=\left[{\frac {n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}-n_{2}\cos \theta _{i}}{n_{1}{\sqrt {1-\left({\frac {n_{1}}{n_{2}}}\sin \theta _{i}\right)^{2}}}+n_{2}\cos \theta _{i}}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/269fc0d8deb5f59f0349c28ad15504fc8ed44aff)













