שדה מגנטי

שדה מגנטי, הוא תכונה של המרחב סביב זרם חשמלי או חומר מגנטי, המפעילה כוח על מגנטים וזרמים חשמליים. במילים אחרות, השדה המגנטי הוא ביטוי לכוח שמפעילים זרמים חשמליים או חומרים מגנטיים זה על זה. השדה נמדד ביחידות טסלה (T) במערכת היחידות הבינלאומית.
השדה המגנטי הוא שדה וקטורי, ובכך מתאים וקטור לכל נקודה במרחב, ומתואר באיורים על ידי קווי שדה. קווים אלה מתארים את הכיוון אליו תצביע מחט של מצפן בכל נקודה במרחב.
היחידה הבסיסית ביותר אשר מפיקה שדה מגנטי היא דיפול מגנטי, שהוא חלקיק בעל שני קטבים מגנטיים מנוגדים צמודים. דיפול מגנטי יכול להיות קטע מתיל עם זרם חשמלי, חלקיק טעון בתנועה, או חלקיק טעון בעל תנע זוויתי עצמי. ההשפעה של שדה מגנטי על גוף מוליך זרם תלויה בכיוון הזרם ביחס לכיוון השדה. אם כיוון הזרם מקביל לכיוון השדה, לא תהיה השפעה כלל, ואם כיוון הזרם אנך לכיוון השדה ההשפעה תהיה מקסימלית.
תופעת המגנטיות, כמשיכה ודחייה בין אבנים, מוכרת מזה אלפי שנים. שימוש במצפן למציאת הצפון באמצעות השדה המגנטי של כדור הארץ מוכר מזה כאלפיים שנה[1][2].
הנס כריסטיאן ארסטד גילה בשנת 1820 שזרם חשמלי יוצר שדות מגנטיים.
השדה המגנטי קשור באופן הדוק לשדה חשמלי, וניתן לחשב את הכח המגנטי שיוצר חלקיק טעון חשמלית בתנועה (המהווה זרם חשמלי), מתוך השדה של מטען חשמלי והדרישה לשימור המטען במעבר בין מערכות ייחוס יחסותיות. מעבר כזה נקרא טרנספורמציית לורנץ. המשוואות אשר קושרות בין שדה מגנטי לחשמלי נקראות משוואות מקסוול.
היסטוריה[עריכת קוד מקור | עריכה]
מגנטיות ככוח בין חומרים מגנטיים ידועה כבר מימי קדם. במאה ה-19 נחקר הקשר בין חשמל ומגנטיות, והוכלל לתורה אחת, תורת האלקטרומגנטיות, עם המשוואות היסודיות של התורה שהן משוואות מקסוול. בראשית המאה ה-20 באמצעות תורת היחסות הפרטית פותחה תורה שלמה ועקבית המוכללת במשוואות מקסוול בצורה יחסותית.
שדות וכוחות מגנטיים יסודיים[עריכת קוד מקור | עריכה]
מבוא מתמטי[עריכת קוד מקור | עריכה]
לחישוב ערכם של שדות מגנטיים והכח שהם מפעילים, נדרשת פעולה מתמטית שנקראת מכפלה וקטורית, המסומנת כ-. מכפלה וקטורית מתבצעת בין שני וקטורים והתוצאה שלה היא וקטור.
תוצאת המכפלה תהיה הווקטור , כאשר:
גודל הווקטור, , הוא ערכה של המכפלה,
- ,
וכיוונו ניצב לכיוונם של שני הווקטורים, ונקבע על פי כלל יד ימין (להרחבה על הסימונים ראו וקטור).
חלקיק נע בעל מטען חשמלי[עריכת קוד מקור | עריכה]

השדה המגנטי בנקודה מסוימת שיוצר מטען נע (וגם זרם חשמלי) נקבע על פי חוק ביו-סבר. השדה יחסי לגודל המטען ומהירותו ויחסי להיפוך ריבוע המרחק בין המטען לנקודה שבה השדה נמדד. השדה ניצב לכיוון תנועת המטען ולקו (הווקטור) בין המטען לנקודה. קווי השדה המגנטי מסודרים במעגלים הולכים וגדלים סביב למסלול המטען היוצר אותו ומכוונים לפי כלל יד ימין (ראו איור).
בניסוח מתמטי, השדה המגנטי שיוצר חלקיק בעל מטען חשמלי הנע במהירות , בנקודה שנמצאת במיקום במרחב ביחס לחלקיק, הוא:
כאשר הוא מקדם המגנטיות של הריק, שערכו .
באופן דומה עבור תיל קצר באורך וכיוון עם זרם חשמלי :

הכוח שמפעיל שדה מגנטי על חלקיק טעון נע נקרא כוח לורנץ. הכוח ניצב למהירות החלקיק הטעון ולשדה המגנטי שיצר אותו. כאשר חלקיק טעון נע בשדה מגנטי קבוע ואחיד, הוא נע במסלול לולייני שבו ציר הסליל מקביל לשדה המגנטי וגודל מהירות החלקיק נשאר קבוע. מכיוון שהכוח המגנטי תמיד מאונך לתנועה, הוא לא מבצע עבודה על חלקיק טעון ובודד במרחב. בעקיפין יכול השדה המגנטי לעשות עבודה באמצעות השדה החשמלי שנוצר כתוצאה משדה מגנטי משתנה. בניסוח מתמטי, הכוח שמפעיל שדה מגנטי על מטען שנע במהירות הוא:
- .
מקרה פרטי של נוסחה זו הוא הכוח שפועל על קטע תיל קצר באורך וכיוון עם זרם :
- .
דיפול מגנטי[עריכת קוד מקור | עריכה]
דיפול מגנטי הוא זוג מטענים מגנטיים מנוגדים צמודים (צפון-דרום), והוא יחידה בסיסית היוצרת שדה מגנטי. לא נמצא עד כה בניסוי מטען מגנטי בודד (מונופול מגנטי) וחיפוש אחר חלקיק זה הוא אחד מתחומי המחקר של פיזיקת חלקיקים. מציאתו תסביר תופעות כמו, למשל, קוונטיזציה של המטען החשמלי ביקום. הגודל המאפיין את חוזק המגנט הוא המומנט המגנטי , וקטור שכוונו הציר שבין המטענים, מהמטען החיובי לשלילי.
השדה שיוצר דיפול מגנטי מתואר באיור. באופן מתמטי, השדה הוא:
דיפול מגנטי יכול להיות גם מתואר באמצעות לולאת זרם:
כאשר הוא שטח הלולאה, הוא כיוון מומנט הדיפול שניצב לשטח הלולאה על פי כלל יד ימין, ו- הוא הזרם בלולאה.
שדה מגנטי אחיד לא יפעיל על הדיפול כוח כולל, אולם יפעיל עליו מומנט כוח:
- .
שדה מגנטי ושדה חשמלי[עריכת קוד מקור | עריכה]
הנוסחאות הבסיסיות שהוצגו בעייתיות, מאחר שלא מוגדרת בהן מערכת ייחוס. בנוסחת כח לורנץ, למשל, המהירות אינה מוגדרת היטב, וניתן לראות שבחירת מערכת ייחוס הנעה במהירות שונה משנה את הכח שפועל על החלקיק, תוצאה שאינה פיזיקלית שכן בשתי מערכות הייחוס נמדדת אותה תאוצה. סתירה זו נפתרת באמצעות תורת היחסות הפרטית שמאחדת את השדה המגנטי עם השדה החשמלי לגודל פיזיקלי הנקרא טנזור השדה האלקטרומגנטי. למעשה, אפשר לקבל את השדה המגנטי מהשדה חשמלי, ולהפך, על ידי טרנספורמציית לורנץ, שהיא מעבר מערכת ייחוס בתורת היחסות.
השדה המגנטי והפוטנציאל הווקטורי[עריכת קוד מקור | עריכה]
שדה מגנטי נייח מקיים את שתי משוואות מקסוול הבאות (עוד שתיים אינן מוצגות כאן):
המשוואה הראשונה נכונה כל עוד אין במערכת מונופולים מגנטיים (ולא התגלו כאלו עד כה), כלומר כל חלקיק מגנטי הוא דיפול בעל קוטב צפוני ודרומי. מכיוון שלכל שדה וקטורי מתקיים , ניתן להציג את השדה באמצעות פוטנציאל וקטורי , על ידי:
מן הפוטנציאל הווקטורי גוזרים את השדה המגנטי, כפי שמהפוטנציאל החשמלי גוזרים את השדה החשמלי.
משמעות המשוואה השנייה היא ששדות מגנטים נייחים נוצרים רק מזרמים חשמליים ושכיוון השדה הוא מסביב לתנועת הזרם. צורה זו של המשוואה איננה מדויקת, כי כאשר שדה חשמלי משתנה בזמן, הוא משרה שדה מגנטי בסביבתו, בדיוק כמו זרם חשמלי. הצורה המתוקנת של המשוואה השנייה על פי מקסוול היא:
הנגזרת של השדה החשמלי לפי הזמן נקראת זרם העתקה, בהתאם לתפקידה כמקור של שדה מגנטי.
באופן דומה, שדה מגנטי משתנה בזמן יוצר שדה חשמלי והקשר ביניהם ניתן על ידי משוואת מקסוול נוספת (חוק פאראדיי):
שתי משוואות אלה מתארות את הקשר בין שדות חשמליים ומגנטיים כאשר הם אינם קבועים.
שדות מגנטיים במקרים פשוטים[עריכת קוד מקור | עריכה]
שדה שנוצר על ידי תיל אינסופי[עריכת קוד מקור | עריכה]
השדה המגנטי הנוצר על ידי תיל ישר אינסופי שזורם בו זרם חשמלי ניתן על ידי חוק אמפר, שהוא גרסה אחרת של חוק ביו-סבר. חוק אמפר בצורתו האינטגרלית אומר ש־, כאשר מציין מסלול כלשהו (הנקרא "מסלול אמפר"), ו- הוא סך הזרמים החוצים את השטח המגודר על ידי מסלול זה. אנחנו כבר יודעים מהסעיף הקודם שהשדה המגנטי שנוצר על ידי זרם שהולך בקו ישר הוא במעגלים סביב כיוון הזרם, ולכן אנחנו מקבלים את הנוסחה הבאה לשדה מגנטי הנוצר על ידי תיל במרחק r מהתיל: .
שדה מגנטי הנוצר בין שני תיילים מקבילים נושאי זרם[עריכת קוד מקור | עריכה]
כאשר יש שני תיילים הנושאים זרם, נוצר ביניהם שדה מגנטי, וכתוצאה מכך מופעלים על התיילים כוחות בהתאם לכיוון השדה. כאשר שני תיילים מקבילים נושאים זרם באותו הכיוון נוצר בין שני התיילים כח משיכה. נניח שהתיילים נושאים זרם לכיוון "מעלה". נסתכל על התייל השמאלי. הוא יוצר מימינו (איפה שנמצא התייל השני) שדה מגנטי פנימה, כלומר אם נדמיין את שני התיילים על שולחן הוא יוצר שדה בכיוון מטה, כלומר בכיוון מהשולחן לרצפה (שדה בכיוון x). התייל השני נמצא כעת בתוך שדה מגנטי שכיוונו x, ולכן לפי חוקי הפיזיקה ("כלל יד ימין") הוא ימשך שמאלה, כלומר לכיוון התייל הראשון. ניתן להוכח באותה צורה שהתיל השמאלי נמשך אל הימני, או לחלופין להסיק זאת מהחוק השלישי של ניוטון. כאשר שני התיילים נושאים זרם בכיוונים מנוגדים, נוצר בין התיילים כח דחייה.
שדה מגנטי בתוך סליל[עריכת קוד מקור | עריכה]
ניתן לראות, שבתוך סליל ישנה צפיפות גבוהה של קווי שדה מגנטי, בניגוד למרחב שמחוץ לסליל. ניתן לראות גם, שהשדה המגנטי בתוך הסליל הוא בעיקרו בקו ישר ומציית לכלל יד ימין בצורה הפוכה: הפעם, האגודל מציינת את כיוון השדה המגנטי הנוצר בסליל, וכף היד - את כיוון הזרם היוצר אותו. גודל השדה, שניתן לחשבו אם משתמשים בחוק אמפר ומניחים שהשדה מחוץ לסליל הוא 0, הוא , כאשר N הוא מספר הליפופים בסליל, L הוא אורך הסליל ו-I הוא הזרם הזורם בסליל.
השדה המגנטי של כדור הארץ[עריכת קוד מקור | עריכה]
 ערך מורחב – השדה המגנטי של כדור הארץ
ערך מורחב – השדה המגנטי של כדור הארץ
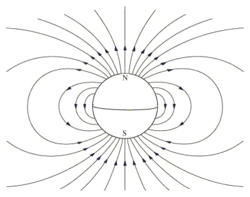
קווי השדה המגנטי של כדור הארץ מסודרים בקירוב לכיוון צפון. חומר מגנטי על פני כדור הארץ נוטה להסתדר לפי קווים אלו. ניתן לראות בכדור הארץ מגנט עצום, שקטביו בקוטב הצפוני ובקוטב הדרומי. לשדה המגנטי של כדור הארץ חשיבות רבה מבחינת קיום החיים על פניו בכך שהשדה הודף ומסיט חלקיקי קרינה המגיעים מהשמש והמסוכנים ליצורים חיים. הקטבים המגנטיים של כדור הארץ סוטים מעט מהקטבים הנוצרים כתוצאה מציר הסיבוב של כדור הארץ. לכן, ניתן למצוא במפות מדויקות קו הצפנה ל"צפון המגנטי" וקו הצפנה מעט שונה ל"צפון האמיתי". מציאת הצפון המגנטי נעשית באמצעות מצפן, מכשיר ובו מחט הנעה על ציר ומתיישרת לאורך הרכיב המשיקי של קו השדה המגנטי של כדור הארץ בנקודה הנמדדת. מחט המצפן היא דיפול מגנטי קטן בפני עצמה, וצדה הפונה צפונה הוא צד ה"דרום" בדיפול זה.
ראו גם[עריכת קוד מקור | עריכה]
- מגנטיות ומגנט
- שטף מגנטי
- השדה המגנטי של כדור הארץ
- דיפול
- אלקטרומגנט
- אלקטרומגנטיות
- משוואות מקסוול
- טנזור השדה האלקטרומגנטי
- מכשיר MRI
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- ארז גרטי, מהם קווי שדה מגנטי?, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 2 ביולי 2011
- הכוח המגנטי בין שני מטענים בתנועה יחסית
- שדה מגנטי, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ G. Jezek (2006), History Of Magnets
- ^ R. T. Merrill, M. W. McElhinny (1983), The earth's magnetic field: its history, origin, and planetary perspective






































