אלסטיות
|
עיינו גם בפורטל פורטל הפיזיקה מהווה שער לחובבי הפיזיקה ולמתעניינים בתחום. בין היתר, בפורטל תוכלו למצוא מידע על פיזיקאים חשובים, על ענפי הפיזיקה ועל תאוריות פיזיקליות. |
אלסטיות[1] או גמישות היא תכונתו של חומר המתארת את התנגדותו למַעֲוָת (דפורמציה) חיצוני, ואת יכולתו של החומר לחזור לצורתו ולממדיו המקוריים לאחר הסרת הכוח המעוות. זוהי תורה מקרוסקופית, כלומר היא אינה מתחשבת במרכיביו המיקרוסקופיים של החומר. חקר האלסטיות מנסה ליצור מודל מתמטי המכמת את תגובת החומר למעוות המופעל עליו, במקרים בהם מתאפשרת הזנחת התהליכים המיקרוסקופיים המרכיבים את החומר.
מבוא איכותני
[עריכת קוד מקור | עריכה]על מנת לתאר את האלסטיות של החומר מבחינה פיזיקלית הוגדרו שני פרמטרים הראשון נקרא 'סבילות לעיוות' או מודולוס, אשר מוגדר על ידי כמות הכוח שצריך להפעיל ליחידת שטח על מנת לגרום לעיוות, כלומר כמה קשה לעוות את החומר. הפרמטר השני הוא גבול המתיחה, אשר מוגדר כמתיחה המקסימלית שחומר יכול להכיל לפני שנגרם לו עיוות קבוע, כלומר כמה החומר מסוגל להימתח בלי להשתנות. יחידותיהם של שני הפרמטרים הן פסקל (pa).
שני הפרמטרים הם בלתי תלויים זה בזה, ויכולים להיות חומרים אשר הם בעלי מודולוס גבוה וגבול מתיחה נמוך כמו מתכות, או בעלי גבול מתיחה גבוה ומודולוס נמוך כמו גומיות. לרוב בשימוש היומיומי המונח אלסטיות משמש רק לגבול המתיחה.
היווצרות גבול המתיחה
[עריכת קוד מקור | עריכה]כאשר מפעילים כוח על גוף נוצרת הזזה של חלקיו. ניתן לחלק את ההשפעה על הגוף לשני חלקים:
- הזזה של גוף קשיח – הזזה שבה המרחקים בין החלקיקים המרכיבים את הגוף עליו מופעל הכוח לא משתנים, כלומר הזזה של הגוף במלואו כמכלול.
- מַעֲוַת או דפורמציה[2] – הזזה שבה המרחק היחסי בין חלקיקים כן משתנה ובהתאם לכך משתנה צורתו וגודלו.
כאשר נוצרת אנרגיה פוטנציאלית כתוצאה מהפעלת כוח על גוף, כל עוד אינם מחסומים אנרגטיים ייטה הגוף להגיע למצב בו האנרגיה הפוטנציאלית הכי נמוכה. במקרים מסוימים נטייה זו יכולה לגרום לגוף לחזור למצבו המקורי. דוגמה לדבר היא העלאת כדור במעלה הר. על הכדור מושקע כוח נגד כיוון משיכת כדור הארץ המעניק לכדור אנרגיה פוטנציאלית כובדית. בהסרת הכוח המעלה את הכדור יידרדר הכדור במורד המדרון ובכך יחזור למקומו. תופעה זו מתרחשת הן בהעתקה ליניארית והן במקרה של דפורמציה ובשני המקרים מקור האנרגיה הפוטנציאלית משתנה בין סביבות שונות עליהן פועל הכוח. במתכות האנרגיה הפוטנציאלית נוצרת כיוון שסידור האטומים בסריג המתכתי הוא בעל אנרגיה פוטנציאלית נמוכה יחסית למצב לא מסודר. כאשר מופעל כוח על השריג המתכתי ונשברת צורת השריג נוצרת אנרגיה פוטנציאלית כיוון שמולקולות המתכת ייטו להסתדר מחדש בצורת השריג המקורי. אי לכך כאשר יוסר הכוח האטומים המרכיבים את השריג כל עוד הכוח המופעל ליחידת שטח לא עבר רף מסוים המשנה את שריג שיווי המשקל המולקולות ייטו לחזור למצב היציב ולכן יסתדרו מחדש בצורת שריג שקרוב יותר למצב ההתחלתי בו היה שרוי החומר מאשר המצב אחר הפעלת הכוח, הרף המשנה את השריג בו יימצא שיווי המשקל באופן לא זניח מוגדר כגבול המתיחה.
חומר אלסטי מושלם
[עריכת קוד מקור | עריכה]כאשר גבול המתיחה שואף לאינסוף ניתן להגיד על חומר כי הוא חומר אלסטי מושלם, לחומר שכזה כל הפעלת כוח, ללא תלות בעוצמת הכוח או בסוגו, לא תשנה את צורתו או את נפחו, חומר כזה הוא אידאה פיזיקלית אך כיום במדע החומרים ובפיזיקה של מצב מוצק מתקיימים מחקרים רבים השואפים לפתח חומרים המתקרבים כמה שיותר לחומר אלסטי מושלם כיוון שככל שחומר יותר אלסטי פחות תתבזבז אנרגיה עקב לחצים חיצוניים על המערכת.
תנועות אלסטודינמיות
[עריכת קוד מקור | עריכה]
לעיתים הפעלת כוח על גוף תגרום להחלפה מתמדת בין אנרגיות פוטנציאליות, מה שיגרום לתנודות מחזוריות כיוון שאין נקודת שיווי משקל בה האנרגיה הפוטנציאלי מינימלית. תופעה זו נפוצה בטבע וניתן לראות אותה בין היתר בקפיצים, במיתרים רוטטים וברעידות אדמה. כתוצאה מהתנודות ניתן לכמת את תדר התנועה ואורך הגל שלה, והיא הבסיס לגלים מכניים. בפועל כתוצאה ישירה מהחוק השני של התרמודינמיקה המערכת בסופו של דבר תפסיק לנוע באופן הניתן למדידה בטכניקות מאקרוסקופיות, כיוון שאנרגיית המערכת תתפזר לחום. ניתוח של חומרים אלסטיים אידיאליים נלמד כבר במסגרות תיכוניות והוא זכה לכינוי תנועות הרמוניות.
ניתוח מתמטי
[עריכת קוד מקור | עריכה]המודל הפשטני ביותר המציע ניתוח של אלסטיות החומר הוא מודל אשר הוצע על ידי החוקר רוברט הוק על סמך תצפיות אמפיריות על חומרים. הוק מצא כי חומרים ספציפיים תחת לחצים בקנה מידה קטן מתארכים בעקבות מתיחה באופן הפרופורציונלי לכוח המותח. בעקבות כך הוא פיתח מערכת מכנית פשוטה למדידת קבוע הפרופורציה לחומרים שונים, קבוע זה מייצג בקירוב גס את מידת המודולוס של החומר הנמתח המאפיין חלק מהאלסטיות החומר. לאחר התפתחות המדע והכלים המתמטים וההנדסיים בהם המדע משתמש נוצרו שיטות מתמטיות מורכבות המשתמשות בתורת הטנזורים ואנליזה וקטורית מתקדמת על מנת לכמת את כמות המעוות גם לחומרים היוצאים מגדר ההגבלות של הוק ואף של נוזלים לא ניוטונים המציגים תכונות אלסטיות תחת לחצים גבוהים ומהירים. באופן מעשי משתמשים בהנדסה בשיטות קירובים נומריות ואת החישובים עושים אלגוריתמים ממחשבים.
חוק הוק
[עריכת קוד מקור | עריכה]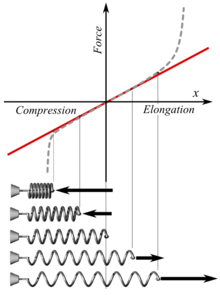
אנליזה מודרנית
[עריכת קוד מקור | עריכה]ניתוח מדויק לכלל החומרים ולכלל הכוחות המופעלים על גוף התפתח במאות האחרונות, והיכולת להשתמש במחשבים על מנת לבצע סימולציות תרמה רבות לעדכון השיטות. להלן יוצגו המשוואות המתמטיות העומדות בבסיס האנליזה.
אלסטיות לא ליניארית
[עריכת קוד מקור | עריכה]אלסטיות לא ליניארית מתארת תהליך הפיך בו מבצעים דפורמציה לחומר ללא הנחה שהדפורמציה קטנה. מצב ההתחלה, לפני הדפורמציה, נקרא מצב הייחוס. נוח לתאר את המצב לפני ואחרי הדפורמציה באמצעות הווקטורים:
| לפני הדפורמציה | אחרי הדפורמציה |
התורה האלסטית מניחה שהאנרגיה הדרושה לביצוע דפורמציה תלויה רק בשינוי המרחק בין חלקיקי החומר. כלומר ניתן לרשום:
כאשר מוגדרת להיות המטריקה.
אלסטיות ליניארית[3]
[עריכת קוד מקור | עריכה]כאשר קטן יחסית ל- ניתן לקרב ליניארית את הנגזרות של s ולהזניח סדרים גבוהים מסדר ראשון. סך הכל מתקבל:

וכדי לקבל את התאוריה לאלסטיות, ניתן להניח שהאנרגיה החופשית לביצוע דפורמציה הולכת כמו ריבוע טנזור המעוות, וזה כדי שכאשר האנרגיה תהיה במינימום (מה שלא מתקבל באיבר ליניארי) – לא מבצעים דפורמציה. אם כך, נכתוב את האנרגיה החופשית (תוך הנחת לוקאליות של הבעיה):
כאשר אינדקסים חוזרים נסכמים.
בלי הגבלת הכלליות ניתן לבחור את C כך שהוא יהיה סימטרי בהחלפה של כך שסה״כ נשאר עם 21 מקדמים בלתי תלויים. תחת סימטריות ניתן להוריד את מספר הקבועים הללו, לדוגמה בסימטריה קובית נישאר עם 3 מקדמים בת״ל בלבד.
נהוג לסמן את טנזור הלחץ:
ואז לקבל:
אלסטיות בסימטריה קובית
[עריכת קוד מקור | עריכה]סימטריה קובית מוגדרת ככזאת שקיימות בה סימטריות תחת שיקופים בכל אחד מהצירים. ניתן להראות שבמקרה זה נשארים עם שלושה קבועים בלבד מתוך כל ה-21: ו-.
נקבל את הביטוי לאנרגיה חופשית[4]:
נהוג במקרה זה לסמן:
;
ובאותו אופן מגדירים את הגדלים . נקבל:
עתה ניתן מתוך האנרגיה החופשית לחשב את מודול הנפח על ידי:
ובמקרה של שריג קובי בו מופעל לחץ אחיד על כל הדפנות מתקבל:
אלסטיות בסימטריה איזוטרופית
[עריכת קוד מקור | עריכה]בגוף בו קיימת סימטריה איזוטרופית, נוספת סימטריה נוספת לבעיית הסימטריה הקובית – סימטריית סיבוב. כלומר אם לכתוב:
כאשר R היא מטריצת סיבוב כלשהי. נרצה שתחת סיבוב כזה האנרגיה החופשית לא תשתנה.
ניתן על ידי בחירת מטריצת סיבוב המתאימה ל-45 מעלות ודרישה לשוויון באנרגיה החופשית בין המצב ההתחלתי למצב המסובב להראות שמשלושה קבועים בלתי תלויים, יורדים לשני קבועים בלבד. כאשר הקבוע השלישי ניתן על ידי:
במקרה זה נוכל לכתוב[5]:
כאשר:
נקראים קבועי לאמה.
ניתן לקבל אינטואיציה למשמעותם של הגדלים המופיעים בביטוי באנרגיה החופשית על ידי כתיבת משוואות התנועה של הגוף. נוסיף איבר קינטי סטנדרטי מהצורה:

כאשר צפיפות המסה.
באמצעות משוואות אוילר-לגראנז' מתקבלת משוואת התנועה:
על ידי אינטגרציה בשני הצדדים ניתן לראות את הדבר הבא:
צד שמאל מהווה על פי הגדרה את הכוח המופעל על הגוף. בצד ימין ניתן להפעיל את משפט גאוס ולקבל שהכוח הפועל על גוף ניתן על ידי החלק המתאים בטנור הלחץ. ומכאן שמו, שכן הוא באמת מתאר את הלחץ המופעל על גוף בכל אחת מפאותיו. נשים לב שכצפוי הכוח מגיע משפות הגוף בלבד. ניתן לראות באיור את חלקיו של הטנזור.
במקרה האיזוטרופי נוכל לכתוב:
ועל ידי הפיכת המטריצה מתקבל:
אם נפעיל על הגוף לחץ אחיד S בכיוון z נוכל לחשב את מודול יאנג:
גביש נוזלי
[עריכת קוד מקור | עריכה]גביש נוזלי[6] היא פאזה בחומר בין מוצק לנוזל בה קיים כיוון מועדף למולקולות. כיוון זה נקרא ה-director ונסמן אותו ב-. תורה אלסטית לגביש נוזלי חשובה לדוגמה להבנת כמות האנרגיה הדרושה לשינוי כיוון המולקולות. דבר הכרחי לדוגמה בבניית מסכי LCD. תורה[7] כזו מניחה שהאנרגיה הדרושה לשינוי כיוון ה-director תלויה רק בנגזרות שונות של n תחת ההנחות:
- חייבת להיות סימטריה תחת שיקוף – קרי מעבר בין ל-.
- אין תלות בבחירת מערכת הצירים – חייבת להיות סימטריה לסיבוב והזזה של הראשית.
ניתן להראות שתחת הנחות אלו נגזרות ראשונות מתבטלות. נשאר לחפש איברים מסדר שני.
לאחר הרבה אלגברה ושימוש בהנחות אלו מקבלים לבסוף שהאנרגיה החופשית ניתנת על ידי
ראו גם
[עריכת קוד מקור | עריכה]לקריאה נוספת
[עריכת קוד מקור | עריכה]- M.P Marder, Condensed Matter Physics, Wiley & Sons
- L.D. Landau, E.M. Lifshitz, Course of Theoretical Physics: Theory of Elasticity Butterworth-Heinemann.
- J.E. Marsden, T.J. Hughes, Mathematical Foundations of Elasticity, Dover.
- P.C. Chou, N. J. Pagano, Elasticity: Tensor, Dyadic, and Engineering Approaches, Dover.
- R.W. Ogden, Non-linear Elastic Deformation, Dover.
- Sybil P. Parker Editor in Chieh. McGraw-Hill Encyclopedia of Engineering, McGraw Hill Book Company.
- S.P. Timoshenkoo & J.N. Goodier Theory of Elasticity, 3rd edition, International Student Edition, McGraw -Hill 1970.
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- אלסטיות, איך דברים מתעוותים (באנגלית)
- אלסטיות במילון מרים וובסטר (באנגלית)
- אלסטיות באתר answers.com (באנגלית)
- אלסטיות, באתר אנציקלופדיה בריטניקה (באנגלית)
 אלסטיות, דף שער בספרייה הלאומית
אלסטיות, דף שער בספרייה הלאומית
הערות שוליים
[עריכת קוד מקור | עריכה]- ^ F. D. MURNAGHAN., FINITE DEFORMATIONS OF AN ELASTIC SOLID.*, American Journal of Mathematics
- ^ A. E. H. Love, The Small Free Vibrations and Deformation of a Thin Elastic Shell, The Royal Society
- ^ B.R. Seth, Finite Strain in Elastic Problems, The Royal Society Publishing
- ^ FRANCIS BIRCH, Finite Elastic Strain of Cubic Crystals, PHYSICAL REVIEW
- ^ M. Mooney, A theory of large elastic deformation, Journal of Applied Physics
- ^ Michael J.Stephen and Joseph P. Straley, Physics of liquid crystals, REVIEWS OF MODERN PHYSICS
- ^ F. C. FRA, ON THE THEORY OF LIQUID CRYSTALS, Discussions of the Faraday Society
| מכניקת הרצף תחום בפיזיקה העוסק בחומרים רציפים. |
מכניקת מוצקים תחום בפיזיקה העוסק בחומרים רציפים הנמצאים במצב מנוחה. |
אלסטיות מתאר חומרים החוזרים למצב המנוחה, לאחר הסרת המאמצים (לחצים). | |
| פלסטיות מתאר חומרים המתעוותים לצמיתות לאחר הפעלת רף מסוים של מאמץ. |
ראולוגיה תחום העוסק בחומרים בעלי מאפיינים מוצקים וזורמים. | ||
| מכניקת זורמים התחום בפיזיקה העוסק בחומרים רציפים המתעוותים בחשיפה לכוח. |
זורמים לא-ניוטונים חווים את שיעורי המעוות באופן שאינו פרופורציוני למאמץ הגזירה המופעל עליהם. | ||
| זורמים ניוטונים חווים את שיעורי המעוות באופן פרופורציוני למאמץ הגזירה המופעל עליהם. | |||
| מאמץ (הנדסה) | ||
|---|---|---|
| מאמצים | מאמץ • מאמץ גזירה • מאמץ כפיפה • מאמץ לחיצה • מאמץ מתיחה • מאמץ פיתול • מאמץ קריסה • עייפות החומר | |
| נושאי עזר | מומנט כפיפה • מומנט כוח • אלסטיות • מעוות • חוק הוק • עקומת מאמץ-מעוות • כניעה (הנדסה) | |
| מודולי האלסטיות | מודול האלסטיות • מודול הגזירה • מקדם פואסון • קבועי לאמה • מודול הנפח | |
| שטחים ונפחים | שטח • מומנט התמד • מומנט ההתמד של השטח • מומנט התמד פולרי של השטח • משפט שטיינר-הויגנס • טנזור התמד • טבלת טנזורי התמד • מומנט ראשון של שטח | |
| נושאים משלימים | חוזק חומרים • טנזור מאמצים • מאמצים ראשיים • מעגל מור • היפותזות חוזק • שיטות אנרגיה • חוקי קסטיליאנו | |























![{\displaystyle \Rightarrow F=\int dr\left[{\frac {1}{6}}\left(C_{11}+2C_{12}\right)\left({\frac {\delta V}{V}}\right)^{2}\right]\Rightarrow B={\frac {1}{3}}\left(C_{11}+2C_{12}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1513762add35d6e71f23c12b7810b60d3c7b5ff7)












