התרחבות זמן כבידתית
יש לשכתב ערך זה. הסיבה היא: ניסוח, תרגמת.
| ||
| יש לשכתב ערך זה. הסיבה היא: ניסוח, תרגמת. | |
התרחבות זמן כבידתית היא סוג של התרחבות זמן, הפרש הזמן שחלף בין שני אירועים כפי שנמדד על ידי צופים שנמצאים במרחקים שונים ממסת הכבידה. ככל שהאנרגיה הפוטנציאלית נמוכה יותר (ככל שהשעון קרוב יותר למקור הכבידה), כך הזמן חולף לאט יותר, ככל שהאנרגיה הפוטנציאלית עולה (השעון מתרחק ממקור הכבידה) הפרש הזמנים הנמדד יהיה קטן יותר. אלברט איינשטיין חזה במקור את האפקט הזה בתורת היחסות שלו וזה אושר מאז על ידי מבחני תורת היחסות הכללית.[1]
האפקט מודגם במצב בו שעונים אטומיים בגבהים שונים (וכך אנרגיה פוטנציאלית שונה) מראים בסופו של דבר זמנים שונים. ההשפעות שהתגלו בניסויים הקשורים לכדור הארץ הן קטנות ביותר, כאשר נמדדים הבדלים בננו שניות. יחסית לגיל כדור הארץ במיליארדי שנים, ליבתו של כדור הארץ צעירה למעשה ב -2.5 שנים מעל פני השטח שלה.[2] קבלת השפעות גדולות יותר תדרוש מרחקים גדולים יותר מכדור הארץ או ממקור כבידה גדול יותר.
התרחבות זמן כבידתית תוארה לראשונה על ידי אלברט איינשטיין בשנת 1907[3] כתוצאה של תורת היחסות הפרטית כאשר מדברים על מערכות ייחוס מואצות. בתורת היחסות הכללית, התרחבות הזמן נחשבת כהפרשים במדידת הזמן העצמי במיקומים שונים כמתואר על ידי טנסור מטרי של המרחב-זמן. קיומו של התרחבות זמן הכבידה אושר לראשונה ישירות על ידי ניסוי פאונד-רבקה בשנת 1959.
הַגדָרָה[עריכת קוד מקור | עריכה]
שעונים המרוחקים מגופים מאסיביים (או בעלי אנרגיה פוטנציאלית כבידתית גבוהה יותר) פועלים מהר יותר, ושעונים הקרובים לגופים מאסיביים (או בעלי אנרגיה פוטנציאלית כבידתית נמוכה יותר) פועלים לאט יותר. לדוגמה, אם נתחשב בפרק הזמן הכולל של כדור הארץ (4.6 מיליארד שנים), שעון שנמצא במצב גיאוסטציונרי בגובה של 9,000 מטר מעל פני הים, כמו אולי בראש הר האוורסט (8,848 מטר), יקדים בערך ב-39 שעות את השעון שהוצב בגובה פני הים.[4][5] זאת כיוון שהתרחבות זמן כבידתית באה לידי ביטוי במסגרות ייחוס מואצות, או מתוקף עקרון השוויון בשדה כבידה של עצמים מאסיביים.[6]
לפי תורת היחסות הכללית, המסה האינרציאלית והמסה הכבידתית זהות זו לזו, וכל מערכות הייחוס המואצות (כמו מערכת ייחוס המסתובבת באופן אחיד עם התרחבות הזמן העצמי שלה) שקולות פיזית לשדה הכבידה באותו חוזק.[7]
אם ניקח קבוצת משקיפים לאורך קו "אנכי" ישר, שכל אחד מהם חווה כוח g קבוע שכיוונו לאורך קו זה (למשל חללית ארוכה שמאיצה,[8][9] גורד שחקים, פיר בכוכב לכת). כאשר יבטא את התלות של כוח ה-g ב"גובה", וניקח קואורדינטה לאורך הקו המוזכר. המשוואה ביחס לצופה ב- היא
כאשר הוא התרחבות הזמן הכוללת במצב מרוחק , היא התלות של כוח ה-g בגובה , היא מהירות האור, ו- היא הפונקציה המעריכית בבסיס e.
לשם הפשטות, בתיאור לפי קואורדינטות של רינדלר (אנ') במרחב-זמן שטוח, התלות תהיה:
עם הקבוע , שמניב
- .
מצד שני, כאשר הוא כמעט קבוע ו- הוא הרבה יותר קטן מ , ניתן להשתמש בקירוב הליניארי, המכונה "שדה חלש": .
מחוץ לכדור שאינו מסתובב[עריכת קוד מקור | עריכה]
משוואה נפוצה המשמשת לקביעת התרחבות זמן כבידתית נגזרת ממטריקת שוורצשילד, המתארת את המרחב-זמן בסביבתו של עצם כדורי סימטרי מסיבי שאינו מסתובב. המשוואה היא:
כאשר
- הוא הזמן העצמי בין שני אירועים עבור צופה הקרוב לכדור המסיבי, כלומר עמוק בתוך שדה הכבידה
- הוא זמן הקואורדינטות בין האירועים עבור צופה במרחק גדול באופן שרירותי מהאובייקט המסיבי (בהנחה שהצופה הרחוק משתמש בקואורדינטות של שוורצשילד, מערכת קואורדינטות שבה שעון במרחק אינסופי מהסביבה המסיבית היה מתקתק בשנייה אחת לשנייה של זמן הקואורדינטות, בעוד שעונים קרובים יותר היו מתקתקים בקצב מופחת מזה),
- הוא קבוע הכבידה ,
- היא מסת העצם היוצר את שדה הכבידה,
- הוא הקואורדינטה הרדיאלית של הצופה בשדה הכבידה (קואורדינטה זו מקבילה למרחק הקלאסי ממרכז האובייקט, אך היא למעשה קואורדינטת שוורצשילד; למשוואה בצורה זו יש פתרונות אמיתיים ל ),
- הוא מהירות האור ,
- הוא רדיוס שוורצשילד של ,
- הוא מהירות הבריחה, ו
- היא מהירות הבריחה, הבאה לידי ביטוי כשבריר ממהירות האור c.
כדי להמחיש זאת, מבלי להסביר את השפעות הסיבוב של הכדור, הקרבה למקור הכבידה של כדור הארץ תגרום לשעון על פני כדור הארץ להראות 0.0219 פחות שניות לאורך תקופה של שנה מאשר שעון של צופה מרוחק. לשם השוואה, שעון על פני השמש יראה כ-66.4 פחות שניות בשנה אחת.
מסלול מעגלי[עריכת קוד מקור | עריכה]
במטריקת שוורצשילד, חפצים הנופלים נפילה חופשית יכולים להגיע למסלול מעגלי אם רדיוס המסלול שלהם גדול מ- (רדיוס כדור הפוטון). הנוסחה של שעון במנוחה ניתנת למעלה; הנוסחה שלהלן נותנת את התרחבות הזמן הכבידתית מעל מסלול אחד לשעון במסלול מעגלי: [10][11]
שתי ההרחבות מוצגות באיור שלהלן.
מאפיינים חשובים של התרחבות זמן הכבידה[עריכת קוד מקור | עריכה]
- על פי תאוריית היחסות הכללית, התרחבות זמן כבידתית תואמת את קיומה של מערכות ייחוס מואצת. בנוסף, כל התופעות הפיזיקליות בנסיבות דומות עוברות התרחבות זמן באופן שווה על פי עקרון השוויון הנהוג בתורת היחסות הכללית .
- מהירות האור בסביבה היא תמיד שווה ל- c לפי הצופה שנמצא שם. כלומר, לכל אזור אינפיניטסימלי במרחב-זמן ניתן להקצות זמן עצמי משלו ומהירות האור בהתאם לזמן הנכון באותו אזור היא תמיד c . זה המקרה בין אם אזור נתפס על ידי צופה או לא. ניתן למדוד עיכוב זמן עבור פוטונים הנפלטים מכדור הארץ, מתעקמים ליד השמש, נוסעים לוונוס ואז חוזרים לכדור הארץ בדרך דומה. אין כאן הפרה של קביעות מהירות האור כאן, שכן כל מתבונן המתבונן במהירות הפוטונים באזורם ימצא את המהירות של אותם פוטונים להיות c, ואילו המהירות בה אנו צופים באור הנע מרחקים סופיים בסביבה של השמש יהיה שונה מ- c .
- אם מתבונן מסוגל לעקוב אחר האור באזור מרוחק ואחר עוד צופה ליד גוף מסיבי, הצופה הראשון רואה כי גם האור המרוחק וגם לצופה שזמנו מורחב יש שעון איטי יותר מאשר אור אחר שמגיע לצופה הראשון במהירות c, כמו כל אור אחר המתבונן הראשון באמת יכול לצפות (במיקום שלהם). אם האור המרוחק האחר מגיע בסופו של דבר אל הצופה הראשון, גם הוא יימדד על ידי הצופה הראשון ב- c .
- התרחבות זמן כבידתית במקור כבידה שווה להתרחבות זמן במהירות למהירות הנדרשת כדי לברוח מאותו שדה כבידה (בהתחשב בעובדה שהמטריקה היא של הצורה כלומר, זהו זמן בלתי סדיר ואין מונחים "תנועתיים" ). כדי להראות זאת, ניתן להחיל את משפט נתר (פיזיקה) על גוף שנופל בחופשיות למקור הכבידה מאין סוף. לאחר מכן, השינוי בזמן של המטריקה מרמז על שמירת הכמות , כאשר הוא מרכיב הזמן של ה-4-מהירות של הגוף. באינסוף , כך , או בקואורדינטות המותאמות להרחבת הזמן המקומית, ; כלומר, התרחבות זמן בגלל המהירות שנרכשה (כפי שנמדדת במיקום הגוף הנופל) שווה להרחבת זמן הכבידה בבאר שהגוף נפל לתוכה. באופן כללי יותר על שימוש בטענה זו, ניתן לקבל כי (תחת אותן הנחות על הערך) התרחבות הזמן הכבידתית היחסית בין שתי נקודות שווה להתרחבות הזמן הנגרמת מהמהירות הדרושה כדי לטפס מהנקודה התחתונה לגבוהה.
אישור בניסוי[עריכת קוד מקור | עריכה]
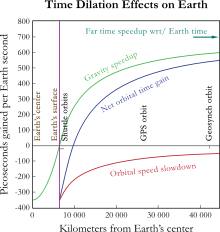
התרחבות הזמן הכבידתית נמדדה בניסוי באמצעות שעונים אטומיים במטוסים. השעונים על סיפון המטוסים היו מעט מהירים יותר מאשר שעונים על הקרקע. ההשפעה הייתה מספיק משמעותית כדי שהלוויינים המלאכותיים של מערכת המיקום הגלובלי יצטרכו לתקן את שעוניהם.[12]
בנוסף, בדיקות של התרחבות הזמן בשל הפרשי גובה של פחות ממטר אחד אושרו במעבדה.[13]
התרחבות הזמן הכבידתית אושרה גם על ידי ניסוי פאונד-רבקה, תצפיות על הספקטרום של הננס הלבן סיריוס B, וניסויים עם אותות זמן שנשלחו אל נחת מאדים ויקינג 1 וממנה.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Grøn, Øyvind; Næss, Arne (2011). Einstein's Theory: A Rigorous Introduction for the Mathematically Untrained. Springer. ISBN 9781461407058.
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Einstein, A. (בפברואר 2004). Relativity : the Special and General Theory by Albert Einstein. Project Gutenberg.
{{cite book}}: (עזרה) - ^ Uggerhøj, U I; Mikkelsen, R E; Faye, J (2016). "The young centre of the Earth". European Journal of Physics. 37 (3): 035602. arXiv:1604.05507. Bibcode:2016EJPh...37c5602U. doi:10.1088/0143-0807/37/3/035602.
- ^ A. Einstein, "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen", Jahrbuch der Radioaktivität und Elektronik 4, 411–462 (1907); English translation, in "On the relativity principle and the conclusions drawn from it", in "The Collected Papers", v.2, 433–484 (1989); also in H M Schwartz, "Einstein's comprehensive 1907 essay on relativity, part I", American Journal of Physics vol.45,no.6 (1977) pp.512–517; Part II in American Journal of Physics vol.45 no.9 (1977), pp.811–817; Part III in American Journal of Physics vol.45 no.10 (1977), pp.899–902, see parts I, II and III.
- ^ Hassani, Sadri (2011). From Atoms to Galaxies: A Conceptual Physics Approach to Scientific Awareness. CRC Press. p. 433. ISBN 978-1-4398-0850-4. Extract of page 433
- ^ Topper, David (2012). How Einstein Created Relativity out of Physics and Astronomy (illustrated ed.). Springer Science & Business Media. p. 118. ISBN 978-1-4614-4781-8. Extract of page 118
- ^ John A. Auping, Proceedings of the International Conference on Two Cosmological Models, Plaza y Valdes, ISBN 9786074025309
- ^ Johan F Prins, On Einstein's Non-Simultaneity, Length-Contraction and Time-Dilation
- ^ Kogut, John B. (2012). Introduction to Relativity: For Physicists and Astronomers (illustrated ed.). Academic Press. p. 112. ISBN 978-0-08-092408-3.
- ^ Bennett, Jeffrey (2014). What Is Relativity?: An Intuitive Introduction to Einstein's Ideas, and Why They Matter (illustrated ed.). Columbia University Press. p. 120. ISBN 978-0-231-53703-2. Extract of page 120
- ^ Keeton, Keeton (2014). Principles of Astrophysics: Using Gravity and Stellar Physics to Explore the Cosmos (illustrated ed.). Springer. p. 208. ISBN 978-1-4614-9236-8. Extract of page 208
- ^ Taylor, Edwin F.; Wheeler, John Archibald (2000). Exploring Black Holes. Addison Wesley Longman. p. 8-22. ISBN 978-0-201-38423-9.
- ^ Richard Wolfson (2003). Simply Einstein. W W Norton & Co. p. 216. ISBN 978-0-393-05154-4.
- ^ C. W. Chou, D. B. Hume, T. Rosenband, D. J. Wineland (24 September 2010), "Optical clocks and relativity", Science, 329(5999): 1630–1633;



![{\displaystyle T_{d}(h)=\exp \left[{\frac {1}{c^{2}}}\int _{0}^{h}g(h')dh'\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e92b810fcba5e86d459b67c9ae95d13c993b951)































