כוכב (גאומטריה)

כוכב, כמושג כללי, אינו מוגדר בגאומטריה, אך ישנם קווים שבורים סגורים שניתן לראותם כדמויי כוכב. רק כוכבים שכל צלעותיהם וזוויותיהם שוות (דמויי מצולעים משוכללים) מסוג זה נחקרו ביסודיות. הם נקראים כוכבים משוכללים.
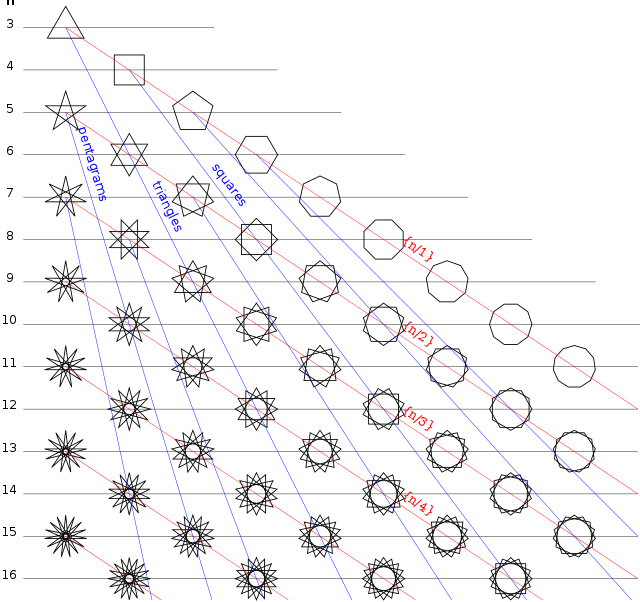
ניתן לשרטט כוכב משוכלל באמצעות חיבור אחד הקודקודים של מצולע משוכלל אל קודקוד שאינו סמוך לו (חיבור כזה קרוי אלכסון), והמשכת התהליך עד שחוזרים לקודקוד שבו התחלנו. במחומש משוכלל, למשל, ניתן ליצור פנטגרם (כוכב מחומש) באמצעות חיבור הקודקוד הראשון לקודקוד השלישי, ממנו אל הקודקוד החמישי, ממנו אל הקודקוד השני, ממנו אל הקודקוד הרביעי וממנו אל הקודקוד הראשון. תהליך זה כולל איטרציה של חיבור מודולו n, כאשר n הוא מספר הצלעות של המצולע, והמספר שאותו מוסיפים, שוב ושוב, k, גדול מ-1 וקטן מ-n-1. סימונו של כוכב כזה הוא {n/k} והוא שקול ל־{n/n-k}. פנטגרם הוא {5/2}.
שיטה דומה היא להאריך צלעות של מצולע (או פוליהדרון במרחב), עד שהמשכי הצלעות הלא-סמוכות יפגשו. שיטה זו נקראת Stellation.

כוכבים "מנוונים"
כאשר ל-n ו-k יש גורם משותף טבעי גדול מ-1, נקבל כוכב (או מצולע) בעל n/g צלעות, כאשר g הוא המחלק המשותף הגדול ביותר של n ו-k. במקרים כאלה אפשר לחזור על התהליך כאשר מתחילים בקודקוד שאינו חלק מהכוכב שקיבלנו.
דוגמאות:
- הכוכב {4/2} הוא צלב, הנוצר מ-2 פוליגונים (מנוונים בני 2 צלעות) זרים: בהנתן ריבוע בעל קודקודים 0, 1, 2, 3, אם נתחיל בקודקוד 0, סדרת המעבר על הקודקודים תהא: (0, 2, 0) (קו). אם נחזור על התהליך מקודקוד 1 נקבל את הסדרה (1, 3, 1). משתי הסדרות נקבל צלב.
- בדומה, הכוכב {6/2}: יהי משושה משוכלל בעל קודקודים 0..5. סדרות הקודקודים שנקבל הן (0, 2, 4, 0) ו-(1, 3, 5, 1). אילו שני משולשים היוצרים הקסאגרם (מגן דוד). הכוכב {6/4} הוא אותו כוכב, כאשר סדר הסדרות הוא הפוך: (0, 4, 2, 0) ו-(1, 5, 3, 1), משום ש-2 הוא המשלים ל-6 של המספר 4.
דוגמאות[עריכת קוד מקור | עריכה]
 {5/2} |
 {7/2} |
 {7/3} |
 {8/3} |
 {9/2} |
 {9/4} |
| |||||
הֵפְּטָגְרָם[עריכת קוד מקור | עריכה]
הפטגרם או ספטגרם הוא כוכב משובע שמצויר עם קווים ישרים. ישנם שני סוגים של הפטגרם:
הפטגרם חד, כוכב ה־{7/3}.

הפטגרם קהה, כוכב ה־{7/2}.

כוכבים איזוטוקסלים[עריכת קוד מקור | עריכה]
ניתן לראות כוכבים משוכללים בעלי n קודקודים כמצולע בעל 2n קודקודים, החוסם מעגל שרדיוסו r וחסום על ידי מעגל שרדיוסו R. כל קודקוד זוגי נמצא על המעגל החוסם, וכל קודקוד אי-זוגי נמצא על המעגל החסום:

תהינה 2 סדרות של נקודות E ו-I:
עבור i=0...n
נגדיר את הכוכב כקבוצת הקטעים:
אילו הם הקטעים מהנקודות הפנימיות לחיצוניות, ומהחיצוניות לפנימיות.
הבחנות[עריכת קוד מקור | עריכה]
- כוכב משוכלל כמתואר לעיל הוא מקרה פרטי של כוכב איזוטוקסלי, אשר עבורו קטעים בין קודקודים שאינם סמוכים מתלכדים עם צלעות הכוכב.
- ניתן ליצור כוכב איזוטוקסלי ממשולשים שווי שוקיים: (קטע בין נקודות Ii סמוכות, והקטעים המחברים אותן לקודקוד Ei).
- ניתן ליצור כוכב איזוטוקסלי לכל n טבעי גדול או שווה ל-2 קודקודים (כוכב בעל n=2 הוא מעוין אשר האלכסון הראשי שלו הוא קוטר המעגל החוסם, והמשני הוא קוטר המעגל החסום).
שימושים[עריכת קוד מקור | עריכה]
- צורת גלגל שיניים היא כוכב איזוטוקסלי.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
| מצולעים ופאונים | ||
|---|---|---|
| מושגים | מצולע • פאון • קודקוד • צלע • מקצוע • פאה • זווית חיצונית • אלכסון | |
| מצולעים | ||
| לפי מספר צלעות | משולש • מרובע • מחומש • משושה • משובע • מתומן | |
| משולשים | משולש ישר-זווית • משולש שווה-שוקיים • משולש שווה-צלעות | |
| מרובעים | מקבילית • טרפז • טרפז שווה-שוקיים • מרובע ציקלי • דלתון • דלתון ריצוף • מעוין • מלבן • ריבוע | |
| כוכבים | פנטגרם • מגן דוד • אניאגרם | |
| תכונות | מצולע משוכלל • מצולע שווה-צלעות • מצולע קמור • כוכב | |
| פאונים | ||
| פאונים משוכללים | ארבעון • קובייה • תמניון • תריסרון • עשרימון | |
| פאונים ארכימדיים | ארבעון קטום • קובוקטהדרון • קובייה קטומה • תמניון קטום • רומביקובוקטהדרון • קובוקטהדרון קטום • קובייה מסותתת • איקוסידודקהדרון • דודקהדרון קטום • איקוסהדרון קטום • רומביקוסידודקהדרון • איקוסידודקהדרון קטום • דודקהדרון מסותת | |
| פאונים אחרים | פירמידה • מנסרה • אנטי-מנסרה • מקבילון • מעוינון • תיבה • איקוסיטטרהדרון | |
| תכונות | פאון משוכלל • פאון משוכלל למחצה • פאון ארכימדי | |
| הכללות | ||
| הכללות | סימפלקס • היפרקובייה • טסרקט | |



