מעוין

בגאומטריה, מעוין הוא מרובע שווה צלעות. זהו מקרה פרטי של דלתון ושל מקבילית.

ריבוע הוא מקרה פרטי של מעוין.

פאון שכל פאותיו הם מעוינים נקרא מעוינון.

תכונות

תכונות המעוין הן:

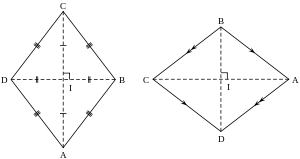
• כל הצלעות שוות באורכן (AB = BC = CD = DA)
• צלעות נגדיות מקבילות( AB || CD ; BC || DA)
• כל הגבהים שווים בארכם
• זוויות נגדיות שוות זו לזו ($\angle A = \angle C; \angle B = \angle D$)
• האלכסונים מאונכים זה לזה ($AC \perp BD$)
• האלכסונים חוצים זה את זה (AO = CO; BO = DO)
• האלכסונים חוצים את הזוויות
• היקף המעוין שווה לאורך הצלע כפול 4 ($\ P=4a$)
• בכל מעוין ניתן לחסום מעגל
• חבורת הסימטריות של מעוין שאינו ריבוע היא חבורת הארבעה של קליין.

שטח

• לפי הנוסחה לשטח של דלתון, שטח המעוין שווה למחצית מכפלת האלכסונים ($\frac{AC\cdot BD}{2}$)
• לפי הנוסחה לשטח מקבילית, שטח המעוין שווה למכפלת צלע בגובהה, וכיוון שכל הצלעות וכל הגבהים שווים במעוין, שטח המעוין שווה למכפלת הצלע בגובה ($\ a\cdot h$)
• אם אחת הזוויות של המעוין היא $\alpha$, אז השטח הוא $a^2\cdot \sin \alpha$
• אם רדיוס המעגל החסום הוא $\ r$, אז השטח הוא $\ 2a \cdot r$

קישורים חיצוניים

מיזמי קרן ויקימדיה
ספר לימוד בוויקיספר: מעויין
תמונות ומדיה בוויקישיתוף: מעוין

• מעוין, באתר MathWorld (באנגלית)