טסרקט

טֵסֵרַקְט הוא גוף במרחב ארבע-ממדי המהווה היפרקוביה מממד 4.
הטסרקט הוא הכללה של הקובייה המוכרת בגאומטריה של המרחב התלת-ממדי.
היחס בין הטסרקט לקובייה דומה לזה שבין הקובייה לריבוע. כשם שקובייה היא גוף תלת-ממדי שלו שש פאות ריבועיות, הטסרקט הוא גוף ארבע-ממדי בעל שמונה "פאות" תלת-ממדיות קובייתיות. טסרקט הוא אחד מששת הפאונים הארבע-ממדיים הקמורים המשוכללים.
את המונח "טסרקט" טבע בשנת 1888 המתמטיקאי הבריטי צ'ארלס האוורד הינטון.
תכונות הטסרקט[עריכת קוד מקור | עריכה]
לטסרקט יש 16 קודקודים, 32 מקצועות, 24 פאות דו-ממדיות, ו-8 פאות תלת-ממדיות ("תאים"). בכל קודקוד של הטסרקט נפגשים 4 מקצועות, 6 פיאות דו־ממדיות, ו-4 תאים תלת-ממדיים.
המרחק בין כל קודקוד של הטסרקט למרכז הטסרקט - נקודה שמרחקה מכל קודקודי הטסרקט שווה - הוא כאורך המקצוע של הטסרקט. המרחק בין שני קודקודים נגדיים של טסרקט הוא כפול מאורך המקצוע של הטסרקט.
בניית הטסרקט[עריכת קוד מקור | עריכה]
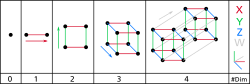
ניתן לבנות טסרקט באופן הבא, תוך הגדלה הדרגתית של מספר הממדים:
- חד-ממדי: חיבור של שתי נקודות, A ו-B בקו ישר יוצר קטע AB.
- דו-ממדי: את הקצוות של שני קטעים זהים באורכם, AB ו-CD, שהמרחק ביניהם הוא כאורך כל אחד מהם, ניתן לחבר וליצור ריבוע ABCD. לא ניתן לעשות זאת תוך שימוש בממד אחד בלבד, אלא רק במישור דו-ממדי.
- תלת-ממדי: את הקודקודים של שני ריבועים חופפים ABCD ו-EFGH, שהמרחק ביניהם הוא כאורך הצלע של כל אחד מהם, ניתן לחבר וליצור קובייה ABCDEFGH. לא ניתן לעשות זאת תוך שימוש בשני ממדים בלבד, אלא רק במרחב תלת-ממדי.
- ארבע-ממדי: את הקודקודים של שתי קוביות שאורך מקצוען זהה, ABCDEFGH ו-IJKLMNOP, והמרחק ביניהן הוא כאורך המקצוע של כל אחת מהן, ניתן לחבר וליצור טסרקט ABCDEFGHIJKLMNOP. לא ניתן לעשות זאת תוך שימוש בשלושה ממדים בלבד, אלא רק במרחב ארבע-ממדי.

-
דיאגרמת שלגל (אנ') של הטסרקט.
-
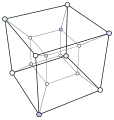
הטלה אלכסונית (אנ') (הטלה מקבילית שאינה אורתוגרפית) של הטסרקט, שמבליטה את הבנייה שלו כזוג קוביות תלת-ממדיות שקודקודיהן המתאימים מחוברים.[ב]
-
הטלה של הטסרקט אל מישור קוקסטר (אנ') של חבורת קוקסטר , שאיבריה מתאימים לסימטריות של הטסרקט. הטלה של גופים רב-ממדיים אל מישור קוקסטר של חבורות הסימטריה שלהם יוצרת הצגות מישוריות עם רמת סימטריה גבוהה.[ג]
ביאורים[עריכת קוד מקור | עריכה]
- ^ הטלה זו מטילה את הטסרקט הארבע-ממדי לתריסרון מעוייני (אנ') בתלת-ממד. לשם השוואה, בהיטל של קוביה תלת-ממדית דרך ציר שעובר באלכסון ראשי שלה, שני הקודקודים דרכם עובר הציר יוטלו אל אותה נקודה במישור, במרכזו של משושה משוכלל, ויתר קודקודי הקוביה יוטלו אל ששת קודקודי המשושה; בדומה, כאן זוג הקודקודים דרכו עובר ציר ההיטל (הקודקודים הירוקים) אמור להיות מוטל אל אותה נקודה במרחב, ויתר הקודקודים ― אל ארבעה עשר הקודקודים של התריסרון המעוייני. לטובת בהירות ההצגה והימנעות מהתלכדות קודקודים, ההטלה עוותה מעט והקודקודים המרכזיים הוזזו הצידה. הקודקודים הלבנים הם אלה שנמצאים במרחק של צלע אחת מהקודקודים הירוקים, והסגולים ― במרחק שתי צלעות. מבין הסגולים, אלה שהוטלו אל אותו גובה (במרחב התלת-ממדי) של הקודקודים הירוקים נצבעו בגוון בהיר יותר של סגול. בכל הדיאגרמות הסמוכות, אותם קודקודים בטסרקט צבועים באותם צבעים.
- ^ גם בהיטל הזה וגם בהיטל ה-vertex first, שישה עשר הקודקודים מסודרים בשורות אופקיות, וכמויות הקודקודים בכל שורה כזו שוות למספרים שבשורה 4 במשולש פסקל.
- ^ עבור הטסרקט שקודקודיו בנקודות (±1,±1,±1,±1), חבורת קוקסטר הנ"ל היא החבורה שנוצרת למשל על ידי ארבעת השיקופים x ⟷ -x, x ⟷ y, y ⟷ z, z ⟷ w. מישור קוקסטר של החבורה הזו הוא המישור (במרחב הארבע-ממדי) שתוצאת הפעלה סדרתית של כל היוצרים הנ"ל עליו תהיה סיבובו בשמינית סיבוב; 8 הוא הסדר של איבר החבורה שמתקבל מהרכבת ארבעת היוצרים. המישור אמנם תלוי בבחירת סדר הפעלת היוצרים, אך בשל הסימטריה של הטסרקט, ההיטלים על כל אחד ממישורי קוקסטר האפשריים ייתנו את אותה הדיאגרמה. עבור הסדר בו נכתבו ארבעת השיקופים לעיל (כשהראשון הוא היפוך ב-x), מישור קוקסטר הוא המישור הנפרש על ידי הוקטורים (1,√2,1,0), (0,1,√2,1).
קישורים חיצוניים[עריכת קוד מקור | עריכה]
| מצולעים ופאונים | ||
|---|---|---|
| מושגים | מצולע • פאון • קודקוד • צלע • מקצוע • פאה • זווית חיצונית • אלכסון | |
| מצולעים | ||
| לפי מספר צלעות | משולש • מרובע • מחומש • משושה • משובע • מתומן | |
| משולשים | משולש ישר-זווית • משולש שווה-שוקיים • משולש שווה-צלעות | |
| מרובעים | מקבילית • טרפז • טרפז שווה-שוקיים • מרובע ציקלי • דלתון • דלתון ריצוף • מעוין • מלבן • ריבוע | |
| כוכבים | פנטגרם • מגן דוד • אניאגרם | |
| תכונות | מצולע משוכלל • מצולע שווה-צלעות • מצולע קמור • כוכב | |
| פאונים | ||
| פאונים משוכללים | ארבעון • קובייה • תמניון • תריסרון • עשרימון | |
| פאונים ארכימדיים | ארבעון קטום • קובוקטהדרון • קובייה קטומה • תמניון קטום • רומביקובוקטהדרון • קובוקטהדרון קטום • קובייה מסותתת • איקוסידודקהדרון • דודקהדרון קטום • איקוסהדרון קטום • רומביקוסידודקהדרון • איקוסידודקהדרון קטום • דודקהדרון מסותת | |
| פאונים אחרים | פירמידה • מנסרה • אנטי-מנסרה • מקבילון • מעוינון • תיבה • איקוסיטטרהדרון | |
| תכונות | פאון משוכלל • פאון משוכלל למחצה • פאון ארכימדי | |
| הכללות | ||
| הכללות | סימפלקס • היפרקובייה • טסרקט | |

![הטלה אורתוגרפית מסוג vertex-first (אנ').[א]](http://upload.wikimedia.org/wikipedia/commons/thumb/5/59/Hypercubeorder.svg/111px-Hypercubeorder.svg.png)
![הטלה אלכסונית (אנ') (הטלה מקבילית שאינה אורתוגרפית) של הטסרקט, שמבליטה את הבנייה שלו כזוג קוביות תלת-ממדיות שקודקודיהן המתאימים מחוברים.[ב]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3f/Hypercubecubes.svg/120px-Hypercubecubes.svg.png)
![הטלה של הטסרקט אל מישור קוקסטר (אנ') של חבורת קוקסטר '"`UNIQ--postMath-00000001-QINU`"', שאיבריה מתאימים לסימטריות של הטסרקט. הטלה של גופים רב-ממדיים אל מישור קוקסטר של חבורות הסימטריה שלהם יוצרת הצגות מישוריות עם רמת סימטריה גבוהה.[ג]](http://upload.wikimedia.org/wikipedia/commons/thumb/f/f8/Hypercubestar.svg/120px-Hypercubestar.svg.png)
