קואורדינטות

מערכות צירים וקואורדינטות

מערכות צירים נפוצות

ראו גם

קוֹאוֹרְדִּינָטוֹת (בעברית: שיעורים) הן קבוצת מספרים המציינת את מיקומו של גוף במרחב כלשהו. מערכת הקואורדינטות (או מערכת הצירים) שנקבעת כדי לתאר את המרחב היא שרירותית לחלוטין, אם כי בדרך כלל יש מספר מערכות קואורדינטות טבעיות שבהן נוח במיוחד לתאר מרחבים מסוימים.

קואורדינטות גאוגרפיות

ערך מורחב – קואורדינטות גאוגרפיות

בגאוגרפיה, ובפרט בטופוגרפיה, קואורדינטה היא מיקומה המדויק של נקודה על מפה שמורכבת מקווי אורך ורוחב. יש לציין שאף על פי שקווי האורך והרוחב יוצרים רשת שהיא שתי וערב (מערכת אורתוגונלית) לא מדובר בקואורדינטות קרטזיות בגלל העקמומיות של פני כדור הארץ.

מפה של כדור הארץ המציגה את קווי האורך והרוחב המשמשים למיקום אזורים על הכדור

הנקודה (a,b) מורכבת משני חלקים:

קואורדינטה a – מייצגת את קו הרוחב שבמפה.
קואורדינטה b – מייצגת את קו האורך שבמפה.

באמצעות הקואורדינטות a ו-b ניתן למצוא נקודה כלשהי על המפה (הנקודה שמחפשים מייצגת בדרך כלל מיקום של מקום שאותו אנו רוצים למצוא).

קואורדינטות יכולות להיות גם ביותר משני ממדים. לדוגמה, בשלושה ממדים, הנקודה (a,b,c), מורכבת משלושה חלקים:

a – קו הרוחב.
b – קו האורך.
c – הגובה.

לעיתים משתמשים במפות טופוגרפיות ברשת קואורדינטות שתי-וערב שרירותית, שלא מבוססת על קווי אורך ורוחב.

קואורדינטות במתמטיקה

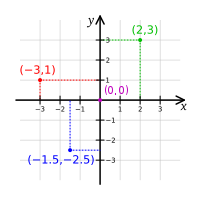
במתמטיקה, ובייחוד בגאומטריה יישומית, וכן בפיזיקה ובהנדסה, קואורדינטות או מערכת צירים היא מערכת בה לכל נקודה במרחב n-ממדי מותאמת קבוצה (סדורה) של מספרים (ברוב המקרים מדובר במספרים ממשיים, אך זה תלוי בהקשר). באופן פורמלי יותר, מערכת קואורדינטות על תחום X היא קבוצה (סדורה) של n פונקציות חלקות (כאשר n הוא ממד המרחב) מ-X אל הממשיים, כלומר:

\ \{x^{i}:X\to \mathbb {R} |i=1,...,n\ ;\ x^{i}\ {\mbox{ is smooth}}\}

או מנקודת מבט של אנליזה וקטורית,

\ (x^{1},\cdots ,x^{n}):X\to \mathbb {R} ^{n}

כך שהתאמה זו מהווה דיפאומורפיזם בין X לתת-תחום ב- $\mathbb {R} ^{n}$ .

אם המרחב הוא יריעה, ובפרט יריעה עקומה, לא תמיד ניתן למצוא מערכת קואורדינטות שתכסה באופן חלק את כל המרחב (אולם ניתן למצוא קבוצת מערכות קואורדינטות המכסות חלקים מהיריעה, שאפשר להדביק אותן באופן חלק באזורי החפיפה ביניהם). חבורות לי עוסקות, בין השאר, בקשר שבין מערכות הקואורדינטות בנקודות שונות של אותה יריעה.

במרחב אוקלידי, מערכת הקואורדינטות הבסיסית והטבעית ביותר היא קואורדינטות קרטזיות שמהווה גם בסיס ליניארי אורתונורמלי. זוהי מערכת הצירים הפשוטה והשימושית ביותר. במרחב אוקלידי מממד n, כל נקודה מתוארת באמצעות וקטור בעל n-רכיבים (במונחי תורת הקבוצות מדובר ב n-יה סדורה של n מספרים ממשיים), כאשר החיבור והכפל בסקלר מתבצעים רכיב-רכיב,

\ \mu \left(a_{1},\cdots ,a_{n}\right)+\lambda \left(b_{1},\cdots ,b_{n}\right)=\left(\mu a_{1}+\lambda b_{1},\cdots ,\mu a_{n}+\lambda b_{n}\right)

והמכפלה הפנימית היא המכפלה הסקלרית הסטנדרטית:

\ \left(a_{1},\cdots ,a_{n}\right)\cdot \left(b_{1},\cdots ,b_{n}\right)=a_{1}b_{1}+\cdots +a_{n}b_{n}=\sum _{i=1}^{n}{a_{i}b_{i}}

במערכת זו, וקטורי הבסיס הם מערכת אורתונורמלית קבועה שאיננה תלויה במיקום הנקודה במרחב. לכן אפשר להעתיק במערכת זו כל וקטור בצורה מקבילה לראשית. במרחבים כלליים יותר (ובפרט במרחבים עקומים) תכונה זו לא בהכרח נכונה.

התמרת קואורדינטות

אף על פי שכל מערכת קואורדינטות תקנית היא שימושית עבור חישובים נומריים במרחב נתון, המרחב עצמו קיים בנפרד מהקואורדינטות. למעשה, הקואורדינטות מהוות רק תיאור מסוים (ובמידה מסוימת, שרירותי) של המרחב, וישנן תכונות של המרחב שאינן תלויות במערכת הקואורדינטות שנבחרה לתאר אותו, תכונות אלה נקראות אינווריאנטים של המרחב והדרישה לשימורן במשוואות המערבות וקטורים וגדלים הקשורים למרחב מוליכה לעקרון הקו-ואריאנטיות ולפיתוחו של חשבון הטנזורים. בגישה המקובלת, מתייחסים להתמרת קואורדינטות כאל טרנספורמציה פסיבית. כלומר: איננו משנים את העצמים עצמם, אלא רק את הצורה (או הבסיס) שבה מתארים אותם.

יהי V מרחב וקטורי (אזי הוא בפרט תחום או יריעה) ונניח שבנינו מעליו 2 מערכות קואורדינטות שונות: $\ (x^{1},\cdots ,x^{n}){\mbox{ and }}(y^{1},\cdots ,y^{n})$ . למעשה, לכל נקודה (או וקטור) במרחב יש לנו שתי הצגות שונות. כל הצגה תלויה בבחירת הבסיס. נניח שאנו רוצים לעבור מהצגה אחת לשנייה. יהי v וקטור ב-V, אזי

\ {\vec {v}}=\sum _{i}{x^{i}{\hat {e}}_{(i)}}=\sum _{j}{y^{j}{\hat {f}}_{(j)}}

כאשר $\ \{{\hat {e}}_{(i)}\}_{i=1}^{n}$ ו $\ \{{\hat {f}}_{(j)}\}_{j=1}^{n}$ הם שני בסיסים שונים למרחב הווקטורי. נרשום את מטריצת המעבר ביניהם, M, באמצעות רכיביה: