סדרת פיבונאצ'י

בערך זה |
במתמטיקה, סדרת פיבונאצ'י (Fibonacci) היא הסדרה ששני איבריה הראשונים הם 1,1 וכל איבר לאחר מכן שווה לסכום שני קודמיו. בהתאם לכך, איבריה הראשונים של הסדרה הם:
איברי הסדרה נקראים "מספרי פיבונאצ'י".[1]
סדרת פיבונאצ'י קרויה על שם לאונרדו מפיזה (הידוע בכינוי "פיבונאצ'י"), שתיאר אותה לראשונה באירופה בספרו "ספר החשבונייה" בשנת 1202 (קדמו לו מתמטיקאים הודים). שם הסדרה הוענק לה על ידי אדוארד לוקאס. פיבונאצ'י השתמש בסדרה כדי לתאר את מספר הארנבים במשפחה של זוג ארנבים, אם מניחים שכל זוג ארנבים שהגיע לגיל חודשיים, ממליט מדי חודש זוג נוסף. באוכלוסייה כזו, מספר זוגות הארנבים בחודש ה-n (כולל ההורים) יהיה שווה ל- .
למעט הסדרות החשבוניות וההנדסיות, ושילובים שלהן, סדרת פיבונאצ'י היא הדוגמה הפשוטה ביותר לסדרה המוגדרת ברקורסיה. בניסוח פורמלי יותר, הגדרה רקורסיבית של הסדרה ניתנת על ידי תנאי ההתחלה , ונוסחת הנסיגה .
למספרי פיבונאצ'י יש תכונות רבות הנחשבות למעניינות. ספרים שלמים נכתבו עליהם ואף קיים כתב עת מתמטי, The Fibonacci Quarterly,[2] שמוקדש כולו לתגליות במספרי פיבונאצ'י והכללות שלהם. כמו כן, נוסדה אגודת פיבונאצ'י[3] שמטרתה לגלות מופעים חדשים של סדרת פיבונאצ'י.
סדרת פיבונאצ'י יוצרת גם את שבלול פיבונאצ'י, אם נצייר ריבועים שהצלעות שלהם הם מספרי פיבונאצ'י ונעביר קשתות בין קודקודיהם ייווצר שבלול המכונה שבלול פיבונאצ'י.[4]
מספרי פיבונאצ'י ויחס הזהב[עריכת קוד מקור | עריכה]
היחס בין שני איברים עוקבים של סדרת פיבונאצ'י שואף ליחס הזהב: מספר אי-רציונלי שערכו ...1.61803398, כפי שהראה לראשונה יוהאנס קפלר. יחס הזהב מושג בקירוב טוב כבר באיבר ה-11 של סדרת פיבונאצ'י:
ובאיבר ה-16 הדיוק משתפר לרמה של 5 ספרות אחרי הנקודה העשרונית:
תכונה זו אינה מפליאה אם מציגים את יחס הזהב כשבר המשולב: .
חלק סופי משבר אינסופי זה הוא יחס בין שני מספרי פיבונאצ'י עוקבים, אם קוטעים את החישוב במקום המתאים. לדוגמה, עבור האיברים 3 ו-5 השבר מקבל את הערך 1.666:
הצגה גאומטרית של מספרי פיבונאצ'י[עריכת קוד מקור | עריכה]




אחת מההצגות הגאומטריות של הסדרה מתחילה בריבוע שאורך צלעו 1, כגודל האיבר הראשון, ומתווספים לו ריבועים באופן הבא:
לריבוע הראשון מתווסף ריבוע נוסף בגודל 1x1. שני הריבועים יוצרים מלבן שרוחבו 1 ואורכו 2 - כגודל שני האיברים F2 ו-F3.
בשלב הבא נוסיף ריבוע בגודל 2x2, ונקבל מלבן בגודל 2x3. תוספת של ריבוע בגודל 3x3 תוביל למלבן בגודל 3x5. התוצר של הבנייה על ידי הוספת ריבוע שצלעו כאיבר פיבונאצ'י מביאה למלבן שצלעותיו הן שני איברי פיבונאצ'י עוקבים.
בהמשך הבנייה, המלבנים מתקרבים יותר ויותר למלבן הזהב, שהוא מלבן שהיחס בין צלעותיו הוא יחס הזהב - 1.618 בקירוב. ליחס הזהב ולמלבן הזהב מופעים שונים בטבע, באדריכלות ובאמנות.
תכונות נוספות של הסדרה[עריכת קוד מקור | עריכה]
זהות קאסיני[עריכת קוד מקור | עריכה]
את הזהות גילה האסטרונום האיטלקי ג'ובאני דומניקו קאסיני. הזהות אומרת כי , כלומר מספר פיבונאצ'י בריבוע הוא כמעט מכפלת שני המספרים לידו, ההפרש ביניהם הוא 1. מי גדול יותר זו שאלה שתלויה בזוגיות של המיקום של מספר הפיבונאצ'י שלקחנו. למשל, בסדרה יש את הרצף 3,5,8, שבו ו- וההפרש ביניהם הוא באמת 1. את הזהות ניתן להוכיח בכמה דרכים: דרך אחת היא באמצעות אינדוקציה מתמטית, שכן כך הסדרה מוגדרת. דרך אחרת היא להשתמש בעובדה שדטרמיננטה היא כפלית ולרשום:
סדרת לוקאס[עריכת קוד מקור | עריכה]
 ערך מורחב – סדרת לוקאס
ערך מורחב – סדרת לוקאס
סדרה דומה לסדרת פיבונאצ'י היא סדרת לוקאס. הסדרה מוגדרת על ידי:
סדרת פיבונאצ'י וסדרת לוקאס הן סדרות מהסוג הבא:
לכן .
ישנה עוד נוסחא המקשרת בין שתי הסדרות:
בנוסף, בדומה לנוסחא הכללית של סדרת פיבונאצ'י
גם לסדרת לוקאס יש נוסחא כללית:
תכונות מודולריות של סדרת פיבונאצ'י[עריכת קוד מקור | עריכה]
אחת הסיבות לחשיבותה של סדרת פיבונאצ'י בתורת המספרים היא ההתנהגות המעניינת של השאריות שלה בחלוקה למספר ראשוני קבוע. לדוגמה,
- כל מספר שלישי בסדרה הוא זוגי;
- כל מספר רביעי הוא כפולה של 3;
- כל מספר חמישי הוא כפולה של 5.
- כל מספר שביעי הוא כפולה של 13.
כאשר מתבוננים בסדרה מודולו כל מספר טבעי m, היא יכולה לקבל רק מספר סופי של ערכים, ולכן אין תימה שהסדרה מחזורית. כאשר בוחנים את הסדרה מודולו מספר ראשוני p, ישנם ארבעה מקרים: ראשית, מודולו p=2, סדרת השאריות היא ומחזורה 3. מודולו p=5 המחזור הוא 20. כאשר , המספר מקיים , כאשר המקדם הוא סימן יעקובי, השווה ל-1 אם 5 הוא שארית ריבועית מודולו p (זה קורה כאשר p מסתיים בספרות 1,4,6 או 9), ול־1- אחרת. אם 5 הוא שארית ריבועית אז וכן , וכך אפשר להוכיח שמחזור הסדרה מחלק את p-1. אם 5 איננו שארית ריבועית אז ו- , ובמקרה זה (החישוב נובע מן התכונה ), והמחזור מחלק את . תכונות אלה של סדרת פיבונאצ'י משמשות במבחני ראשוניות (ראו גם סדרת לוקאס).
לכל מספר טבעי m, אורך המחזור של סדרת פיבונאצ'י מודולו m הוא לכל היותר 6m. אורך המחזור הוא 6m אם ורק אם m שווה לכפליים חזקה של 5.
משפט זקנדורף[עריכת קוד מקור | עריכה]
 ערך מורחב – משפט זקנדורף
ערך מורחב – משפט זקנדורף
כל מספר טבעי ניתן להצגה בצורה יחידה כסכום של מספרי פיבונאצ'י שונים שאין ביניהם שניים עוקבים (סמוכים זה לזה בסדרה). הצגה זו נקראת הצגת זקנדורף, על שמו של הרופא הצבאי הבלגי אדואר זקנדורף (1901-1983), שהיה מתמטיקאי חובב והוכיח שהיא אכן תמיד קיימת.
את הצגת זקנדורף אפשר למצוא באמצעות אלגוריתם חמדן. מכיוון שכל מספר פיבונאצ'י עשוי להופיע בסכום לכל היותר פעם אחת, ההצגה המתקבלת נראית כמו הצגה בינארית: הספרה '1' במקום ה-n מסמנת שמספר פיבונאצ'י משתתף בסכום, וספרת '0' מציינת שהמספר אינו משתתף. למשל הצגת זקנדורף של מאה היא: .
חידות שסדרת פיבונאצ'י היא פתרונן[עריכת קוד מקור | עריכה]
בספר החשבונייה מספרי פיבונאצ'י מופיעים בהקשר לחידה העוסקת בארנבים. על-פי החידה זוג ארנבים צעיר הופך לאחר שנה לזוג ארנבים מבוגר. לצורך החידה הארנבים לא מתים אף פעם. זוג ארנבים מבוגר בכל שנה מוליד זוג ארנבים נוסף. מתחילים מזוג ארנבים צעיר אחד, כמה זוגות ארנבים יהיו מעתה כל שנה?
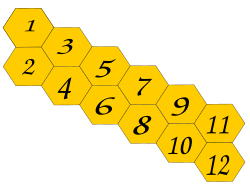
הפתרון לחידה הוא סדרת פיבונאצ'י. הסדרה מופיעה גם כפתרון לחידות קומבינטוריות רבות. לדוגמה, דבורה יכולה להיכנס לכוורת שבאיור דרך המשושה המסומן ב־1, או דרך המשושה המסומן ב־2. הדבורה יכולה לעבור ממשושה מסוים לשכנו, בתנאי שמספרו של המשושה החדש גדול ממספרו של המשושה בו היא נמצאת. בכמה דרכים שונות יכולה הדבורה להגיע למשושה ה־n?
חידה נוספת: אם אדם צריך לעלות בסולם n שלבים, וכל פעם עליו להחליט אם לעלות שלב אחד או שניים, כמה אפשרויות יש לו?
גם הפתרון לחידה זו הוא סדרת פיבונאצ'י, מפני שיש להסתכל על המהלך הראשון, במהלך הראשון יכול האדם לעלות שלב אחד או שניים, אם יעלה שלב אחד - אזי מספר האפשרויות הנותרות יהיה בדיוק כמספר האפשרויות לעלות n-1 שלבים, ואם יעלה 2 שלבים יהיה מספר האפשרויות הנותרות כמספר האפשרויות לעלות n-2 שלבים.
נוסחה ישירה לאברי הסדרה[עריכת קוד מקור | עריכה]
אפשר לקבל את אברי הסדרה בצורה ישירה על פי הנוסחה כאשר הם הפתרונות של המשוואה המאפיינת את יחס הזהב. יש המייחסים לאדוארד לוקאס את גילוי הנוסחה.[5] אולם הנוסחה הייתה ידועה כבר לז'אק פיליפ מארי בינה בשנת 1843,[6] ואולי אף ללאונרד אוילר ב-1765 ואפילו לאברהם דה-מואבר ב-1730.[7][8][9]
מכיוון ש- , מתקיים , ומכאן שהיחס בין אברי הסדרה שואף ליחס הזהב.
את הנוסחה קל להוכיח באינדוקציה. כדי לקבל אותה, כמו נוסחאות לסדרות רקורסיה ליניאריות אחרות, אפשר לכתוב את הגדרת הסדרה בעזרת מטריצה מתאימה:
מכיוון שהמשוואה האופיינית בלכסון המטריצה היא משוואת יחס הזהב, אפשר לכתוב:
והצבה בנוסחת הרקורסיה המטריציונית נותנת את הנוסחה הישירה עבור אברי הסדרה.
- ניתן להווכח בנכונות הנוסחה גם על ידי הנחה שכל חזקות יחס הזהב הם המספר בסדרה כפול יחס הזהב, ועוד המספר הקודם בסדרה.(שהרי יחס הזהב בריבוע הוא יחס הזהב ועוד 1) וכל הכפלה ביחס הזהב נותן את המספרים הבאים בסדרה.
- כעת אם תחבר את שני האיברים במונה תקבל את המספר בסדרה כפול 2 פעמים יחס הזהב פחות המספר בסדרה. ושורש של 5 הוא 2 פעמים יחס הזהב פחות 1.
שימושים במדעי המחשב[עריכת קוד מקור | עריכה]
ישנם אלגוריתמים ומבני נתונים כגון ערימת פיבונאצ'י המשתמשים בתכונות של מספרי פיבונאצ'י להוכחת סיבוכיות.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- מריו ליביו, חיתוך הזהב - קורותיו של מספר מופלא, הוצאת אריה ניר, 2003
- אלי מיטב, מספרים מכושפים - על חיתוך הזהב, סדרת פיבונאצ'י ועוד פנינים מתמטיות, הוצאת שורש, 2008
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מהילברט עד פיבונאצ'י, חידות המתבססות על סדרת פיבונאצ'י
- הרצאה "מהי מתמטיקה" של יונתן ברויאר - החל מדקה 33 הסבר מפורט ובסיסי על סדרת פיבונאצ'י, באתר יוטיוב
- סדרת פיבונאצ'י - סרטון הסבר של Vi Hart: חלק 1 חלק 2 חלק 3

- Sequences 3: Fibonacci – סרטון הסבר של MathTV על סדרת פיבונאצ'י (באנגלית)

- מחשבון לחישוב מספר פיבונאצ'י (באנגלית)
- מחשבון סדרת פיבונאצ'י (בעברית)
- פזיה מילר, סדרת פיבונאצ'י, באתר מכון דוידסון, יולי 2012
- יפעת אדלר בן יעקב, הקסם של מספרי פיבונאצ'י, באתר מכון דוידסון, דצמבר 2013
- יעל נוריק, מספרי פיבונאצ'י ויחס הזהב, באתר מכון דוידסון, מאי 2014
- סדרת פיבונאצ'י, באתר אנציקלופדיה למתמטיקה (באנגלית)
- קומפוזיציה בצילום - ספירלת פיבונאצ'י ויחס הזהב - באתר המרכז לצילום אומנותי, מאת גוסטבו הוכמן
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ (סדרה A000045 באתר OEIS – האנציקלופדיה המקוונת לסדרות של מספרים שלמים)
- ^ The Fibonacci Quarterly
- ^ The Fibonacci Association
- ^ הקסם של מספרי פיבונצ'י, באתר הקסם של מספרי פיבונצ'י
- ^ ביוגרפיה של סדרת פיבונאצ'י, באתר MacTutor (באנגלית)
- ^ Édouard Lucas, The Fibonacci Series
- ^ Binets Formula, באתר MathWorld (באנגלית)
- ^ Binet's, de Moivre's or Euler's Formula?
- ^ נוסחה באקסל לחישוב ערכי הסדרה:=1/(5^0.5)*((((1+5^0.5)/2)^A1)-(((1-5^0.5))/2)^A1) בטור A יש להציב את המספרים הסודרים, בטור B יתקבלו ערכי הסדרה























![{\displaystyle F_{n}={\frac {1}{\sqrt {5}}}\left[\left({\frac {1+{\sqrt {5}}}{2}}\right)^{n}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759d52bb949593bf6e6915d47ebd442eff8c1b7f)




















![{\displaystyle {\begin{pmatrix}1&1\\1&0\end{pmatrix}}^{n}=\left[{\frac {1}{\sqrt {5}}}{\begin{pmatrix}\phi _{+}&\phi _{-}\\1&1\end{pmatrix}}{\begin{pmatrix}\phi _{+}&0\\0&\phi _{-}\end{pmatrix}}{\begin{pmatrix}1&-\phi _{-}\\-1&\phi _{+}\end{pmatrix}}\right]^{n}={\frac {1}{\sqrt {5}}}{\begin{pmatrix}\phi _{+}&\phi _{-}\\1&1\end{pmatrix}}{\begin{pmatrix}\phi _{+}^{n}&0\\0&\phi _{-}^{n}\end{pmatrix}}{\begin{pmatrix}1&-\phi _{-}\\-1&\phi _{+}\end{pmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bff213f8b97027f6261e4f12cbb942fac232fb7a)