דטרמיננטה
באלגברה ליניארית, הדֵּטֶרְמִינַנְטָה של מטריצה ריבועית, היא סקלר התלוי ברכיבי המטריצה, ושווה לאפס אם ורק אם המטריצה אינה הפיכה.[1] יתרה מזו, כאשר הדטרמיננטה של מקדמי מערכת משוואות ליניאריות שונה מאפס, נוסחת קרמר מחשבת ממנה ומהדטרמיננטה של מטריצה קרובה, את הפתרון היחיד של המערכת. את הדטרמיננטה מסמנים או .
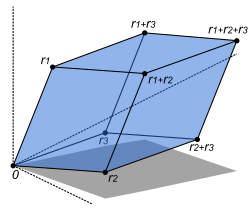
הדטרמיננטה היא פונקציה כפלית (כלומר, ), ובעלת משמעות גאומטרית: אם היא מטריצה ריבועית בעלת מקדמים ממשיים, אז הדטרמיננטה שלה שווה לנפחו (המכוון) של המקבילון (במרחב האוקלידי ה--ממדי), שקודקודיו הם עמודות המטריצה (בתמונה).
היסטוריה[עריכת קוד מקור | עריכה]
הדטרמיננטות מופיעות, בצורה לא מפורשת, כבר בלוחות חרס בבליים מן המאה השנייה לפני הספירה ואף לפני-כן, שם נעשה בהן שימוש לפתרון מערכות של שתי משוואות ליניאריות.
במאה ה-16 ניסח ג'ירולמו קרדאנו בעזרת דטרמיננטות את הפתרון למערכת של שתי משוואות בשני נעלמים; קרדנו הציג גרסה מוקדמת ולא מלאה של נוסחת קרמר, עבור מטריצות בגודל .
הנוסחה לדטרמיננטה של מטריצות גדולות יותר הופיעה באירופה וביפן בו זמנית, ב-1683. ביפן פרסם טאקאקזו סקי קווה (אנ') (1642-1708) הסבר על חישוב הדטרמיננטה של מטריצות מספריות מסדר המגיע עד , לצורך פתרון של משוואות שונות. באותה שנה, הציג לייבניץ את הנוסחה הכללית לחישוב דטרמיננטה מסדר , במכתב למרקיז דה לופיטל.
נוסחת קרמר הופיעה לראשונה, עבור מטריצות בגודל , בספר שפורסם ב-1748, כשנתיים לאחר מות המחבר קולין מקלורן. שנתיים אחר-כך פרסם גבריאל קרמר מאמר שבו תיאר בנספח, ללא הוכחה, את הכלל הקרוי על-שמו עבור מטריצות בגודל כלשהו.
לגראנז' הציג את הפירוש של דטרמיננטה (מסדר ) כאלמנט נפח, במאמר מ-1773 שעסק במכניקה. המונח דטרמיננטה מוצג לראשונה בספרו של גאוס על תורת המספרים; גאוס קרא לה כך משום שהיא קובעת (determines) את התכונות של התבניות הריבועיות שאותן חקר. עם זאת, הדטרמיננטה של גאוס אינה זהה להגדרה המקובלת היום. זו הופיעה בשם זה רק ב-1812, בעבודתו של קושי, שהוכיח לראשונה את הכלל החשוב .
הנושא הבשיל בשלושה מאמרים שפרסם יעקובי ב- 1841, בהם הוא הגדיר את הדטרמיננטה עבור מטריצה כללית ובאופן אלגוריתמי, שסייע לתפוצה הרחבה של הרעיון. את הסימון עבור הדטרמיננטה של הציע ארתור קיילי באותה שנה.
ב-1896 מיין פרדיננד פרובניוס את ההעתקות הליניאריות השומרות על הדטרמיננטה (במובן ש- לכל מטריצה ), והראה שכולן מהצורה או .
הגדרה "אקסיומטית", של הדטרמיננטה, כתבנית (היחידה) שהיא מולטי-ליניארית, אנטי-סימטרית ומנורמלת התגלתה על ידי קארל ויירשטראס, והתפרסמה ב-1903, לאחר מותו.
הגדרה[עריכת קוד מקור | עריכה]
הדטרמיננטה של מטריצה בגודל מוגדרת על-פי הנוסחה , כאשר .
הסכום בנוסחה הוא על התמורות האפשריות של המספרים . הסימן מתקבל על פי זוגיות התמורה. אם התמורה זוגית, , אם היא אי זוגית, . הדטרמיננטה שווה, אם כך, לסכום של כל המכפלות האפשריות לאורך אלכסונים מוכללים של המטריצה, עם סימנים מתחלפים.
לדטרמיננטה יש גם הגדרה אקסיומטית: אפשר לראות את הפונקציה כפונקציה של העמודות של המטריצה, ואז זוהי הפונקציה היחידה שהיא ליניארית בכל המשתנים, מתחלפת (כלומר מחזירה 0 עבור מטריצה שיש בה שתי שורות זהות), ומנורמלת כך ש- כאשר היא מטריצת היחידה. בלשון מודרנית, הגדרה זו שקולה לכך שפעולתה של טרנספורמציה ליניארית מממד על מכפלת היתד של המרחב (שהיא מרחב חד-ממדי) היא כפל בסקלר השווה לדטרמיננטה.
דוגמאות[עריכת קוד מקור | עריכה]
דטרמיננטיות 2X2[עריכת קוד מקור | עריכה]
במקרה של מטריצה , נוסחת הדטרמיננטה היא:
בפרט מתקיים:
ולכן מטריצה זו הפיכה.
לעומת זאת המטריצה הבאה איננה הפיכה:
כעת, חישוב הדטרמיננטה ייתן אפס:
- ולכן מטריצה זו אינה הפיכה.
דטרמיננטיות 3X3[עריכת קוד מקור | עריכה]
במקרה של מטריצה , נוסחת הדטרמיננטה היא:
הנוסחה כוללת 6 מחוברים (מפני שיש 6 תמורות באורך 3), 3 עם סימן חיובי ו-3 עם סימן שלילי.
חישוב הדטרמיננטה[עריכת קוד מקור | עריכה]
דירוג המטריצה[עריכת קוד מקור | עריכה]
הפיתוח לפי ההגדרה המפורשת דורש כ- פעולות בשדה. לעומת שיטות אלה, שיטת הדירוג של גאוס מאפשרת לחשב את הדטרמיננטה בכ- פעולות, על ידי דירוג המטריצה עד שמגיעים למטריצה משולשית: הדטרמיננטה של מטריצה משולשית שווה למכפלת איברי האלכסון הראשי שלה.
הדירוג נעשה על ידי הפעלת פעולות אלמנטריות בשרשרת, ואלו משפיעות על הדטרמיננטה באופן הבא:
- החלפת מקומן של שתי שורות (או עמודות) במטריצה משנה את סימן הדטרמיננטה: אם התקבלה מהמטריצה על ידי החלפת שתי שורות, אז .
- הוספה של כפולה בסקלר של שורה (עמודה) אחת לשורה (עמודה) אחרת אינה משנה את ערך הדטרמיננטה של המטריצה המתקבלת.
- הכפלה של שורה (או עמודה) במטריצה בסקלר מכפילה את ערך הדטרמיננטה של המטריצה באותו סקלר: אם התקבלה מהמטריצה על ידי הכפלת שורה כלשהי בסקלר , אז .
פיתוח לפי מינורים[עריכת קוד מקור | עריכה]
את הדטרמיננטה אפשר לחשב בצורה רקורסיבית, הנקראת פיתוח לפי מינורים. הדטרמיננטה של מטריצה בגודל הוא האיבר היחיד שלה. כעת נראה כיצד ניתן לחשב דטרמיננטה מסדר כאשר . המינור של איבר במטריצה הוא הדטרמיננטה של המטריצה המתקבלת על ידי מחיקת השורה והעמודה של אותו איבר מהמטריצה, כך שמתקבלת מטריצה בגודל (את הדטרמיננטה הזו, של מטריצה קטנה יותר, אנו כבר יודעים לחשב). נסמן את המינור המתקבל ממחיקת הרכיב (שהוא הרכיב ה- של המטריצה) ב-. הדטרמיננטה ניתנת כעת לחישוב בצורה -- זהו פיתוח לפי השורה ה-. פיתוח לפי העמודה ה- מתקבל מנוסחה דומה: .
לדוגמה, הפיתוח לפי השורה הראשונה של מטריצה מסדר נותן את הנוסחה .
הסיבוכיות בשיטה זו דומה לחישוב הדטרמיננטה על-פי ההגדרה, ולכן אין לה ערך מעשי, אלא אם יש במטריצה שורה או עמודה שכמעט כולה אפסים. עם זאת יש בה תועלת תאורטית לא מבוטלת. לדוגמה, נובע ממנה בקלות (באינדוקציה) שהדטרמיננטה של המטריצה המשוחלפת שווה לזו של המטריצה המקורית.
תכונות[עריכת קוד מקור | עריכה]
- הדטרמיננטה כפלית, כלומר . לכן גם:
- , כאשר סקלר ו- הוא סדר המטריצה של .
- , אם מטריצה הפיכה.
- , כאשר טבעי.
- , כאשר היא המטריצה המשוחלפת של .
- אם ורק אם מטריצה שאינה הפיכה.
- כאשר היא המטריצה המצורפת של ו- הוא סדר המטריצה של .
משפט סילבסטר קובע שלכל שתי מטריצות ו- מתקיים השוויון .
הפירוש הגאומטרי של הדטרמיננטה[עריכת קוד מקור | עריכה]
ניתן לראות בדטרמיננטה פונקציה של איברי המטריצה שערכה מבטא את פקטור ההגדלה הנפחית של הטרנספורמציה הליניארית המיוצגת על ידי המטריצה.
בצורה פורמלית, אם היא מטריצה ממשית מסדר , אז כפל המטריצה בוקטורי הבסיס הסטנדרטי של המרחב ייתן את ווקטורי העמודה של המטריצה:
פירוש הדבר הוא שהטרנספורמציה המיוצגת על ידי מעתיקה את קוביית היחידה ה-n ממדית למקבילון ה- ממדי שקואורדינטות קודקודיו מיוצגות על ידי ווקטורי העמודה של המטריצה , ואשר הפנים שלו מוגדר על ידי התחום: . הדטרמיננטה תיתן את הנפח המכוון של המקבילון הזה, כלומר (הסימן מראה האם הטרנספורמציה הליניארית משמרת או הופכת את אוריינטציית המקבילון[2]).
ניתן להיווכח בכך שהדטרמיננטה מקיימת את כל התכונות הנדרשות מפונקציית נפח - שכן פעולות אלמנטריות משנות את הדטרמיננטה באופן זהה לשינוי שהן גורמות לנפח המקבילון. הפעולה האלמנטרית של כפל שורה בסקלר שקולה להארכת אחת מצלעות המקבילון פי אותו פקטור; הפעולה מגדילה את שטח הפאה המכילה את הצלע באותו פקטור, ובאופן רקורסיבי פועלת כמתיחה בפקטור על פנים המקבילון, באנלוגיה להליך חישוב הדטרמיננטה לפי מינורים. הוספת כפולה של שורה לשורה אחרת ניתנת לייצוג על ידי כפל במטריצה אלמנטרית השקולה להעתקת גזירה, ולכן פועלת כטרנספורמציה אשר משנה את זוויות המקבילון אך אינה משפיעה על נפחו (ככל גזירה).
בדרך זו ניתן גם להבין את מושג ההפיכות של מטריצה בצורה שונה; מטריצה מסדר בעלת דטרמיננטה אפס מעתיקה את קוביית היחידה ה- ממדית למקבילון בעל נפח 0 שאינו יכול להיות -ממדי, מה שמעיד על כך שממד התמונה של נמוך מ-. פירוש הדבר הוא ש- מייצגת טרנספורמציה ליניארית שאינה על ואינה חד-חד ערכית, ולכן אין לה מטריצה הופכית (אין טרנספורמציה הופכית לטרנספורמציה שהיא מייצגת).
הדטרמיננטה באנליזה ווקטורית[עריכת קוד מקור | עריכה]
בשל הפירוש הגאומטרי של הדטרמיננטה שצוין לעיל, אם קבוצה כלשהי במרחב הממשי , אז הנפח של שווה לנפח של מוכפל בדטרמיננטה של (עובדה המסבירה את הופעתו של היעקוביאן בחישובי אינטגרלים מרובים).
- באמצעות דטרמיננטה של מטריצה אפשר לרשום ביטוי שקל לזכור ומקל לחשב את המכפלה הווקטורית ב- באופן הבא:
הדטרמיננטה כפונקציית נפח[עריכת קוד מקור | עריכה]
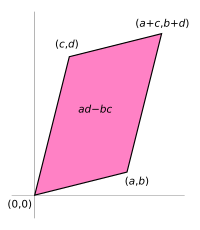
כפי שראינו עבור מטריצה ממשית ריבועית מסדר 2, הדטרמיננטה שלה מייצגת את השטח של המקבילית הנפרשת על ידי ווקטורי השורות של A (או עמודותיה). למעשה, הגדירו את הדטרמיננטה של מטריצה כפונקציה שמקבלת מטריצה ומחזירה את "השטח המכוון" של המקבילון הנפרש על ידי השורות (עמודות) שלה. מי אמר שיש פונקציה יחידה כזאת? כפי שנראה, יש רק דרך אחת להגדיר פונקציה נפח וזאת הגדרת הדטרמיננטה שאותה אנו מכירים.
הגדרה[עריכת קוד מקור | עריכה]
יהי שדה ותהי . נאמר ש- פונקציית נפח אם ורק אם
- ליניארית בכל אחד מהמשתנים (מולטי - ליניאריות).
- לכל , אם שניים מהם שווים אז .
- כאשר הם איברי הבסיס הסטנדרטי של .
(מן הליניאריות והתכונה השנייה נובע שאם B מתקבלת מ-A על ידי החלפת שתי שורות, אז ).
נרשה לעצמנו להסתכל על איברים מ- כאל איברים מ- כך שכל מטריצה מיוצגת כאל -יה של ווקטורי השורות שלה. כך, נוכל להסתכל על כל פונקציית נפח כאל פונקציה מ- ל- באופן שתיארנו.
הוכחה[עריכת קוד מקור | עריכה]
נסמן את שורותיה של ב- (בהתאמה) ושל ב- (גם בהתאמה). נניח ש- התקבלה מ- על ידי החלפת השורה ה- עם ה- .
כעת בהינתן פונקציית נפח ומטריצה ריבועית מסדר , מעל שדה שאת שורותיה נסמן ב- בהתאמה
ומתכונה 2 של פונקציית הנפח ניתן להיווכח כי מספיק לסכום על אוסף התמורות -
(*) - מחליפים שורות עד שמגיעים לרצף ועם כל החלפה כופלים במינוס 1. מתכונות התמורה הוא מספר ההיפוכים של ולכן,
ובכך הוכח כי פונקציית נפח היא יחידה.
עדיין לא הוכח שבכלל קיימת פונקציית נפח. ההוכחה מסורבלת אבל ניתן להוכיח שלכל טבעי קיימת פונקציית נפח יחידה . ואם לכל
כאשר היא המטריצה המתקבלת מ- על ידי מחיקת השורה ה- והעמודה ה- .
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- היסטוריה של מטריצות ודטרמיננטות
- גדי אלכסנדרוביץ', דטרמיננטות, באתר "לא מדויק"
- סרטונים המדגימים חישוב דטרמיננטה: פיתוח דטרמיננטה לפי שורה ראשונה ופיתוח דטרמיננטה לפי חוק סארוס
- דטרמיננטה, באתר אנציקלופדיה למתמטיקה (באנגלית)
- דטרמיננטה, באתר MathWorld (באנגלית)
- דטרמיננטה, באתר אנציקלופדיה בריטניקה (באנגלית)
 גורמים, דף שער בספרייה הלאומית
גורמים, דף שער בספרייה הלאומית
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ בדיקת ערך הדטרמיננטה של המטריצה של העתקה ליניארית, היא שיטה אלגוריתמית לוודא האם העתקה הפיכה.
- ^ שיקופים למשל, בשונה מסיבובים, אינם משמרים אוריינטציה של המקבילון.
| נושאים באלגברה ליניארית | ||
|---|---|---|
| מושגי יסוד | שדה • מרחב וקטורי • משוואה ליניארית • מערכת משוואות ליניאריות • העתקה ליניארית • מטריצה | |
| וקטורים | סקלר • כפל בסקלר • צירוף ליניארי • תלות ליניארית • קבוצה פורשת • בסיס • וקטור קואורדינטות • ממד | |
| מטריצות | כפל מטריצות • שחלוף • דטרמיננטה • דירוג מטריצות • דרגה • עקבה • מטריצה מצורפת • מטריצת מעבר • מטריצה משולשית • דמיון מטריצות • ערך עצמי • פולינום אופייני • לכסון מטריצות • צורת ז'ורדן | |
| העתקות | העתקה ליניארית • קואורדינטות • מטריצה מייצגת • גרעין • אנדומורפיזם • איזומורפיזם • העתקה אפינית • העתקה פרויקטיבית | |
| מרחבי מכפלה פנימית | מכפלה סקלרית • מכפלה וקטורית • אורתוגונליות • מטריצה סימטרית • אופרטור הרמיטי • אופרטור אוניטרי • טרנספורמציה נורמלית • נורמה • מטריקה | |
| תבניות | תבנית ביליניארית • תבנית סימטרית • תבנית הרמיטית • תבנית סימפלקטית • חפיפת מטריצות • משפט סילבסטר • תבנית מולטי-ליניארית אנטי-סימטרית • אוריינטציה • צפיפות • טנזור | |















































































































