יחס הזהב

יחס הזהב (או חיתוך הזהב) הוא קבוע מתמטי המעסיק את המדע והאמנות כבר מאות שנים. זהו מספר אי רציונלי המסומן באות היוונית פי ( ולעיתים ): .
יחס הזהב הוא הפתרון החיובי של המשוואה:
לפי ההשערות, יחס זה התגלה על ידי אחד מתלמידיו של פיתגורס; הוא תואר בספרו של אוקלידס, "יסודות", לפני כ-2,300 שנים. לוקה פאצ'ולי, מתמטיקאי איטלקי מתקופת הרנסאנס, הקדיש ליחס הזהב ספר שלם, וכינה אותו "הפרופורציה האלוהית".
היחס מייצג מידות וגדלים רבים בטבע, והחל מתקופת יוון הקלאסית, הוא גם משמש באמנות ובאדריכלות. את האות פי לתיאור היחס הציע המתמטיקאי האמריקני מארק באר.
| בינארי | 1.1001111000110111011... |
| עשרוני | 1.6180339887498948482... |
| הקסדצימלי | 1.9E3779B97F4A7C15F39... |
| שבר משולב | |
| ייצוג אלגברי | |
| טריגונומטריה |
הגדרות מתמטיות[עריכת קוד מקור | עריכה]
הצגה גאומטרית של ההגדרה[עריכת קוד מקור | עריכה]
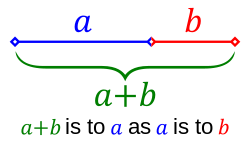
שני גדלים a ו-b מקיימים את יחס הזהב אם היחס בין סכום הגדלים לבין הגדול מביניהם שווה ליחס שבין הגדול מביניהם לקטן מביניהם. בנוסחה:
באותה מידה, יחס הזהב מתקיים כאשר היחס בין הגדול לקטן שווה ליחס שבין הקטן לבין הפרש הגדלים. בנוסחה:
בהתקיים שוויון זה, היחס בין הגדלים האמורים שווה ליחס הזהב:
הצגה אלגברית של ההגדרה[עריכת קוד מקור | עריכה]

אם נסמן את יחס הזהב ב-, נקבל את המשוואה האלגברית , הנגזרת מהדרישה שלעיל, או באופן שקול, מ-. משוואה זו שקולה למשוואה הריבועית , שלה פתרון חיובי ופתרון שלילי. הפתרון החיובי הוא
זהו המספר הממשי החיובי היחיד שמקיים את המשוואה הריבועית לעיל.
תכונות מתמטיות של יחס הזהב[עריכת קוד מקור | עריכה]
- יחס הזהב הוא מספר אי רציונלי. עובדה זו נובעת מכך שהמספר הוא אי רציונלי.
- ההופכי של יחס הזהב הוא בקירוב 0.618. זהו הערך המוחלט של השורש השלילי של המשוואה הריבועית לעיל, והוא גם שווה ליחס הזהב פחות יחידה.
- הריבוע של יחס הזהב הוא בקירוב 2.618 - הוא עצמו ועוד יחידה.
כמו כן, יחס הזהב שווה לשני הביטויים הבאים:
- השורש החוזר
- השבר המשולב
- תכונותיו של יחס הזהב מקבלות ביטוי בזוויות מסוימות (עשירית או חמישית ממחצית העיגול) המתקשרות לתכונות של מחומשים (ראו בהמשך):
יחס הזהב וסדרת פיבונאצ'י[עריכת קוד מקור | עריכה]
 ערך מורחב – סדרת פיבונאצ'י
ערך מורחב – סדרת פיבונאצ'י

סדרת פיבונאצ'י היא סדרת מספרים ששני איבריה הראשונים שווים ל-1, ולאחר מכן כל איבר בסדרה הוא סכום של שני האיברים הקודמים לו. תחילתה של הסדרה היא המספרים 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. (יש המגדירים את הסדרה כמתחילה במספר 0). נהוג לסמן ב- את האיבר ה-n בסדרה. יוהאנס קפלר הראה שהמנה של כל שני איברים עוקבים בסדרת פיבונאצ'י שואפת ליחס הזהב. עם זאת, גם אם נחשב את היחס בין שני איברים עוקבים גדולים מאוד בסדרה, לעולם לא נקבל בדיוק את יחס הזהב, משום שכאמור, יחס זה אינו מספר רציונלי. תכונה זאת אינה מיוחדת לסדרת פיבונאצ'י דווקא, אלא כל סדרה רקורסיבית בעלת התנאי , לכל תנאי התחלה, היחס שואף ליחס הזהב ככל ש-n גדל.
אחת ההצגות הגאומטריות של הסדרה מתחילה בריבוע שאורך צלעו 1, כגודל האיבר הראשון. לריבוע זה מוצמד ריבוע נוסף בגודל 1x1, כך ששני הריבועים יוצרים מלבן שרוחבו 1 ואורכו 2, כגודל שני האיברים ו-. בשלב הבא נצמיד למלבן ריבוע בגודל 2x2, ונקבל מלבן חדש בגודל 2x3. תוספת של ריבוע בגודל 3x3 תיצור מלבן בגודל 3x5, וכך הלאה. בכל שלב, ההוספה של ריבוע שאורך צלעו הוא האיבר הבא בסדרת פיבונאצ'י יוצרת מלבן שאורכי צלעותיו הם שני איברי פיבונאצ'י עוקבים. המלבנים המתקבלים מתקרבים יותר ויותר למלבן הזהב - מלבן שהיחס בין צלעותיו הוא יחס הזהב.
יחס הזהב מושג בקירוב טוב כבר באיבר ה-11:
באיבר ה-16, הדיוק משתפר:
חזקות[עריכת קוד מקור | עריכה]
חזקות טבעיות של יחס הזהב ניתנות להבעה על ידי צירופים של מספרי פיבונאצ'י, בצורה הכללית הבאה:
כך מתקבל
סדרות נוספות הקשורות ליחס הזהב[עריכת קוד מקור | עריכה]
סדרה נוספת הקשורה ליחס הזהב היא סדרת מספרי לוקאס, הנפתחת במספרים 2,1 וממשיכה כסדרת פיבונאצ'י כך שכל מספר הוא סכום שני הקודמים לו:
- 2,1,3,4,7,11,18,29,47,76...
סדרה זו ידועה בכך ש- ככל ש-n גדל. למשל: ואילו .
גאומטריה של יחס הזהב[עריכת קוד מקור | עריכה]
מלבן הזהב[עריכת קוד מקור | עריכה]

מלבן הזהב הוא מלבן שהיחס בין צלעותיו הוא יחס הזהב.
תכונתו המיוחדת של מלבן הזהב היא שהוספת ריבוע אליו יוצרת מלבן זהב חדש. נראה זאת: אם נוסיף למלבן הזהב שמשמאל את הריבוע שצלעו a, נקבל מלבן חדש שצלעותיו הן a ו-a+b, שהיחס ביניהן הוא יחס הזהב - , זאת מאחר שאם

1. בנה ריבוע שצלעו יחידה (מודגש באדום).
2. חצה אותו לשני מלבנים.
3. השתמש באלכסון של אחד המלבנים בתור רדיוס לבניית מלבן הזהב
.
- הרי ש-
- או (על פי תכונתו של יחס הזהב לעיל)
כלומר היחס בין a+b ל-b הוא יחס הזהב בריבוע, אך היחס בין a ל-b הוא יחס הזהב, ולכן גם היחס בין a+b ל-a הוא יחס הזהב, שכן .
קיימת טענה כי היוונים הקדמונים והמצרים הקדמונים התייחסו אל יחס הזהב כאל יחס אסתטי במיוחד, ולכן ניתן למצוא יחס זה במבנים מהעולם העתיק, כגון הפרתנון באתונה, וביצירות אמנות. השימוש ביחס הזהב, ככל שהוא קיים בתחומים אלה, מתבטא בעיקר באמצעות מלבן הזהב.
יחס הזהב, מחומשים ופנטגרמים[עריכת קוד מקור | עריכה]
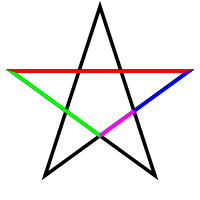
• היחס בין הקטע האדום לקטע הירוק שווה ליחס הזהב,
• כמו גם היחס בין הקטע הירוק לקטע הכחול,
• והיחס בין הקטע הכחול לקטע הסגול.
למחומש משוכלל ולפנטגרם תכונות הקושרות אותם במישרין ליחס הזהב.
אם נמתח אלכסונים בתוך מחומש משוכלל, נקבל פנטגרם, ובמרכזו של כל פנטגרם נקבל מחומש משוכלל חדש, וכך ניתן להמשיך את הסדרה עד אינסוף. גודלה של זווית פנימית במחומש משוכלל הוא 108 מעלות, ולכן הזווית בכל אחד מקודקודי הפנטגרם היא בת 36 מעלות.
- (במשולש שווה-שוקיים שקודקדו 36 מעלות ניתן להוכיח שהיחס קיים בין השוקיים לבסיס על ידי דמיון משולשים)
הפנטגרם הוא אחת מהצורות הגאומטריות שבהן מתגלה באופן טבעי יחס הזהב. בפנטגרם מתחלקות הצלעות המרכיבות אותו למספר קטעי צלעות באורכים שונים. היחס בין כל שני אורכים עוקבים שווה ליחס הזהב. סוברים[1], כי תוך התבססות על קשר זה, הוכיחו הפיתגוראים כי אין מידה משותפת לצלע ולאלכסון של המחומש (כלומר מדובר ביחס שהוא מספר אי רציונלי) - מה שמתקשר להיותו של יחס הזהב מספר אי רציונלי. על כך נסמכת טענה נוספת - מי שגילה את יחס הזהב היו כבר הפיתגוראים.
זווית הזהב[עריכת קוד מקור | עריכה]

אם נחלק את המעגל (360 מעלות) ביחס הזהב, נקבל זווית בת כ-°222.5. הזווית המשלימה זווית זו ל-360° נקראת זווית הזהב והיא שווה בקירוב ל-137.5°.
זווית הזהב היא:
תצפיות של חוקרים על נביטת עלי צמחים הראו שעלים חדשים נוטים להופיע בזווית זו על הגבעול.
יחס הזהב ויחסים אחרים[עריכת קוד מקור | עריכה]
יחס הזהב הוא המוכר בסדרה של יחסים, או קבועים מתמטיים, הנקראים ממוצעי הכסף (silver means), ששוויים הוא פונקציית הזהב:
יחס הזהב מתקבל עבור n=1 ואילו עבור n=2 מתקבל קבוע הנקרא יחס הכסף. יחסים נוספים מובאים בטבלה משמאל. היחסים הללו פותרים את המשוואה הריבועית
| קבועי הכסף | ||
| 0: | (0 + 4√)½ | 1 |
| 1: | (1 + 5√)½ | 1.618033989 |
| 2: | (2 + 8√)½ | 2.414213562 |
| 3: | (3 +13 √)½ | 3.302775638 |
| 4: | (4 + 20√)½ | 4.236067978 |
| 5: | (5 +29√)½ | 5.192582404 |
| 6: | (6 + 40√)½ | 6.162277660 |
| 7: | (7 + 53√)½ | 7.140054945 |
| 8: | (8 +68√)½ | 8.123105626 |
| 9: | (9 +85√)½ | 9.109772229 |
| ... | ||
| n: | ||
ושווים גם לביטוי:
סדרה בעלת מיקום סידורי m שבה האיבר האפסי הוא 0, האיבר הראשון הוא 1 והיחס בין שני איבריה העוקבים שואף לממוצע הכסף , היא בעלת הנוסחה הסגורה:
עבור n=1 מתקבלת הנוסחה הסגורה לסדרת פיבונאצ'י, ואילו עבור n=2 מתקבלת הנוסחה הסגורה לסדרת פל. עבור המספר n, החוקיות של הסדרה היא שכל איבר שווה ל-n פעמים כפול האיבר הנמצא מקום אחד לפניו, ועוד האיבר הנמצא שני מקומות לפניו. כלומר:
תחומים בהם מופיע יחס הזהב[עריכת קוד מקור | עריכה]
יחס הזהב קיבל הילה מיסטית מסוימת, עד כדי כינויו בשם "הפרופורציה האלוהית" בספרו של פאצ'ולי. מנגד, נמצא ב-1994 שוויון המקשר את יחס הזהב דווקא למספר החיה (666) - מספרו של האנטיכריסט:
בעוד שאין חולק על תכונותיו המתמטיות המיוחדות של המספר, רבים רואים בנטייה לחפש את היחס בתחומים מסוימים כאדריכלות ואמנות כנטיית לבם של חסידי המספר ותו לא, וזאת מהטעם שערכו של המספר קרוב מאוד לשבר העשרוני 1.6. יחס הזהב מופיע, או נטען ככזה, בתחומים הבאים:
- בגאומטריה: בפנטגרמים ומחומשים, במלבני זהב ובמשולשי זהב.
- בבוטניקה: בסידור העלים סביב הגבעול, במיקום הזרעים בתפוח, באיצטרובל של אורן, בהיערכות זרעי החמנייה בתפרחת, בעלי הכותרת בוורד.
- בתצורות של גבישים: על גילוי גביש כמו-מחזורי מחומש המקיים את יחס הזהב זכה פרופ' דן שכטמן בפרס נובל לכימיה לשנת 2011[2]
- בדגלי מדינות
- בבעלי חיים: בקרני צבאים, ביחס בין הדבורים בכוורת, ובצורה הלוליינית של קונכיית הנאוטילוס (אם כי יש הרואים בכך מיתוס ותו לא[3])
- באמנות
- באדריכלות: למשל במבנה מוזיאון גוגנהיים, או במטה האומות המאוחדות
- בניתוח טכני של שוק המניות (בהתבסס על סדרת פיבונאצ'י)
- בהליכים מסוימים בפסיכולוגיה.[דרוש מקור]
- באנליזה נומרית - סדר ההתכנסות של שיטת המיתר (secant) הוא יחס הזהב.
- במעגלים חשמליים - ההתנגדות השקולה של שרשרת נגדים אינסופית בערך של 1 אוהם המחוברים לסירוגין בטור ובמקביל שווה ליחס הזהב[4].
מלבן הזהב באמנות ובאדריכלות[עריכת קוד מקור | עריכה]



יצירות אמנות חזותיות ואדריכליות משמשות את חסידי יחס הזהב ככר פורה. ברוב המקרים קשה להוכיח או להפריך את הטענות בדבר שימוש ביחס הזהב, הן בשל בעיות מדידה (וקרבתו של היחס למספר 1.6), והן בשל היעדר כל תיעוד.
נטען כי השימוש ביחס הזהב החל כבר באדריכלות של יוון הקלאסית. מבנים קלאסיים כגון הפרתנון באתונה נבנו ביחס קרוב ליחס הזהב, אם כי יש מומחים המפקפקים בכך[5] וטוענים, כי מדידת הפרתנון עשויה להיערך בכל מיני צורות, והאומדן כי יחס הזהב היה מעורב בבנייה היא שרירותית.
יש הטוענים[דרוש מקור] שאת יחס הזהב ניתן לראות גם במבנה הפירמידה הגדולה של גיזה, בה היחס בין גובה הפירמידה לבסיסה הוא 1.618. כמו כן, יחס הגבהים בין הראש לרגל לבין המרחק מהטבור לרגל הוא 1.618.
יש המנסים לראות את יחס הזהב גם בממדיו של ארון הברית, שבהתאם להוראות הבנייה, אורכו אמתיים וחצי, ורחבו אמה וחצי.[6]. כלומר יחס של 1.666, שהוא הקירוב הטוב ביותר ליחס הזהב לאור העובדה שתכנון המשכן נמסר באמות שלמות או חצויות בלבד.[7]
בימי הביניים נעשה שימוש ביחס הזהב באדריכלות האסלאמית. לדוגמה, כיפת הסלע בירושלים נבנתה במידות פרופורציונליות מדויקות התואמות את יחס הזהב[8], אם כי קיים קושי להראות כי אכן מדובר ביחס הזהב.
יש הסבורים כי יחס הזהב נחשב באמנות כפרופורציה המושלמת והיפה ביותר שאדם יכול לתאר. אמני הרנסאנס בתחום הציור, הפיסול והאדריכלות השתמשו בפרופורציות אלה כדי להשיג את מה שנחשב ליופי המושלם. פרופורציות של חתך הזהב ניתן למצוא בשפע בציוריו של לאונרדו דה וינצ'י ושל אמנים גדולים אחרים.
אנשי הרנסאנס פיירו דלה פרנצ'סקה ולוקה פאצ'ולי כתבו שניהם ספרים העוסקים ביחס הזהב. ספרו של פאצ'ולי "על הפרופורציה האלוהית" ("De divina proportione") נכתב במילאנו בשנים 1496–1498 ופורסם בוונציה ב-1509. את הספר אייר לאונרדו דה וינצ'י.
בציורו המפורסם של לאונרדו דה וינצ'י, המונה ליזה, ניתן למדוד יחס זהב מדויק בפני המונה ליזה. גם בציור "הירונימוס הקדוש" משנת 1483 השתמש דה וינצ'י ביחס הזהב. בציור מתואר הירונימוס הקדוש יושב ולמרגלותיו אריה. הירונימוס הקדוש עצמו תחום במלבן זהב. גם על טענות אלה קמו חולקים.
גם כיום משתמשים במלבן הזהב באדריכלות ובגרפיקה. מספר בניינים מודרניים נבנו בעולם לפי יחס הזהב. למשל, היחס בין גובהו (152 מטר) ורוחבו (95 מטר) של בניין המזכירות של האומות המאוחדות בניו יורק הוא היחס 1.621 שקרוב מאוד לחתך הזהב. כרטיסי אשראי וכרטיסים מגנטיים נוספים קרובים במידותיהם למלבן הזהב.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- אלי מיטב, מספרים מכושפים - על חיתוך הזהב, סדרת פיבונאצ'י ועוד פנינים מתמטיות, הוצאת שורש, 2008.
- מריו ליביו, חיתוך הזהב – קורותיו של מספר מופלא, הוצאת אריה ניר, 2003.
- מיכאל קוסטא, חתך הזהב, חותם שלמה ומגן דוד, ספרית פועלים, 1990.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- אתר העוסק ביחס הזהב, יישומיו ושאר הקשרים שונים
- אתר העוסק ביחס הזהב, כולל ערכו עד אלפי ספרות אחרי הנקודה העשרונית
- גילה בלס, חתך הזהב באמנות, מחשבות 59, אפריל 1990, עמ' 36–45
- יחס הזהב, באתר אנציקלופדיה למתמטיקה (באנגלית)
- יחס הזהב, באתר MathWorld (באנגלית)
- יחס הזהב, באתר אנציקלופדיה בריטניקה (באנגלית)
- מאמר של ליאור שמיר על חתך הזהב
- סדרת הספרות של יחס הזהב באתר OEIS – האנציקלופדיה המקוונת לסדרות של מספרים שלמים
 חתך הזהב, דף שער בספרייה הלאומית
חתך הזהב, דף שער בספרייה הלאומית
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ למשל, קורט פון-פריץ, במאמרו "גילוי חוסר המידה המשותפת בידי היפסוס ממטאפונטום" (1945 ,The Annals of Mathematics)
- ^ פרופ' מריו ליביו, תגלית הזהב: המתמטיקה שמאחורי הגבישים, באתר ynet, 5 באוקטובר 2011
- ^ John Sharp, Spirals and the Golden Section – Part 4: The Myth Of The Nautilus Shell, Nexus Network Journal, Winter 2002
- ^ Gary ZL1AN, The Infinite Resistor Chain, NZART Journal, 2007
- ^ George Markovsky, Misconceptions about the golden ratio, College Mathematics Journal 23 (1992)
- ^ שמות, כ"ה, 10
- ^ שם טוב גפן, הממדים הנבואה האדמתנות, ירושלים תשל"ד, עמ' 209. מאיר בר אילן, נומרולוגיה מקראית, רחובות תשס"ה, עמ' 51.
- ^ דורון חן, The design of the Dome of the Rock in Jerusalem, Palestine Exploration Quarterly 112, 1980, עמ' 41-50
| מספרים אי-רציונליים נודעים | ||
|---|---|---|
| מספרים אלגבריים | 2√ • 3√ • יחס הזהב 𝜑 • יחס הכסף δAg • היחס הפלסטי 𝜌 | 
|
| מספרים טרנסצנדנטיים | בסיס הלוגריתם הטבעי 𝑒 • פאי 𝜋 • קבוע גאוס • קבוע אומגה Ω • קבוע ליוביל | |
| מספרים אי-רציונליים, שלא ידוע האם הם אלגבריים או טרנסצנדנטיים |
קבוע אפרי (3)ζ • קבוע ארדש-בורוויין | |
| טריגונומטריה | קבועים טריגונומטריים מדויקים | |




















































![{\displaystyle \!\,{\frac {1}{\sqrt {n^{2}+4}}}\left[\left({\frac {n+{\sqrt {n^{2}+4}}}{2}}\right)^{m}-\left({\frac {n-{\sqrt {n^{2}+4}}}{2}}\right)^{m}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/920acfea71184b17814116c9e27a1585c4a35c26)

