מעגל RLC
מעגל RLC הוא מעגל חשמלי המורכב מנגד, משרן (נקרא גם סליל השראה או בקיצורו: סליל) וקבל המחוברים בטור או במקביל. אל המעגל ניתן לחבר מקור מתח או מקור זרם. מעגל RLC הוא מעגל תהודה חשמלי והוא מתאים לשמש כמסנן מעביר פס. מעגל RLC נקרא גם מעגל מסדר שני משום שניתן לתאר אותו בעזרת משוואה דיפרנציאלית ליניארית מסדר שני.
מעגל טורי ומעגל מקבילי[עריכת קוד מקור | עריכה]

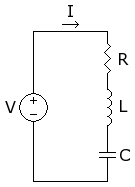
ניתן לחבר את רכיבי המעגל בטור או במקביל. המעגל הטורי והמעגל המקבילי הם מעגלים דואליים[דרושה הבהרה]. כמו כן, ניתן לחבר למעגל מקור מתח או מקור זרם. שני החיבורים שקולים זה לזה לפי משפט נורטון ומשפט תבנין, וגם הם מעגלים דואליים.
המשוואה הדיפרנציאלית המתארת את הזרם במעגל טורי המחובר למקור מתח היא:
כאשר R התנגדות הנגד, L השראות המשרן, C קיבול הקבל ו-V מתח המקור. אותה משוואה מתארת את הזרם דרך המשרן במעגל מקבילי המחובר למקור זרם, כאשר באגף ימין מתח המקור V מוחלף בזרם המקור.
העכבה השקולה של המעגל המקבילי:
העכבה השקולה של המעגל הטורי:
תהודה[עריכת קוד מקור | עריכה]
 ערך מורחב – מעגל תהודה חשמלי
ערך מורחב – מעגל תהודה חשמלי
המשוואה הדיפרנציאלית המתארת את המעגל היא משוואת מתנד הרמוני:
לכן תגובת ההלם של המעגל, או התגובה שלו לתנאי התחלה, מתנודדת בתדירות התנודה העצמית שלו. מלבד זאת, בעת כניסה סינוסית בתדירות זו תתרחש תהודה ולכן תדירות התנודה העצמית נקראת גם תדירות התהודה. ניתן לזהות את תדירות התהודה הבלתי מרוסנת מהמשוואה הדיפרנציאלית: . תהודה תתרחש כאשר האימפדנס של המעגל המקבילי מקסימלי וזה של הטורי מינימלי. בשני המקרים תדירות התהודה היא:
ברוב מעגלי התהודה החשמליים וכתוצאה מכך . כלומר אם נחבר קבל טעון למשרן ולנגד, כל הזרמים והמתחים במעגל יהיו בצורת סינוס בתדירות התנודה העצמית עם משרעת שדועכת בזמן. אם נחבר את המעגל למקור זרם או למקור מתח שמזרימים זרם חילופין, המתחים במעגל יהיו בצורת סינוס באותה התדירות של המקור אך בעלי משרעת שונה, שתהיה מקסימלית עבור מקור בתדירות התהודה. הסיבה להנחתה בתדירויות נמוכות היא שהסליל מתנהג כקצר והקבל כנתק, ובתדירויות גבוהות משום שהסליל מתנהג כנתק והקבל כקצר.
מהמשוואה הדיפרנציאלית ניתן לזהות גם את מקדם הריסון - מדד לקצב הדעיכה של תגובת ההלם:
עבור חיבור מקבילי:
עבור חיבור טורי:
מקדם הריסון הוא היחס בין ההנחתה (המסומנת α) לתדירות התהודה:
עבור חיבור מקבילי:
עבור חיבור טורי:
את סוג הריסון של המעגל נקבע על פי ישנם חמישה סוגי ריסונים עבור מעגל RLC :
- ריסון יתר (או ריסון לא קריטי) - כאשר Δ > 0, הפונקציה יציבה אסימפטוטית, כלומר היא מתייצבת לאחר זמן והזרם מגיע ל-0.
- ריסון קריטי - כאשר Δ = 0, הפונקציה יציבה אסימפטוטית.
- תת-ריסון - כאשר Δ<0, הפונקציה יציבה אסימפטוטית.
- כאשר R=0 וכפועל יוצא α=0 - הפונקציה אינה יציבה אסימפטוטית, כלומר היא איננה מתייצבת לאחר זמן מכיוון שאין נגד ש'ייקח' מתח, והמתח עובר בין הסליל לקבל בלי הפסקה.
- כאשר R<0 (יכול לקרות במקור תלוי למשל) - הפונקציה אינה יציבה אסימפטוטית, והיא עולה בצורה אקספוננציאלית עד שהמערכת עלולה להתפוצץ ולהתפרק.
שימושים[עריכת קוד מקור | עריכה]
כאשר מעגל RLC משמש כמתנד, בדרך כלל יש צורך במקדם ריסון ובהנחתה נמוכים. ניתן לעשות זאת על ידי התנגדות קטנה במעגל טורי והתנגדות גדולה במעגל מקבילי, ובמקרה כזה המעגל דומה למעגל LC.
מעגל RLC מתאים לשמש כמסנן מעביר פס משום שהוא מגביר תחום תדרים סביב תדר התהודה ומנחית את כל היתר. את תדר התהודה ניתן לקבוע על ידי L ו-C, ולשנות אותו בעזרת קבל משתנה או משרן משתנה. כך משמש מעגל RLC במקלט רדיו - שינוי הקיבול מאפשר להאזין לתדרים שונים.
רוחב הסרט הוא תחום התדרים שבו ההספק מוגבר בלפחות חצי מהגברו בתדר התהודה, והוא שווה:
מקדם האיכות של מעגל RLC טורי הוא:
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
| חשמל | ||
|---|---|---|
| מושגי יסוד | מטען • שדה חשמלי • אנרגיה פוטנציאלית חשמלית • פוטנציאל • מתח • כא"מ • זרם • התנגדות ומוליכות • עכבה • הספק • השראות • זרם ישר • זרם חילופין • מעגל חשמלי • תהודה • עכבה אופיינית | 
|
| רכיבים בסיסים | מקור מתח • מקור זרם • נגד • קבל • משרן • ממריסטור • שנאי • מפסק • מבדד | |
| מכשירי מדידה | מד מתח • מד זרם • מד התנגדות • אלקטרוסקופ • גלוונומטר • מד קיבול • מד השראות • רב מודד • אוסצילוסקופ • מחולל אותות | |
| אלקטרוניקה | מוליך למחצה • דיודה • טרנזיסטור • מיתוג • שפופרת ריק • טריודה • דיודה פולטת אור (לד) • מגבר שרת • מסנן תדרים • מעגל משולב • מעגל מודפס • VLSI • מיקרואלקטרוניקה | |
| זרם חזק | גנרטור חשמלי • מנוע חשמלי • תחנת כוח • מתקן חשמל דירתי • מערכת חלוקה • רשת חשמל • מערכת תלת-פאזית | |
| בטיחות בחשמל | התחשמלות • לוח חשמל • קצר חשמלי • נתיך • הארקה • ממסר פחת • מפסק אוטומטי • צבע חוטי החשמל | |
| חוקים פיזיקליים | חוק קולון • חוק גאוס • חוק אוהם • חוקי קירכהוף • חוק שימור המטען החשמלי • חוק פאראדיי | |















