קריסה

ניסוי קריסה של עמודים הרתומים בצורות שונות

אורך הקריסה במוטות לפי צורת הריתום

קריסה היא כשל במבנה של הגוף כתוצאה מכוח לחיצה הפועל עליו. בעת תכן הנדסי בדיקה של תופעת הקריסה חשובה מכיוון שבחלק מהמקרים קריסה מתרחשת לפני תופעת הכניעה, שבה החומר עובר מהשלב האלסטי לשלב הפלסטי שלו (Pcr < σyp).

הכוח הגורם לקריסה קטן משמעותית מכוח הלחיצה שהיה גורם כשל לאלמנט של מבנה שאיננו גבוה. התופעה נקראת לפעמים גם אי יציבות אלסטית.

כוח הקריסה

כוח הקריסה, הכוח הקריטי הגורם לקריסת העמוד נתון על ידי הנוסחה שפותחה על ידי לאונרד אוילר במאה ה-18. הנוסחה מתאימה לעמוד אידאלי: ישר, הומוגני, ללא מאמץ התחלתי. נוסחת אוילר:

$F=\frac{\left(K \pi ^2 E I \right )}{l^2}$

או

$F=\frac{\left(\pi ^2 E I \right )}{(\mu l)^2}$

כאשר:

$F$ = הכוח הקריטי הוא כוח הלחיצה הצירי הגורם לקריסת העמוד

$E$ = מודול האלסטיות

$I$ = מומנט ההתמד של השטח

$l$ = אורך העמוד בין התמיכות

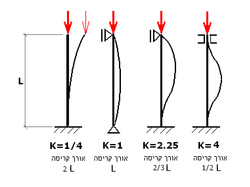
$\ K$ = מקדם המגדיר את אורך הקריסה והוא תלוי בצורת התמיכות של העמוד

• 1/4 - צד אחד רתום, צד שני חופשי לגמרי
• 1 - פרקים החופשיים להסתובב בשני צידי העמוד
• 2.05 - צד אחד רתום, צד שני פרק חופשי להסתובב
• 4 - שני הקצוות רתומים

$\ \mu$ = מקדם אורך הקריסה, אורך המוט הקורס כתלות בתמיכות

• 2 - צד אחד רתום, צד שני חופשי לגמרי
• 1 - פרקים החופשיים להסתובב בשני צידי העמוד
• ...0.699 - צד אחד רתום, צד שני פרק חופשי להסתובב
• 1/2 - שני הקצוות רתומים

הקריסה מושפעת מהגמישות של העמוד ולא מהחוזק של חומר העמוד.

הכוח הקריטי מושפע ישירות ממומנט האינרציה של השטח של העמוד.

תנאי הגבול - התמיכות משפיעות על אורך הקריסה וכך על כוח הקריסה.

מאמץ הקריסה

$\sigma = F/A = \frac{\pi^2 E}{(l/r)^2}$

כאשר:

• $\ F/A$ - מאמץ הקריסה: כוח הקריסה מחולק בשטח החתך של העמוד.
• $\ l/r$ - הגבהות של העמוד, מסומנת בדרך כלל על ידי האות: lambda - λ
• $\ r$ - רדיוס האינרציה של חתך העמוד
• $\ l$ - אורך הקריסה התלוי בצורת התמיכות

$\ \lambda = l/r$

צורות שונות של קריסה

• קריסה של מעטפת החומר כמו קריסה של מכל כתוצאה מתת לחץ.
• קריסה מקומית של חלק מבנה כמו קריסה של דופן קורה.
• קריסה תוך כדי פעולת פיתול.

קישורים חיצוניים

• קריסה, באנגלית
• מאמר בנושא קריסה, באנגלית
• קריסה באתר TWI, באנגלית
• דף חישוב מוט לקריסה, באנגלית
• קריסה דינמית, באנגלית

לקריאה נוספת

• Timoshenko S., Strength of Materials, 3rd edition, Krieger Publishing Company, 1976. ISBN 0882754203
• McGraw-Hill Encyclopedia of Engineering, Sybil P. Parker Editor in Chieh. McGraw Hill Book Company 1983, ISBN 0070454868
• Timoshenko & Gere, Theory of Elastic Stability, 2nd Ed. International Student Edition 1961