מעוות
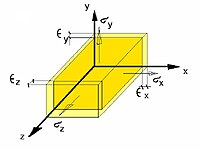

מַעֲוות הוא השינוי הגאומטרי החל בגוף הנתון תחת מאמץ. מעוות יכול להיות אחיד (הומוגני) בכל חלקי הגוף או בלתי אחיד. הביטוי הכללי למעוות הוא טנזור מעוות סימטרי. לרוב מתייחסים למעוות היחסי שהוא ערך חסר יחידת מידה המגדיר את השינוי ביחס לערך הראשוני לפני הפעלת המאמץ. בתחום האלסטי של החומר, הקשר בין המאמץ לבין המעוות נתון על ידי חוק הוק ומתואר באופן גרפי על ידי קו ישר. התחום הפלסטי של חומר מתאפיין בהשתנות שאינה ליניארית, ובמעוות שיורי שנותר לאחר הסרת העומס. דיאגרמת מאמץ - מעוות נותנת ערך נסיוני למעוות היחסי כתלות במאמץ הפועל על דגם של החומר הנבדק. המעוות היחסי מסומן באמצעות האות היוונית אפסילון ().
מעוות יחסי במוט[עריכת קוד מקור | עריכה]
כאשר המוט מתארך במאמץ מתיחה, הוא בעל ערך חיובי וכך גם המעוות היחסי . כאשר המוט מתקצר במאמץ לחיצה, בעל ערך שלילי וגם המעוות היחסי בעל ערך שלילי. האורך הראשוני של המוט הוא ערך חיובי.
המעוות היחסי כתוצאה ממאמץ הגורם לשינוי אורך של מוט נתון על ידי הביטוי:
כאשר
- - המעוות היחסי
- - האורך הראשוני של המוט
- - האורך הנוכחי של המוט
- - שינוי האורך של המוט
מעוות צירי ליניארי[עריכת קוד מקור | עריכה]
הביטוי למעוות היחסי בנקודה כלשהי בגוף מתקבל מהשינוי היחסי במרחק בין שתי נקודות:
כאשר:
- - המעוות היחסי
- - שינוי המרחק בין שתי נקודות קרובות
- - המרחק הנוכחי בין שתי נקודות קרובות לאחר הפעלת המאמץ
באופן כללי נגדיר את המעוות הליניארי בגוף על ידי שינוי המרחק בין שתי נקודות בגוף שנסמן אותן באופן אקראי על ידי A,B.
לשדה כלשהו של תזוזות המעוות הליניארי נתון על ידי הנגזרות החלקיות:
- ; ;
כאשר
- - מעוות בכיוון ציר "i"
- - הנגזרת החלקית של שדה התזוזות בנקודה כלשהי בכיוון ציר i
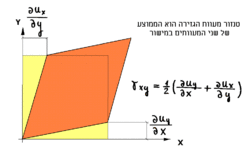
מעוות גזירה[עריכת קוד מקור | עריכה]

מעוות הגזירה מוגדר כשינוי הזוויתי בנקודה כלשהי בגוף בין שני קווים העוברים דרך הנקודה.
- ; ;
כאשר:
- - המעוות הזוויתי היחסי
מעוות נפחי[עריכת קוד מקור | עריכה]
המעוות הליניארי ומעוות הגזירה מגדירים באופן מלא את המעוות שעובר הגוף. ניתן להגדיר גם מעוות ניפחי
כאשר:
- - מעוות נפחי יחסי
- - הנפח ההתחלתי
- - הנפח הסופי לאחר הפעלת המאמץ
במערכת קואורדינטות ישרת זווית (קרטזית) המעוות הנפחי היחסי הוא בקרוב:
כאשר:
- - מעוות נפחי יחסי
- הם מעוותים יחסיים בכיוון הצירים x, y, z
טנזור מעוותים[עריכת קוד מקור | עריכה]
נבטא את המעוותים בצורה של טנזור:
בסימון של אינדקסים:
במערכת קואורדינטות ישרת זווית:
המעוות הנפחי הוא:
- gij
נכתוב טנזור מעוותים דו־ממדי:
המעוותים הראשיים
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Timoshenko S.P, Strength of Materials, 3rd edition, Krieger Publishing Company, 1976.
- Sybil P. Parker Editor in Chieh. McGraw-Hill Encyclopedia of Engineering, McGraw Hill Book Company 1983.
- S.P. Timoshenkoo & J.N. Goodier Theory of Elasticity, 3rd edition, International Student Edition, McGraw-Hill 1970.
- Shames I.H., Cozzarelli F.A., Elastic and inelastic stress analysis, Prentice-Hall, 1991.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מעוות גזירה, אוניברסיטת ויסקונסין-גרין ביי
- מעוות באי פאנדה
 עיוותים (מכניקה), דף שער בספרייה הלאומית
עיוותים (מכניקה), דף שער בספרייה הלאומית
| מאמץ (הנדסה) | ||
|---|---|---|
| מאמצים | מאמץ • מאמץ גזירה • מאמץ כפיפה • מאמץ לחיצה • מאמץ מתיחה • מאמץ פיתול • מאמץ קריסה • עייפות החומר | |
| נושאי עזר | מומנט כפיפה • מומנט כוח • אלסטיות • מעוות • חוק הוק • עקומת מאמץ-מעוות • כניעה (הנדסה) | |
| מודולי האלסטיות | מודול האלסטיות • מודול הגזירה • מקדם פואסון • קבועי לאמה • מודול הנפח | |
| שטחים ונפחים | שטח • מומנט התמד • מומנט ההתמד של השטח • מומנט התמד פולרי של השטח • משפט שטיינר-הויגנס • טנזור התמד • טבלת טנזורי התמד • מומנט ראשון של שטח | |
| נושאים משלימים | חוזק חומרים • טנזור מאמצים • מאמצים ראשיים • מעגל מור • היפותזות חוזק • שיטות אנרגיה • חוקי קסטיליאנו | |



























![{\displaystyle \varepsilon _{ij}=\left[{\begin{matrix}{\varepsilon _{x}}&{\frac {\gamma _{xy}}{2}}&{\frac {\gamma _{xz}}{2}}\\{\frac {\gamma _{yx}}{2}}&{\varepsilon _{y}}&{\frac {\gamma _{yz}}{2}}\\{\frac {\gamma _{zx}}{2}}&{\frac {\gamma _{zy}}{2}}&{\varepsilon _{z}}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0a60204abd75fed49d72261dc8cdddac1e66b9f)


![{\displaystyle \varepsilon _{ij}=\left[{\begin{matrix}{\varepsilon _{x}}&{\frac {\gamma _{xy}}{2}}\\{\frac {\gamma _{xy}}{2}}&{\varepsilon _{y}}\\\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdc5157d9b44190a41fea4250e5998e589452f08)


