ניתוח רשתות חברתיות
יש לערוך ערך זה. ייתכן שהערך סובל מבעיות ניסוח, סגנון טעון שיפור או צורך בהגהה, או שיש לעצב אותו, או מפגמים טכניים כגון מיעוט קישורים פנימיים.
| ||
| יש לערוך ערך זה. ייתכן שהערך סובל מבעיות ניסוח, סגנון טעון שיפור או צורך בהגהה, או שיש לעצב אותו, או מפגמים טכניים כגון מיעוט קישורים פנימיים. | |

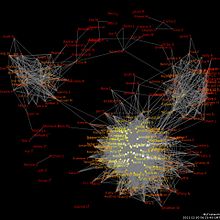
ניתוח רשתות חברתיות (באנגלית: SNA או Social Network Analysis) הוא גישה מדעית לחקר קשרים חברתיים, מרמת הפרט ועד מבנים חברתיים. בבסיסו של הניתוח הרשתי עומדת ההנחה שכדי להבין תופעה חברתית, לא מספיק לבחון את מאפייני האנשים היחידים הקשורים לתופעה, אלא יש לבחון את קשרי-הגומלין ביניהם במבנה החברתי. את הקשרים ניתן להציג בתרשים הנקרא 'סוציוגרם' בו הפרטים, השחקנים או הגורמים (נקרא גם: צמתים, ע"ע תורת הגרפים) מוצגים כנקודות, והקשרים (נקרא גם: קשתות) מוצגים כקווים. גישה זו משתמשת במושגים הלקוחים מתורת הגרפים המתמטית וממדע הרשתות.
מתוך ניתוח הקשרים בין הגורמים השונים ברשת, ניתן ללמוד על מרכזיותו של כל אחד מהם, על היררכיה בקבוצה, על הצפיפות של הקבוצה ועוד. חקר רשתות חברתיות נועד גם להבין תופעות שאינן נראות לעין ברמת היחיד ורק ניתוח רשתי של התופעה חושף אותה. למשל, מהו המרחק הממוצע, המינימלי או המקסימלי בין חברי רשת (באורכי קשת), מהו מבנה הרשת, לדוגמה רשת כוכב, רשת תאית, רשת שהתפלגות קשריה היא מסוג "זנב ארוך" למול רשת ממוצעית המתפלגת נורמלית ועד לרשת המתפלגת פואסונית וכו'.
ניתוח הרשת החברתית מאפשר ניתוח סטטי בודד (Snapshot) אך גם ניתוח דינמי של השתנות הרשת.
אחד מיתרונות השימוש בניתוח רשתות חברתיות הוא שהשיטה מאפשרת ביצוע מחקר על הרשת ומרכיביה, ללא הנחה מוקדמת לגבי אופי ומהות החברים בקבוצה, על ידי שימוש במדדי הרשת כגורם מכווין לשאילת השאלות.
למרות השוני הרב בין סוגי הקשרים החברתיים, מדע הרשתות מאפשר לזהות תופעות שפועלות בצורה זהה בכל רשת חברתית ובכל רשת "עולם אמיתי" באשר היא, כלומר, בכל רשת הקיימת בטבע.
מקובל לחלק בין ניתוח רשת חברתית כתחום חקר בסוציולוגיה ומדעי הניהול הנשען על מדדים סוציומטיים, לבין אנליזה מתמטית של רשת חברתית המהווה תחום חקר במתמטיקה, הנדסת תוכנה ומדעי הנתונים, הנשען על כלים מתמטיים וסטטיסטיים, החל מתורת הגרפים למידול בסיסי של רשת ועד ל-ERGM למידול אקספוננציאלי של רשת.
היסטוריה[עריכת קוד מקור | עריכה]
שורשיו התאורטיים של חקר הרשתות החברתיות מונחים בעבודתם של סוציולוגים מוקדמים כגון גאורג זימל ואמיל דורקהיים, שכתבו אודות החשיבות שבעיון בדפוסי יחסים שמחברים בין סוכנים חברתיים. מדעני חברה החלו להשתמש במושג "רשתות חברתיות" באיבה של המאה ה-20 כשכוונתם לכל מערכת יחסים מסובכת בין חברי מערכות חברתיות מכל קנה מידה שהוא, מהרמה הבין-אישית ועד לרמה הבין-לאומית. בשנות השלושים של המאה ה-20, יעקב מורנו והלן ג'נינגס הנהיגו לראשונה שיטות ניתוח רשתי בסיסיות. מורנו היה בין הראשונים להשתמש בסוציוגרם כשמיפה קשרי חברות בין תלמידים בבתי ספר יסודיים בארצות הברית. בשנת 1954 החל ג'ון ארונדל ברנס לעשות שימוש במושג דרך קבע כשם לדפוסי קשרים, כאשר הוא כולל בתוכו רעיונות שעד אז היו שכיחים הן בקרב הציבור והן בתחום מדעי החברה: קבוצות (דוגמת שבט או משפחה) וקטגוריות חברתיות (כמו מגדר ושיוך אתני). מלומדים וביניהם רונלד ברט, קתלין קארלי, מארק גרנובטר, דייוויד קראקהרדט, אדוארד Laumann, Anatol רפופורט, בארי ולמן, דאגלס ר לבן, הריסון לבן התרחב השימוש השיטתי רשת חברתית ניתוח. גם במחקר של ספרות, ניתוח רשת הוחל על ידי Anheier, Gerhards ורומו,[1] Wouter דה Nooy,[2] ו-Burgert Senekal.[3]
חלוצי המידול המתמטי של הרשתות היו פול ארדש ואלפרד רניי (במידול הרשת האקראית), ומנגד, חלוץ המחקר הסוציולוגי והסוציומטי ברשתות החברתיות (בהגדרת מדדי המרכזיות ברשתות) היה לינטון פרימן שנחשב למפתח מדדים רשתיים מרכזיים כדוגמת Betweenness Centrality, Freeman Centralization ועוד, תוך שבמאמרו המרכזי בתחום הראה שלא די בניתוח הפרטים ברשת על פי מס' הקשרים הישירים היוצאים מהם לשאר חברי הרשת, היות שבכל רשת חברתית ישנם לפחות שני אנשים עם אותו מס' קשרים (ובדרך כלל יש הרבה יותר בעלי מס' קשרים זהה) ולכן יש צורך להגדיר מדדי מרכזיות נוספים המביאים בחשבון גם את מיקום הפרט בתוך הרשת, קרבתו לפרטים אחרים (הנמדדת בסכימת המסלול הקצר ביותר לפרטים האחרים ברשת), מידת התיווך שלו (ברוקריות) וכו'. כמו כן Freeman היה הראשון שהגדיר, במאמרו המרכזי משנת 1977, את מדד צפיפות הרשת כיחס בין מס' הקשרים בפועל חלקי מס' הקשרים הפוטנציאלי האפשרי.
כניסת אתרי הרשתות החברתיות כדוגמת פייסבוק איפשרו לבצע ניתוח רשתות חברתיות על נתוני עתק (Big Data) של מיליוני צמתים וקשרים ברשת. התפתחות זו איפשרה הרחבה של תאוריות סוציולוגיות, פסיכולוגיות, סטטיסטיות והתנהגותיות לתחום העולם הדיגיטלי.
דוגמאות למחקרים מפורסמים בתחום חקר הרשתות החברתיות[עריכת קוד מקור | עריכה]
- הניסוי של סטנלי מילגרם על שש דרגות של הפרדה.
- "עוצמתם של קשרים חלשים" של הסוציולוג האמריקאי מארק גרנובטר.
- מחקרו של ויין זכארי על קשרים במועדון קראטה בשנות השבעים של המאה ה-20 שבמהלכו התפצל המועדון לשתי חבורות. זכארי עשה שימוש באלגוריתם זרימה מקסימלית - חתך מינימלי מתורת הגרפים כדי להדגים שניתן היה לבצע פרדקיציה על הפיצול.[4]
מדדים בניתוח רשתות חברתיות[עריכת קוד מקור | עריכה]
את המדדים ניתן לסווג למדדים ברמת הצמת/ים, מדדים ברמת הקשת/ות, מדדים ברמת הקבוצה/קהילה ומדדים ברמת הרשת כולה.
מדדי צמתים[עריכת קוד מקור | עריכה]
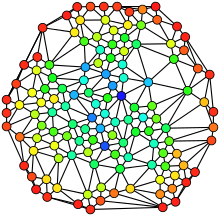
מרכזיות (אנ'): מכמתת את חשיבותו והשפעתו (במובנים שונים) של צומת מסוים או של קבוצה מסוימת בתוך רשת. המדדים הנפוצים לצומת בהם נעשה שימוש בניתוח רשתות חברתיות.[5]:
- דרגה או Degree - מספר הקשרים הנכנסים לצומת מתוך צמתים אחרים ברשת
- דרגה נכנסת (בגרף מכוון) - מספר הקשרים הנכנסים לצומת מתוך צמתים אחרים ברשת
- דרגה יוצאת (בגרף מכוון) - מספר הקשרים היוצאים מהצומת ומחברים אותו לצמתים אחרים ברשת
- דרגה ממושקלת (בגרף ממושקל) – סכום הקשרים של הדרגה היוצאת והנכנסת.
- Betweenness Centrality - מודד עד כמה צומת מסוים מקשר בין צמתים אחרים, שאילולא הוא היה מחבר אותן, צמתים אלו לא היו מקושרים זה עם זה. נמדד על ידי חישוב סך כל המסלולים הקצרים העוברים דרך הצומת ברשת.
בהקשר חברתי מדד זה יכונה "גשריות": גשר (Bridge (graph theory)): אדם אשר קשריו החלשים ממלאים חור מבני (Structural holes), ומספקים את הקשר היחידי בין שני פרטים או גושים. מושג זה כולל גם את המסלול הקצר ביותר כאשר המסלולים הארוכים מדי אינם יעילים כתוצאה מחשש לעיוות המסר או כשל במסירתו.[6]
- Closeness Centrality - מודד עד כמה צומת קרוב בממוצע לכל שאר הצמתים ברשת.,
- מדד וקטור עצמי (Eigenvector Centrality) - מודד עד כמה הצומת מקושר לצמתים אחרים בעלי דרגה גבוהה.
מדדי קשרים[עריכת קוד מקור | עריכה]
- כיוון הקשר
- קיימים קשרים חד כיווניים, שקיומם מצביע על קשר בין שחקן א' ל-ב' אך אינו מצביע בהכרח על קיום קשר בין ב' לא', ולעומתם קשרים דו כיווניים, המצביעים על הדדיות בין שני הצמתים. האם קשר הוא בעל כיוון, תלוי במציאות אותה ממדל הקשר. כמו כן לעיתים במציאות צומת יוכל ליצור קשר עם עצמו (Self loop) ולעיתים המציאות מחייבת שצומת אינו יכול ליצור קשר עם עצמו (לדוגמה דירוג במבחן סוציומטרי).
- סימן הקשר
- יש רשתות בהן בין השחקנים השונים מתקיימים יחסים חיובים ו/ או יחסים שלילים באותה העת. במצבים אלו חשוב לעשות הבחנה לגבי סימן הקשר האם הוא חיובי או שלילי (Friend או Foe). רשתות אלו נקראות רשתות מסומנות (Signed Graphs) ונעשה בהן שימוש להצגת מערכות יחסים שליליות וחיוביות באמצעות בחינת האיזון של המערכת.
ברשתות מסומנות, סימן חיובי מייצג קשר חיובי (ידידות, ברית, אהבה) ואילו סימן שלילי מייצג יחס שלילי (שנאה, יריבות, כעס). ניתן להשתמש בגרף מסומן כזה כדי לחזות מראש את התפתחות הרשת בעתיד. לפי תאוריית האיזון (Balance theory), מערכת מאוזנת מוגדרת כמעגל (מערכת שבה ניתן להגיע מכל צומת לעצמו בלי לחזור על קשתות) שבו מכפלת כלל הסימנים חיובית, ומערכת בלתי מאוזנת היא מעגל בו אותה מכפלה היא שלילית. לפי תאוריית האיזון, מערכת בלתי מאוזנת היא בעלת סבירות גבוהה יותר לשינוי דעתם של חלק מהחברים בה על חברים אחרים. לדוגמה, אם A ו-B מקיימים בניהם קשר חיובי ו-B ו-C גם הם מקיימים יחס חיובי, אבל C ו-A מקיימים יחס שלילי, קיים סבירות גבוהה שהמערכת תהפוך לבלתי יציבה, לדוגמה אם רק בין A ל-B ישנו יחס חיובי ואילו ל-A ול-B יחס שלילי ל-C. אם כן, ניתן להשתמש ברעיון של מערכות יציבות ובלתי-יציבות ככלי לניבוי עתידה של רשת.[7]
- חוזק הקשר
- נהוג להבחין בין קשרים חזקים ברשת לבין קשרים חלשים. קשרים חזקים משקפים מציאות בה בין שני צמתים מתקיימים יחסים קרובים או אינטנסיביים. קשרים חלשים הם קשרים בין שני צמתים המשקפים מציאות בה קשר בין שני אנשים הוא לא אינטנסיבי או במהותו אינו חזק.
בהקשר של מחקרים חברתיים, קשר חזק נקשר להומופיליה קרבה וטרנזיטיביות. קשר חלש נקשר עם גשרים. את עוצמת הקשר מבטאים על ידי מתן ציון מספרי לקשר. עוצמת הקשר ברשת יכולה להיות מנורמלת (בין 0 ל-1) או יכולה להופיע כעוצמה לא מנורמלת (המספר הממשי לדוגמה: כמות השיחות בין 2 אנשים בטלפון). מולטיפלקסיות: מספר האופנים שבהם מתקיים קשר. למשל, לזוג אנשים שקיימת ביניהם חברות ובנוסף לכך הם גם חולקים מקום עבודה משותף יש מולטיפלקסיות של 2. הוצעה תלות בין חוזק הקשר לבין מולטיפלקסיות שלו. הומופיליה: המידה שבה פרטים ייצרו קשרים עם הזולת אם הוא דומה להם, לעומת מצב שבו הוא שונה מהם. דמיון מוגדר כשוויון מגדר, גיל, עיסוק, סביבה חינוכית, מעמד, ערכים או כל מאפיין בולט אחר. סגירת משולשים (Triadic Closure): מדד של השלמות של שלישיות המקיימות ביניהם יחסים. ההנחה של פרט שקיימת בקבוצה בה הוא חבר מעגליות רשתית (כלומר, שחבריו מיודדים) נקראת טרנזיטיביות, והיא תוצר של הצורך של הפרט או המצב בסגירת-מעגל קוגניטיבית. קרבה (Propinquity) (אנ'): נטייה של פרטים ליותר קשרים עם פרטים אחרים שקרובים אליהם גאוגרפית.
מדדי רשת[עריכת קוד מקור | עריכה]
צפיפות (אנ'): היחס בין כמות הקשרים הישירים ברשת לבין המספר המרבי של קשרים אפשריים כאלה.[8][9] לדוגמה, אם ישנם 21 משתתפים, המספר הגבוה ביותר של קשרים פוטנציאליים למשתתף הוא 20. הצפיפות הגבוהה ביותר היא 100% (במקרה דנן 20/20); צפיפות של 5% משמעותה שקיים רק קשר אחד מתוך כלל הקשרים האפשריים (1/20).
מרחק: המספר המזערי ביותר של קשרים שנצרכים על מנת לחבר בין כל שני פרטים ברשת. כפי שהרעיון הופץ על ידי סטנלי מילגרם בניסוי העולם קטן ובמושג של שש דרגות של הפרדה.
חורים מבניים: חוסר בקשרים בין שני חלקים של רשת. זיהוי וניצול של חור כזה עשוי להעניק ליזם יתרון תחרותי. המושג הזה פותח על ידי רונלד בורט (Ronald Stuart Burt) ולפעמים הוא מוצג כתפישה אלטרנטיבית של הון חברתי.
- מדדים נאיביים כגון: מספר הצמתים, מספר הקשרים, מספר הקשרים ההדדיים, מספר הקשרים העצמיים (צומת מקושר לעצמו)
- מודולריות - מדד הבודק עד כמה הרשת ניתנת להגדרה על ידי קהילות.
- ניתן לעשות שימוש במדד הממוצע של הצמתים ברשת (למשל Betweenness ממוצע או Closeness ממוצע על פני כל הרשת וכדומה).
מדדי קבוצות וקהילות[עריכת קוד מקור | עריכה]
שימוש בניתוח רשתות חברתיות מאפשר לזהות 'מעגלים חברתיים' על בסיס הקשרים של הצמתים המייצגים את הפרטים בקבוצה ולזהות את מידת הליכוד שלה גוש מלוכד. קבוצה המגיעה ללכידות מקסימלית מוגדרת כ'קליקות' (Clique), כלומר, לכל פרט יש קשר ישיר לכל פרט אחר בקבוצה.
- לכידות
- המידה שבה פרטים מקושרים ישירות אחד למשנהו על ידי קשרים ליכודיים.
לכידות קבוצתית מתייחסת למספר המינימלי של צמתים שבהיעדרם תתפרק הקבוצה.[11] מדדים נוספים לקהילות:
- Reciprocity (הדדיות) - עד כמה הקשרים בין חברי הקהילה הם הדדיים,
- Density (צפיפות) - עד כמה מנוצל פוטנציאל הקשרים של כל חברי הקהילה לדבר עם כולם.
- ניתן לעשות שימוש במדד הממוצע של הצמתים בקהילה (למשל Betweenness ממוצע או Closeness ממוצע על פני כל הקהילה וכדומה).
ויזואליזציה של רשתות[עריכת קוד מקור | עריכה]
ייצוג ויזואלי של רשתות חברתיות הוא חשוב מפני שהוא מסייע להבין אינטואיטיבית את הנתונים שנאספו על אודות הרשת, וכן להנגישם בצורה נוחה למתבונן. מספר רב של שיטות וטכניקות להצגה ויזואלית של מידע שהושגה באמצעות ניתוח רשת הוצג לאורך השנים. תוכנות מחשב ניתוחיות מציעות כלים לוויזואליזציה כזו. הרשתות נחקרות על ידי פריסתן בדרכים שונות, ועל ידי הוספת ערכי צבע, גודל ותכונות מתקדמות אחרות לצמתים השונים. ייצוג ויזואלי של רשתות הוא אמנם כלי רב-עצמה ושימושי למי שמעוניין להציג מידע מורכב וסבוך, אבל יש לשים לב לכך שהצגת רשתות באמצעות ייצוג חזותי בלבד עלולה להוביל לחוסר דיוק או לפספוס של תכונות רשתיות שהיו נתפסות באמצעות ניתוח כמותי. תוכנות הוויזואליזציה המובילות הן NodeXL, Gephi, UciNet וכו'.
יישומים של ניתוח רשתות חברתיות[עריכת קוד מקור | עריכה]
חקר הרשתות החברתיות מנוצל ומצוי בטווח רחב של יישומים מעשיים, ודיסציפלינות. חלק מאותם יישומים כולל צירוף וכריית מידע, בניית מודלים להפצת רשתות, בניית מודלים של רשתות, ניתוח תכונות והתנהגויות של משתמשים, תמיכת משאבים בתחזוקת הקהילה, ניתוח של אינטראקציה מבוססת מיקום, שיתוף וסינון חברתיים, פיתוח מערכות המלצה וחיזוי קישורים ורזולוציית ישות. במגזר הפרטי, עסקים משתמשי בחקר רשתות חברתיות כדי לתמוך בפעילויות כגון ניתוח ואינטראקציה על הלקוח, ניתוח פיתוח מערכות מידע, שיווק וצרכי בינה עסקית. דוגמאות לשימושים במגזר הציבורי הן: פיתוח אסטרטגיות למחוברות מנהיגים, ניתוח של מחוברות ושל חשיפה למדיה של פרטים וקבוצות, ופתרון בעיות קהילתי. דוגמאות נוספות לשימוש בניתוח רשתות חברתיות: הפצת ממים, רשתות הכרויות, תרשימי שיתוף-פעולה (collaboration graphs), קרבה, העברת מחלות, התפשטות מחלות דרך מערכות יחסים מיניות.
לתחום יישומים בתחומים כגון: אנתרופולוגים, ביולוגים, דמוגרפים, חוקרי תקשורת, כלכלנים, גאוגרפים, היסטוריונים, מידענים, מדעי המדינה, פסיכולוגיה חברתית, מדעי ההתפתחות, בלשנים חברתיים, מדעי המחשב, זואולוגיה[12] ויישומים בהתמודדות עם הלבנת הון וטרור.[13] קיימים שימושים לחקר רשתות חברתיות גם בתחומי המודיעין, סיכול ריגול, אכיפת חוק וביטחון פנים. שימוש בטכניקה זו מאפשרת לחוקרים לזהות קבוצות חשאיות או סמויות, כגון רשת ריגול, משפחת פשע מאורגן או כנופיית רחוב. הסוכנות לביטחון לאומי בארצות הברית (NSA) משתמשת בתוכניות מעקב המוניות חשאיות במחשבים על מנת למצוא את המידע הדרוש לניתוח כזה על תאי טרור ועל קבוצות נוספות שנחשבות בעלות חשיבות לביטחון הלאומי. הסוכנות מגיע לעומק שלושה צמתים במהלך ניתוח זה. לאחר שהמיפוי הראשוני של הרשת מבוצע, נעשית אנליזה שמטרתה לקבוע את מבנה הרשת ולקבוע, למשל, מי הם המנהיגים. דבר זה מאפשר לצבא או לכוחות ביטחון פנים לכוון סיכולים ממוקדים שמטרתם לחסל או לשבות חברים בעלות ערך גבוה בתפקיד הנהגתי כשיטה להפריע לפעילות השוטפת של הארגון. הסוכנות התחילה לבצע גם ניתוח רשתות חברתיות על הקלטות של שיחות טלפוניות, המכונה מטא-דאטה, זמן מועט לאחר אירועי ספטמבר 11.[14][15]
תת-תחום של ניתוח רשתות חברתיות בנושא התנהגות ארגונית נקרא ניתוח רשתות ארגוניות (או: ONA - Organizational Network Analysis).
דוגמאות למחקרים[עריכת קוד מקור | עריכה]
- חקר מערכת הסחר הבינלאומית, כאשר הניתוח ישתמש במדינות כצמתים ברשת ובהיקפי סחר כקשרים. ניתוח כזה יכול להראות על גושים של מדינות ועל היררכיה בין הגושים ובתוכם.
- חקר רשתות של האקרים והבנת דפוסי ההתנהגות ואת הקשרים הנסתרים בין פרטים ומדינות בתחום זה.
- חקר קבוצת תמיכה - הצמתים יהיו החברים בקבוצה והקשרים יהיו בהתאם לתשובתם לשאלה 'ממי את/ה מקבל/ת ולמי את/ה מעניק/ה תמיכה בקבוצה'. רשת כזו יכולה לשמש לניתוח דפוסים של מתן תמיכה ויעילות של קבוצות תמיכה.
ייחוד שאלות מחקר רשתיות[עריכת קוד מקור | עריכה]
שאלות רשת בשונה מחקר גרפים, מוכוונות אל המציאות ממנה נובעת הרשת. שאלת רשת טובה עוזרת להבין טוב יותר את המציאות אותה היא ממדלת. ניתן לחלק את שאלות הרשת לשלוש רמות: הבנת הצמתים ברשת (מיקרו), הבנת הקהילות ברשת (מזו) והבנת הרשת כולה (מאקרו).
ברמת הצומת - לבד ממציאת הצמתים בולטים על פי הגדות מדדי הצמתים שונים, שאלת רשת היא שאלה אשר קושרת בין "תכונות" אובייקט כפי שהיא מתקיימות במציאות לבין התכונות הרשתיות של אותו אובייקט כאשר הוא ממודל כצומת ברשת שאנו מקימים. כאשר חוקרים קשרי חברות בחברה עסקית וממדלים את הקשרים הנירקמים בפינת הקפה במקום העבודה, שאלה רשתית ברמת הצומת תהיה "האם רוב העובדים אשר מתחילים את השיחות בפינת הקפה הם גברים או נשים" (העובדים יהיו הצמתים ברשת והקשרים בין הצמתים הם השיחות)? מבחינה רשתית מנסים למצוא שונות מובהקת בדרגה היוצאת של הנשים מול הגברים בחברה - בכל הנוגע לשיחות בפינת הקפה. השאלה אינה רק בונה את הרשת אלא שואלת עליה שאלה הלקוחה מתוך המציאות, שאלה המעניינת את החוקרים.
ברמת חקר הקהילות ברשת - לבד מזיהוי ומיפוי קהילות ומעקב אחר קשריהן הפנימיים והחיצוניים על פני זמן - שאלה רשתית שואפת לקשור בין זהות הקהילה (והחברים בקהילה) כפי שמצאו אלגוריתמים למציאת קהילות (כגון: ניומן, לוביין וליידן) לבין מכנה משותף "דמוגרפי" של חברי הקהילה שנמצאה.
ברמת חקר הרשת כולה - ניתן לחקור את השתנות הרשת ואת המדדים המרכזיים שאנו בוחרים לחקור בה (כגון Reciprocity, Density, Diameter) והשתנותם לאורך ציר הזמן. כמו כן ניתן להשוות בין שתי רשתות אשר נגזרות ממציאות דומה ולברר באמצעות ניתוח הרשת את המציאות. לדוגמה האם ה-Diameter של רשת הממדלת את קשרי החברות בשכבת גיל מסוימת בבית ספר משכבה סוציואקונומית גבוהה, גבוה בצורה מובהקת מה Diameter של רשת הממדלת את קשרי החברות בשכבת גיל מסוימת בבית ספר משכבה סוציואקונומית בינונית-נמוכה.
מציאת Data למחקר רשתי[עריכת קוד מקור | עריכה]
- כאשר רוצים לבחור בסיס נתונים למחקר רשתי יש להקפיד על מספר כללים בסיסים, המשמשים אותנו לבחינה האם Dataset מסוים מתאים לניתוח רשתי:
- בסיס הנתונים מורכב מאינטראקציות בין פריטים שונים, כאשר קיים ציון זמן (Time Stamp) לכל אינטראקציה..
- איתור של לפחות שתי ישויות בבסיס הנתונים המקיימות ביניהם יחס של רבים לרבים.
- איתור של תכונות (Features) של הישויות אותן רוצים למדל כ"צמתים" ברשת.
- איתור של תכונות (Features) של הקשר (Link) בין הישויות.
- להלן כמה קישורים נבחרים לאתרים בהם ניתן למצוא מאגרי נתונים רשתיים:
- https://www.aminer.org/data-sna
- https://snap.stanford.edu/data/
- https://kateto.net/2016/05/network-datasets/
יישומים בתחום החינוך[עריכת קוד מקור | עריכה]
בהקשר של למידה שיתופית נתמכת טכנולוגיה, חקר רשתות חברתיות הוא כלי עזר להבנת שיתוף הפעולה בין לומדים במונחים של כמות, תדירות ואורך-זמן, ובנוסף האיכות, הנושא ואסטרטגיות הקשר. יתר על כן, חקר רשתות חברתיות מסוגל להתמקד באספקטים מסוימים של חיבור הרשת, או על הרשת בכללותה. הוא משתמש בהצגה גרפית, מידע כתוב ובנתונים כדי לבחון את הקשרים בתוך רשת למידה שיתופית נתמכת טכנולוגיה (CSCL). בזמן יישום שיטות חקר רשתות חברתיות על CSCL, האינטראקציות בין המשתתפים נחשבות לרשת חברתית. הנושא בו הניתוח מתמקד הוא הקשרים שייצרו המשתתפים, כיצד הם תקשרו ולא כיצד כל משתתף התנהג בינו לבין עצמו. מספר מחקרים יישמו חקר רשתות חברתיות ב-למידה שיתופית נתמכת טכנולוגיה (CSCL) במגוון רחב של הקשרים. בין התוצאות, קורלציה בין נוכחות המורה לבין צפיפות הרשת, התייחסות רצינית יותר להמלצות של משתתפים ריכוזיים יותר, חוסר שכיחות של אינטראקציות בין בני מין שונה בתוך רשת, וכן תפקיד שולי יחסית שמשחק המורה ברשת למידה א-סינכרונית.[16] קיימים מספר מחקרים שעשו שילוב של אמצעי מחקר נוספים עם חקר רשתות חברתיות בבחינתם את הCSCL. ניתן להתייחס לזה כתהליך שיוביל לריבוי המהימנות של מחקרים אודות CSCL.
- שיטה איכותית - עקרונות חקר המקרה האיכותי יוצרות מסגרת מוצקה לאינטגרציה של חקר רשתות חברתיות בחקר חוויית CSCL.[17]
- מידע אתנוגרפי כגון ראיונות, שאלונים לחניך והשקפה בכיתה מצד שלישי לא משתתף.[18]
- מקרי בוחן: לבחון באופן מובן בין מצבי CSCL מסוימים ולקשר בין הממצאים לבין מגמות כלליות.
- ניתוח תוכן מציע מידע על אודות התוכן של ההתקשרות בין חברי הרשת.
- שיטה כמותית - שיטה זו כוללת ניתוחים סטטיסטיים פשוטים המתארים התרחשויות ומאפשרים לזהות את הגישה של חברים פרטיים בקבוצה שחקר רשתות חברתיות לא הצליח לעקוב אחריהם, כדי להתחקות אחרי נטיות כלליות.
- קובצי לוג אלקטרוניים מספקים מידע על השימוש שעושים הלומדים בכל שיתוף-פעולה.
- Multidimensional scaling - מנהל מעקב אחרי דמיון שקיים בין משתתפים, כך שיהיה ניתן להניח מידע דומה ביחד.
- תוכנות – QUEST, Nud*IST, SAMSA (System for Adjacency Matric and Sociogram-bases Analysis)
איסוף הנתונים לניתוח רשתות חברתיות[עריכת קוד מקור | עריכה]
קיימים מספר גישות לליקוט מידע ומיפוי רשתות בשיטות השתתפותיות, בייחוד כאשר השימוש בחקר רשתות חברתיות נעשה כדי להנחיל שינוי חברתי. בפרדיגמה זו, המשתתפים ממפים בעצמם את הרשתות על ידי רישום קשרים ידני (באמצעות עט ונייר או מחשב). דוגמה לשיטת עט ונייר לאיסוף מידע השתתפותי הוא, שמאפשרת גם איסוף נתונים לגבי תכונות הפרטים (השפעות ומטרות) היא שיטת Net-Map Toolbox. יתרונותיהן של שיטות מסוג זה הן היכולת של החוקרים לאסוף מידע איכותי ולא רק כמותי, וכן לתחקר את המשתתפים לצורך הבהרה.
פוטנציאל רישות חברתי[עריכת קוד מקור | עריכה]
פוטנציאל רישות חברתית הוא מקדם מספרי שניתן להגיע אליו באמצעות אלגוריתמים, כדי לייצג הן את הגודל של הרשת החברתית של פרט מסוים, והן את היכולת שלו להשפיע על הרשת. מילה נרדפת שקרובה במשמעותה, היא משתמש אלפא, אדם עם מקדם פוטנציאל רישות חברתית גבוה. קיימות שתי פונקציות עיקריות למקדמי פוטנציאל רישות חברתית:
- מיון וסיווג הפרטים בהתאם לפוטנציאל שלהם.
- שקילת הפרטים במחקרים שיווקיים.
על ידי חישוב הפוטנציאל של משיבים ושיווק ישירות לבעלי מקדם גבוה, החוזק והרלוונטיות של מחקר שיווקי שמשמש לשיווק ויראלי, מוגבר.
משתנים שמשמשים לחישוב מקדם הפוטנציאל כוללים בין היתר: השתתפות בפעילויות ברשת החברתית, חברות בקבוצות, תפקידי מנהיגות, זיהוי, הוצאה לאור\עריכה\תרומה למדיה שאינה אלקטרונית, הוצאה לאור\עריכה\תרומה למדיה אלקטרונית (אתרי מרשתת, בלוגים) ותדירות הפצת מידע בקרב הרשת בעבר. ראשי התיבות SNP) Social Networking Potential) וחלק מהאלגוריתמים הראשונים שנעשה בהם שימוש כדי לכמת את הפוטנציאל של פרט מסוים, תוארו במדריך "חקר הפרסום הולך ומשתנה". ע"ע שיווק ויראלי.[19] הספר הראשון שדן בשימוש המסחרי של משתמשי אלפא בקרב לקוחות טלקומוניקציה היה "3G Marketing" של אהונן, קאספר ומלקו ב-2004. הספר הראשון שדן במשתמשי אלפא באופן יותר נרחב בהקשר של שיווק חברתי היה Communities Dominate Brands (קהילות שולטות במותגים) של קהונן ומור ב-2005. ב-2012 ניקולא גרקו מהקולג' האוניברסיטאי של לונדון העביר שיחת TEDx (אנ') בנושא ההקבלה בין פוטנציאל הרשת החברתית לבין אנרגיה פוטנציאלית שמשתמשים יוצרים ושבה חברות צריכות לעשות שימוש. הוא טען ש-SNP הוא הנכס החדש שכל חברה צריכה לשאוף אליו כמטרה. [20]
ניתוח רשתות חברתיות בישראל[עריכת קוד מקור | עריכה]
המחקר בניתוח רשתות חברתיות במוסדות האקדמיים בישראל נחלק גם הוא למחקר מתמטי (הנשען על כלים מתמטיים וסטטיסטיים) ולמחקר סוציולוגי (העושה שימוש במדדים סוציומטיים), ובתפר ישנם מחקרים הנדסיים-ניהוליים בתחומים משיקים.
המחקר באנליזה מתמטית של רשתות חברתיות[עריכת קוד מקור | עריכה]
החוקרים המובילים במחקר המתמטי של ניתוח הרשת החברתית הם ד"ר מיכאל מן מרצה בפקולטה להנדסה באוניברסיטת תל אביב ומרצה חבר סגל בכיר באפקה במחלקה להנדסת תוכנה ומדעי המחשב וראש קבוצת המחקר של בית הספר להנדסת תוכנה, ופרופ' ברוך ברזל פרופ' במחלקה למתמטיקה באוניברסיטת בר-אילן (כתחום מחקר משני של מחקריו על דינמיקת רשתות מורכבות).
בד בבד עם התפתחותו ועליית קרנו של תחום מדע הנתונים, תחום האנליזה המתמטית של הרשתות (שעושה שימוש הן בכלים מתמטיים וסטטיסטיים, והן בכלים מתקדמים של כריית מידע) הולך וצובר תאוצה ככלי מרכזי לניתוח הרשתות החברתיות, ובמסלולי הלימוד להנדסה/מדעי הנתונים במרבית המוסדות האקדמיים למדעי הנתונים קורס רשתות חברתיות מוגדר כקורס ליבה.[21][22]
המחקר בניתוח סוציולוגי של רשתות חברתיות[עריכת קוד מקור | עריכה]
החוקרים המובילים במחקר הסוציולוגי של ניתוח הרשת החברתיות הם פרופ' שיזף רפאלי, בעבר ראש מרכז שגיא לחקר האינטרנט באוניברסיטת חיפה; וכיום נשיא מכללת שנקר; פרופ' דפנה רבן, מרצה בכירה בבית הספר לניהול והחוג לניהול מידע וידע באוניברסיטת חיפה; פרופ' אילן תלמוד, החוג לסוציולוגיה ואנתרופולוגיה באוניברסיטת חיפה, ד"ר עמית רכבי, הפקולטה לכלכלה ומנהל עסקים במרכז האקדמי רופין ועמית מחקר במרכז פדרמן לחקר הסייבר באוניברסיטה העברית, וד"ר אוסנת מוקרין, הפקולטה למדעי החברה, אוניברסיטת חיפה.
המחקר בניתוח הנדסי של רשתות חברתיות[עריכת קוד מקור | עריכה]
בין החוקרים המובילים בתחום המחקר ההנדסי-ניהולי ניתן לציין את פרופ' גלעד רביד מהמחלקה להנדסת תעשייה וניהול באוניברסיטת בן-גוריון, העוסק מחקרים בדינמיקת המסר של מרחבי אינטראקציה מקוונים, כריית מידע, ובמחקרים המקשרים תחומים של ממשקי אדם מחשב עם רשתות חברתיות (כגון גיימיפיקציה).[23]בנוסף בתחום ההנדסי ישנם מחקרים על אלגוריתמים יעילים לחישוב מדדי הרשתות במטריצת שכנויות, כדוגמת מחקריו של ד"ר מיכאל מן על אלגוריתמים למרכזיות במטריצת שכנויות וכן אלגוריתמים לחישוב Betweenness Centrality ברשת חברתית[24].
ראו גם[עריכת קוד מקור | עריכה]
- תורת הרשתות
- רשת חברתית
- דרגות ההשפעה ברשת
- אלברט-לסלו ברבאשי
- האתר של ברבאשי (עם וידאו מאמרים הרבה מידע)
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- נטפריקס - פודקאסט בנושא מדע הרשתות וניתוח רשתות חברתיות
- איתי להט ודן שוחט, כוחה הלא ייאמן של חברות, באתר כלכליסט, 25 במרץ 2010
- הרצאה של פרופ' רביד על הרשת
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Anheier, H.K.; Gerhards, J.; Romo, F.P. (1995). "Forms of capital and social structure of fields: examining Bourdieu's social topography". American Journal of Sociology. 100 (4): 859–903. doi:10.1086/230603.
- ^ De Nooy, W (2003). "Fields and networks: Correspondence analysis and social network analysis in the framework of Field Theory". Poetics. 31 (5–6): 305–27. doi:10.1016/s0304-422x(03)00035-4.
- ^ Senekal, B. A. 2012. Die Afrikaanse literêre sisteem: ʼn Eksperimentele benadering met behulp van Sosiale-netwerk-analise (SNA), LitNet Akademies 9(3)
- ^ ראו בויקיפדיה האנגלית, Zachary's karate club.
- ^ Opsahl, Tore; Agneessens, Filip; Skvoretz, John (2010). "Node centrality in weighted networks: Generalizing degree and shortest paths". Social Networks. 32 (3): 245–251. doi:10.1016/j.socnet.2010.03.006. אורכב מ-המקור ב-2018-02-26. נבדק ב-2018-03-23.
- ^ Granovetter, M. (1973). The strength of weak ties. American Journal of Sociology. Vol. 78. pp. 1360–1380. doi:10.1086/225469.
- ^ Cartwright, D.; Frank Harary (1956). "Structural balance: a generalization of Heider's theory" (PDF). Psychological Review. 63 (5): 277–293. doi:10.1037/h0046049. Link from en:Stanford University.
- ^ "Social Network Analysis". Field Manual 3-24: Counterinsurgency (PDF). Headquarters, Department of the Army. pp. B–11 – B–12.
- ^ Xu, Guandong; et al. (2010). Web Mining and Social Networking: Techniques and Applications. Springer. p. 25. ISBN 978-1-4419-7734-2.
- ^ Hanneman, Robert A.; Riddle, Mark (2011). "Concepts and Measures for Basic Network Analysis". The Sage Handbook of Social Network Analysis. SAGE. pp. 346–347. ISBN 978-1-84787-395-8.
- ^ Pattillo, Jeffrey; et al. (2011). "Clique relaxation models in social network analysis". In Thai, My T.; Pardalos, Panos M. (eds.). Handbook of Optimization in Complex Networks: Communication and Social Networks. Springer. p. 149. ISBN 978-1-4614-0856-7. מקדם התקבצות: מדד לסבירות ששני צמתים המקושרים לצומת מסוים יהיו מקושרים גם כן בין עצמם. מקדם גבוה יותר פירושו רמה יותר גבוהה של 'קליקיות'.[10]
- ^ קשר משפחתי, באתר קשר משפחתי, 2021-07-15
- ^ Ivaldi M.; Ferreri L.; Daolio F.; Giacobini M.; Tomassini M.; Rainoldi A. "We-Sport: from academy spin-off to data-base for complex network analysis; an innovative approach to a new technology". J Sports Med and Phys Fitnes. 51 (suppl. 1 to issue 3). The social network analysis was used to analyze properties of the network We-Sport.com allowing a deep interpretation and analysis of the level of aggregation phenomena in the specific context of sport and physical exercise.
- ^ "NSA Using Social Network Analysis". 12 במאי 2006. נבדק ב-19 ביולי 2013.
{{cite web}}: (עזרה) - ^ "NSA has massive database of Americans' phone calls". 11 במאי 2006. נבדק ב-19 ביולי 2013.
{{cite web}}: (עזרה) - ^ Aviv, R.; Erlich, Z.; Ravid, G.; Geva, A. (2003). "Network analysis of knowledge construction in asynchronous learning networks". Journal of Asynchronous Learning Networks. 7 (3).
- ^ Johnson, Karen E. (1996-01-01). "Review of The Art of Case Study Research". The Modern Language Journal. 80 (4): 556–557. doi:10.2307/329758. JSTOR 329758.
- ^ Martı́nez, A.; Dimitriadis, Y.; Rubia, B.; Gómez, E.; de la Fuente, P. (2003-12-01). "Combining qualitative evaluation and social network analysis for the study of classroom social interactions". Computers & Education. Documenting Collaborative Interactions: Issues and Approaches. 41 (4): 353–368. doi:10.1016/j.compedu.2003.06.001.
- ^ (Hrsg.), Sara Rosengren (2013). The Changing Roles of Advertising. Wiesbaden: Springer Fachmedien Wiesbaden GmbH. ISBN 9783658023645. נבדק ב-22 באוקטובר 2015.
{{cite book}}: (עזרה) - ^ "technology" "Watch "TEDxMilano - Nicola Greco - on math and social network" Video at TEDxTalks". TEDxTalks.
- ^ קורס ניתוח רשתות מורכבות כחלק ממסלול מדעי הנתונים במחלקה להנדסת תוכנה ומידע אוניברסיטת בן גוריון
- ^ לדוגמה קורס ניתוח רשתות חברתיות כקורס ליבה במסלול מדעי הנתונים באפקה
- ^ מאמר לדוגמה ברשתות חברתיות
- ^ ד"ר מיכאל מן (באתר המרצה בלשונית מחקר) בה מופיע בין תחומי המחקר של המרצה אלגוריתמים למציאת מרכזיות במטריצת שכנויות), באתר www.afeka.ac.il
