כוח קוריוליס


כוח קוֹרִיוֹלִיס, הנקרא גם אפקט קוריוליס, מתבטא בכך שביחס למערכת מסתובבת גופים סוטים מהתנועה בקו ישר, בהיעדר כוחות חיצוניים. הכוח נקרא על שם המדען הצרפתי גספאר קוריוליס, שתיאר אותו לראשונה ב-1835, אם כי כבר ב-1778 הוא הופיע בחישוביו של לפלס.
כדור הארץ מסתובב סביב צירו, ולכן כאשר מנתחים תנועה ביחס למערכת כדור הארץ, יש להתחשב באפקט קוריוליס. ההשפעה של אפקט קוריוליס גדלה ככל שהמהירות גדלה, או לחלופין, כאשר זמן התנועה מתארך. ולכן לכוח קוריוליס תפקיד חשוב במטאורולוגיה ובחישובים ארטילריים. בהסתמך על אפקט קוריוליס, הוכיח פוקו ב-1851 כי כדור הארץ מסתובב סביב צירו (ראו מטוטלת פוקו). טעות נפוצה מייחסת את כיוון הסיבוב של המערבולת שנוצרת בכיור כאשר המים יורדים לאפקט קוריוליס.
היסטוריה[עריכת קוד מקור | עריכה]


המדען האיטלקי ג'ובאני בטיסטה ריצ'ולי ועוזרו פרנצ'סקו מריה גרימלדי תיארו את האפקט בקשר לארטילריה בחיבורם "אלמגסט חדש" מ-1651 (שם המתייחס לספר אלמגסט, שנכתב במאה השנייה לספירה), בכותבם שסיבוב כדור הארץ אמור לגרום לפגז תותחים הנורה לכיוון צפון להיות מוסט מזרחה. ב-1674 קלוד פרנסואה מילייט דקלס תיאר בחיבורו "קורס במתמטיקה ארצית" כיצד סיבוב כדור הארץ אמור לגרום להסטה במסלולם של גופים נופלים וקליעים הנורים לכיוון אחד מהקטבים של כדור הארץ. ריצ'ולי, גרימלדי ודקלס תיארו את האפקט כחלק מטיעון נגד המערכת ההליוצנטרית של קופרניקוס. במילים אחרות, הם טענו שסיבוב כדור הארץ אמור ליצור את האפקט, כך שכישלון לזהות אותו מהווה עדות לנייחותו של כדור הארץ. משוואת התאוצה של קוריוליס נגזרה לראשונה על ידי אוילר ב-1749, והאפקט תואר גם במסגרת משוואות הגאות של פייר-סימון לפלס ב-1778. נקודת ציון נוספת היא האנליזה המתמטית של מסלולם של גופים המופלים ממגדל גבוה, שבוצעה על ידי קרל פרידריך גאוס ולפלס ב-1803. אחת התוצאות של הניתוח הזה היא חישוב תאורטי של הסטייה המזרחית של עצם המופל ממגדל בחצי הכדור הצפוני.
גספאר גוסטב קוריוליס פרסם מאמר ב-1835 על הנצילות האנרגטית של מכונות המכילות חלקים מסתובבים, כמו למשל גלגלי מים. המאמר התייחס לכוחות הנוספים שמורגשים במערכת ייחוס מסתובבת. קוריוליס חילק את הכוחות הללו לשתי קטגוריות. הקטגוריה השנייה הכילה כח תמכונתי למכפלה הווקטורית בין וקטור המהירות הזוויתית של מערכת קואורדינטות לוקטור מהירותו הקווית של החלקיק. קוריוליס התייחס לכוח הזה כאל "הכוח הצנטריפוגלי המורכב" באנלוגיה לכוח הצנטריפוגלי שמופיע בקטגוריה הראשונה. האפקט היה ידוע בתחילת המאה ה-20 כ"תאוצה של קוריוליס", ומ-1920 ואילך בשם "כוח קוריוליס".
ב-1856, ויליאם פרל הציע הסבר לתופעת הרוחות המערביות בקווי הרוחב 30-60 המבוסס על אפקט קוריוליס.
תיאור והגדרת כוח קוריוליס[עריכת קוד מקור | עריכה]
כוח קוריוליס הוא כוח מדומה, המופיע כיוון שמערכת ייחוס מסתובבת איננה אינרציאלית. בשונה מהכוח הצנטריפוגלי, שמופיע כל אימת שמערכת הקואורדינטות המקושרת למערכת הייחוס סובבת סביב ציר סיבוב, כוח קוריוליס מופיע רק כאשר מתווספת תנועה של העצם במערכת הקואורדינטות המסתובבת (לדוגמה, ילד שהולך על קרוסלה, תוך כדי שהיא מסתובבת), ועל כן התחשבות בו הכרחית לתיאור דינמיקה של עצמים במערכת מסתובבת. לעיתים, במצבים פיזיקליים מסוימים, נוח יותר להשתמש במערכת מסתובבת ולתאר את התנועה ביחס אליה. הכח מתכונתי למאסת הגוף, ולמכפלת מהירות הסיבוב ומהירות הגוף במערכת המסתובבת ומתואר בנוסחה:
כאשר מסת הגוף, וקטור המהירות שלו (במערכת המסתובבת), וקטור המהירות הזוויתית של המערכת, והמכפלה ביניהם היא מכפלה וקטורית.
הסבר אינטואיטיבי לכוח קוריוליס[עריכת קוד מקור | עריכה]
נניח שאנו עומדים על קרוסלה המסתובבת בקצב קבוע נגד כיוון השעון. על הקרוסלה מצויר קו ישר ממרכז הקרוסלה החוצה. אם נדמיין שאנו מנסים ללכת לאורך הקו, נגלה שעלינו להאיץ שמאלה על מנת להתאים את מהירותנו למהירות רצפת הקרוסלה (בין אם אנחנו הולכים לכיוון מרכז הקרוסלה או ממנו החוצה). כלומר נרגיש כאילו גופנו נמשך ימינה. משיכה זו היא כוח קוריוליס.

במילים אחרות, נניח שאנו עומדים מחוץ לקרוסלה ומסתכלים על גוף שנע לאורך הקו הישר ששרטטנו, ביחס לקרוסלה. כפי שהוסבר לעיל, הגוף חייב להאיץ שמאלה (מנקודת המבט שלנו, מבחוץ), ולכן חייב לפעול עליו כוח ממשי שמאלה (ר' תרשים). לעומת זאת, במערכת הייחוס של הקרוסלה, הגוף נמצא בשיווי משקל. נדמה שמופיע כוח המאזן את הכוח שמאלה. כוח מדומה זה, המכוון ימינה, הוא כוח קוריוליס.
נשים לב שהכוח ניצב למהירות, ופרופורציוני לה: ככל שנלך מהר יותר לאורך הקו, כך נצטרך להאיץ מהר יותר על מנת להתאים את עצמנו לרצפת הקרוסלה.
עד כה הסברנו מדוע כאשר מתקרבים אל מרכז הקרוסלה או מתרחקים ממנו, חווים כוח. אך מדוע אנו מצפים לחוות כוח כאשר אנו נעים סביב המרכז, מבלי להתקרב או להתרחק ממנו? ובכן, נמחק את הישר שעל רצפת הקרוסלה, ונצייר במקומו מעגל. נדמיין שאנו הולכים לאורכו במהירות קבועה. מצב זה שקול למצב שבו היינו שרויים במנוחה במערכת אחרת, שמסתובבת מהר יותר, או לאט יותר, בהתאם לאם אנו הולכים נגד כיוון השעון או עם כיוון השעון (נזכור שהקרוסלה מסתובבת נגד כיוון השעון). כלומר נצפה שהכוח הצנטריפוגלי שנחווה יגדל, או יקטן, בהתאמה. במילים אחרות, אם נחזור למערכת המקורית של הקרוסלה (זו שביחס אליה אנו נמצאים בתנועה) נצטרך להוסיף תיקון לכוח הצנטריפוגלי: כוח נוסף, שתמיד יהיה מכוון כלפי ימין (בין אם אנחנו נעים עם כיוון השעון או נגדו) - כוח קוריוליס.
תוכלו להראות, שאף על פי שההסבר לכוח נראה שונה למדי למקרה שאנו נעים על קו ישר או לאורכו של המעגל, גודלו של הכוח זהה, ונתון על ידי (ראו גם פסקה על "אפקט Eötvös" בהמשך הערך).
אם נמחק גם את המעגל ונתקדם בכיוון כלשהו, נוכל לפרק את התנועה לרכיב "בכיוון המרכז" (רכיב רדיאלי) ולרכיב "על המעגל" (רכיב משיקי). כיוון שהיחס בין הכוח למהירות שווה בשני המקרים, וכיוון שהכוחות שחישבנו קודם היו ניצבים לרכיבי המהירות המתאימים ומכוונים כלפי ימין, נקבל שסכום הכוחות יהיה ניצב לסכום המהירויות, וכיוונו - ימינה. קיבלנו בדיוק את כוח קוריוליס המתואר בפסקה הקודמת.
פיתוח מתמטי כללי, מקרים פרטיים[עריכת קוד מקור | עריכה]

הפיתוח משתמש בקשר בין הנגזרת של וקטור במערכת אינרציאלית לנגזרתו במערכת מסתובבת. עבור כל וקטור מתקיים השוויון:
.
כאשר הוא הנגזרת של במערכת האינרציאלית, ו הוא הנגזרת של במערכת המסתובבת במהירות זוויתית יחסית אליה. כלומר, מציגים את הווקטור במערכת הצירים המסתובבת וגוזרים אותו במערכת הצירים הזו, כך שהצירים עצמם אינם משתנים בזמן במערכת הייחוס הזאת.
בפרט, עבור התאוצה והמהירות, מתקיים:
,
אם נציב את הביטוי למהירות בביטוי של התאוצה, נקבל:
(השתמשנו בדיסטריביוטיביות של מכפלה וקטורית).
בהנחה ש קבוע (ולכן ) ניתן לפתוח את הנגזרת כך:
עתה נציב את הביטוי שקיבלנו, ונגיע ל:
.
כאשר היא תאוצת קוריוליס, ו היא התאוצה של הכוח הצנטריפוגלי, כוח מדומה נוסף במערכת.
(גודל ביטוי זה הוא ).
והכוח המדומה שיצפה במערכת המסתובבת הוא
.
האיבר הראשון בביטוי זה הוא כוח קוריוליס, והאיבר השני הוא הכוח הצנטריפוגלי. אם ניצב ל- אז הכוח הצנטריפוגלי הוא פשוט הביטוי המוכר:
קל לראות מהפיתוח שאם לא קבוע, כלומר (ישנה תאוצה זוויתית), הרי מלבד כוח קוריוליס והכוח הצנטריפוגלי יש להוסיף כוח מדומה נוסף השווה ל , אולם הפיתוח כולו מתבסס על ההנחה שציר הסיבוב הוא קבוע, ולכן הנוסחה נכונה רק אם משתנה רק בגודלו ולא בכיוונו משום שאז כל הפיתוח שגוי.
הסבר מתמטי פשוט למקרה של מהירות רדיאלית[עריכת קוד מקור | עריכה]
כוח קוריוליס מתקבל כאשר אדם הנמצא על שולי דיסקה מסתובבת מנסה לנוע במהירות קבועה בכיוון הרדיוס לכיוון מרכז המעגל. הכוח יופיע במאונך לכיוון ההתקדמות, במישור הדיסקה, מימין או משמאל (תלוי בכיוון סיבוב הדיסקה). לאדם על הדיסקה זהו כוח שאין לו הסבר ולכן נקרא "כוח מדומה", אולם לצופה מחוץ לדיסקה הכוח הוא כוח ממשי מאחר שהוא רואה שהמהירות המשיקית של האדם הנע על הדיסקה (לאורך הרדיוס) משתנה, ולכן מן ההכרח שפועל כוח שמקטין את המהירות המשיקית. זהו כוח קוריוליס.
חשוב להבין שמבחינת האדם על הדיסקה אין לו מהירות משיקית (מבחינתו אין סיבוב) אולם יש לו מהירות רדיאלית (מהירות בכיוון הרדיוס), אולם הצופה מבחוץ רואה גם את המהירות המשיקית וגם את המהירות הרדיאלית של האדם על הדיסקה.
ההוכחה שלהלן מתבצעת תוך התבוננות מחוץ לדיסקה:
תהי θ הזווית ברדיאנים, R רדיוס הדיסקה ו-S אורך קשת המעגל (המתאימה לזווית θ).
ידוע כי את אורך הקשת ניתן לתאר על ידי הנוסחה , ברור שלצופה מבחוץ גם R וגם θ הן פונקציות של t מאחר שהתנועת האדם על הדיסקה מתבצעת גם לאורך הרדיוס וגם בכיוון משיקי (מעצם סיבוב הדיסקה)
כדי למצוא את המהירות המשיקית נבצע גזירה לפי מכפלה (נשים לב , , מהירות זוויתית)
ולכן נקבל את המשוואה ( מהירות משיקית, מהירות רדיאלית, מהירות זוויתית)
כדי לקבל את התאוצה המשיקית (תאוצת קוריוליס) נגזור את המהירות המשיקית ונשים לב לכך ש וגם קבועים בזמן כלפי הצופה מחוץ לדיסקה.
ונקבל נסדר את המשוואה ונקבל (תאוצת קוריוליס)
ומכאן כוח קוריוליס
הערה: זהו תיאור סקלרי בלבד המתאר את גודל הכוח ולא את כיוונו.
הסבר מתמטי למקרה של מהירות משיקית - "אפקט אטווש"[עריכת קוד מקור | עריכה]
חשיבותו המעשית של "אפקט קוריוליס" נובעת בעיקרה על ידי רכיב התאוצה האופקית שלו הנגרמת על ידי תנועה אופקית.
ישנם רכיבים נוספים לכוח קוריוליס. גופים הנעים מערבה יוטו מטה (כלומר ירגישו כבדים יותר), בעוד גופים הנעים מזרחה יוטו מעלה (ירגישו קלים יותר). תוצא זה ידוע כ"אפקט אטווש" (Eötvös effect). רכיב זה של כוח קוריוליס הוא מרבי בקו המשווה. הכוח המופק על ידי אפקט זה הוא דומה לרכיב האופקי (כלומר מאותו סדר גודל), אבל הכוחות האנכיים החזקים בהרבה אודות לכבידה וללחצים שונים גורמים לרכיב זה להיות בלתי חשוב מבחינה דינמית.
בנוסף, גופים הנעים מעלה (כלומר החוצה מכדור הארץ) או מטה (אל מרכז כדור הארץ) יוטו מערבה או מזרחה בהתאמה. אפקט זה גם הוא מרבי בקו המשווה. מכיוון שתנועה אנכית בדרך כלל נמשכת משך זמן מוגבל, גודלו של אפקט זה מוגבל ומצריך מכשירי מדידה מדויקים כדי לגלותו. עם זאת, במקרה של שינויים גדולים בתנע, כמו במקרה של מעבורת חלל המשוגרת למסלול, האפקט הזה הופך למשמעותי. המסלול המהיר והחסכוני בדלק ביותר הוא שיגור מקו המשווה במסלול שמתעקל מזרחה.
דוגמה אינטואיטיבית[עריכת קוד מקור | עריכה]
נדמיין רכבת שנוסעת לאורך מסילה חסרת חיכוך הנמתחת לאורך קו המשווה. נניח גם, שכשהיא בתנועה, היא נוסעת במהירות מספיקה כדי להשלים הקפה מסביב לעולם ביום אחד (465 m/s). נתייחס לאפקט קוריוליס בשלושה מקרים: כאשר הרכבת נוסעת מערבה, כאשר היא במנוחה, וכאשר היא נוסעת מזרחה. בכל מקרה נתייחס תחילה למערכת הייחוס המסתובבת של כדור הארץ שבה פועל כוח קוריוליס, ולאחר מכן נבדוק גם במערכת ייחוס אינרציאלית, שבה לא פועלים כוחות מדומים. האנימציה ממחישה את שלושת המקרים כפי שהם נראים על ידי צופה במנוחה במערכת אינרציאלית הממוקם בנקודה קבועה מעל הקוטב הצפוני הנמצאת על ציר הסיבוב של כדור הארץ; הרכבת מסומנת באדום, והיא קבועה במקומה בהמחשה השמאלית, ונעה באחרות :

בשלושת המקרים כוח הכבידה המופעל על הרכבת זהה, אך המשקל שלה בפועל משתנה בין המקרים, כפי שנפרט להלן. המשקל בפועל בא לידי ביטוי בכוח שהרכבת תפעיל על המסילה, ולכן גם בכוח התגובה מהמסילה (כוח נורמלי). כמו כן, אם נוסעי הרכבת יעמדו על מכשיר למדידת משקל, המכשיר יראה מדידות שונות בכל אחד משלושת המקרים. את כל אחד מהמקרים ננתח גם ממערכת ייחוס מסתובבת וגם ממערכת ייחוס אינרציאלית, ונקבל בכל פעם שני הסברים שונים לאותה תוצאת משקל.
1. הרכבת נוסעת מערבה: במקרה זה, היא נעה נגד מגמת הסיבוב. לפיכך, במערכת הייחוס המסתובבת של כדור הארץ כוח קוריוליס מכוון פנימה לכיוון ציר הסיבוב של כדור הארץ (מטה) בעוצמה של כ-0.68% מכוח הכבידה. בנוסף, פועל במערכת יחוס זו כוח צנטרפוגלי בכיוון החוצה מציר הסיבוב (מעלה) בעוצמה של כ-0.34%. לכן סך כל הכוח המושך את הרכבת מטה גדול ב-0.34% מכוח הכבידה הרגיל. חלק מכוח זה יספק את הכוח הצנטריפטלי הדרוש לרכבת עבור תנועתה המעגלית, ורק החלק הנותר יהיה משקלה בפועל. הכוח הצנטריפטלי הדרוש שווה ל-0.34% מכוח הכבידה, ולכן בסופו של דבר משקלה בפועל יהיה זהה לכוח הכבידה.
- אם נסתכל על הרכבת הזאת במערכת הייחוס הלא מסתובבת של הצופה מעל הקוטב הצפוני, במהירות זו הרכבת נותרת נייחת כאשר כדור הארץ סובב מתחתיה. מכאן, הכוח היחידי הפועל עליה הוא הכבידה. מכיוון שבמערכת ייחוס זו אין כוחות מדומים, משקלה יהיה זהה בדיוק לכוח זה.
2. הרכבת במנוחה: מנקודת המבט של מערכת הייחוס הסובבת של כדור הארץ, מהירות הרכבת היא אפס, ולפיכך כוח קוריוליס הוא גם אפס. הכוח הצנטרפוגלי אינו תלוי במהירות הרכבת, ולכן הוא זהה למקרה הקודם, כלומר כוח בעוצמה של 0.34% מכוח הכבידה הפועל כלפי מעלה. לפיכך משקלה של הרכבת היה פחות 0.34% מכוח הכבידה, ולכן הרכבת ונוסעיה יהיו מעט קלים יותר מאשר במקרה הקודם.
- מנקודת המבט של הצופה מעל כדור הארץ, הרכבת כעת סובבת ביחד עם שאר כדור הארץ. 0.34% מכוח הכבידה מספק את הכוח הצנטריפטלי הדרוש כדי להשיג את התנועה המעגלית במערכת ייחוס זו. רק הכוח הנותר מהווה את משקלה בפועל, לכן שוב קיבלנו משקל הפחות ב-0.34% מכוח הכבידה.
3. הרכבת נוסעת מזרחה. במקרה זה, מכיוון שהיא נעה בכיוון הסיבוב של כדור הארץ, כוח קוריוליס יכוון החוצה מציר הסיבוב (מעלה) בעוצמה של 0.68% מכוח הכבידה. הכוח הצנטרפוגלי יוסיף עוד 0.34% כלפי מעלה, ועוד 0.34% מכוח הכבידה יושקעו בתאוצה הצנטריפטלית. לכן משקל הרכבת במקרה זה יהיה פחות ב-1.36% מכוח הכבידה הרגיל.
- ממערכת הייחוס האינרציאלית מעל הארץ, הרכבת נעה מזרחה במהירות כפולה מזו שהיא נעה במקרה 2. הכוח הצנטריפטלי גדל ביחס ריבועי למהירות, ולכן נדרש כוח גדול פי ארבעה יחסית למקרה הקודם, כלומר פי ארבעה מ-0.34%, שהם 1.36%. רק החלק הנותר של הכוח מהווה את משקלה, ולכן שוב קיבלנו שמשקלה יפחת ב-1.36%.
הוכחת שקילות האפקט בין שתי מערכות הייחוס[עריכת קוד מקור | עריכה]
הנוסחה להבדל בין משקלו של עצם כשהוא נע לעומת כשהוא נייח היא:
כאן,
- הוא התאוצה הרדיאלית המקזזת חלק מהמשקל
- היא מהירותו הזוויתית של כדור הארץ
- היא המהירות בכיוון מזרח-מערב
- הוא קו הרוחב שבו המדידות מבוצעות
- היא המהירות בכיוון צפון-דרום
- הוא רדיוס כדור הארץ
האיבר הראשון בנוסחה, , הוא האיבר המתאים לכוח קוריוליס ואפקט אטווש, בעוד שהאיבר השני הוא תיקון נוסף שאינו נובע מכוח קוריוליס אלא מעקמומיות כדור הארץ - העצם הנע נדרש לעקוב במסלולו אחר קרקע עקומה. בתנאים נורמליים (מהירויות נמוכות) האיבר השני קטן בהרבה מאפקט אטווש.
גזירת הנוסחה[עריכת קוד מקור | עריכה]
את הנוסחה ניתן לקבל מהנוסחה הבסיסית לכוח צנטריפטלי בתנועה מעגלית (הכבידה לא משתנה). התאוצה הצנטריפטלית הנדרשת מעצם כדי לנוע במסלול מעגלי ברדיוס R היא . עקב סיבוב כדור הארץ, לעצם נייח יש מהירות התחלתית בכיוון מזרח-מערב שגודלה . מהירותו הכוללת בכיוון מזרח-מערב היא לפיכך:
- . מהירותו בכיוון צפון-דרום היא פשוט . לפיכך ריבוע מהירותו הכוללת הוא (לפי משפט פיתגורס):
האיבר האחרון באגף ימין - - נכנס כבר "ממילא" לחישוב המשקל במקרה הנייח (כלומר הוא מקזז חלק ממשקל העצם כבר כשהוא במנוחה), ולפיכך הוא לא תורם כלום להבדל . לפיכך:
- .
עבודה[עריכת קוד מקור | עריכה]
כוח קוריוליס זהותית אינו מבצע עבודה. נזכיר כי הגדרת העבודה נתונה על ידי , כלומר, האינטגרל של המכפלה הסקלארית של הכוח הפועל על אלמנט של הדרך (המסלול), לאורך מסלול מסוים וקבוע . על ידי הצבת כוח קוריוליס נקבל כי עבודתו - . היות שהוקטור המתקבל מהמכפלה יהיה וקטור מאונך לוקטור (נובע מתכונות המכפלה הווקטורית) כשנכפול סקלרית את הווקטור החדש שמתקבל (שמאונך ל) באלמנט של הדרך (מכפלה סקלארית של שני וקטורים מאונכים), נקבל באופן זהותי, תוצאה שנובעת מתכונות המכפלה הסקלרית. כלומר, כוח קוריוליס אינו מבצע עבודה.
העובדה שכוח קוריוליס אינו מבצע עבודה מבדילה אותו מן הכוח הצנטריפוגלי, שמצביע תמיד רדיאלית החוצה ולפיכך מבצע עבודה במידה והעצם משנה את ריחוקו מציר הסיבוב, מה שמאפשר להגדיר מעין "פוטנציאל צנטריפוגלי" בעל סימטריה גלילית במערכת הייחוס המסתובבת. במבט ראשוני, "הפוטנציאל הצנטריפוגלי" עשוי להיראות כמו מושג מעורפל ואד-הוקי למדי, אולם חזרה למערכת הייחוס הלא מסתובבת מגלה מה מקורו - כתוצאה משינוי ריחוקו מציר הסיבוב, העצם מקטין או מגדיל את מומנט ההתמד שלו יחסית לציר זה, ומכיוון שהתנע הזוויתי שלו נשמר, האנרגיה הקינטית הסיבובית שלו חייבת להשתנות. ההבדל בין שתי האנרגיות הקינטיות הללו במערכת הלא-מסתובבת שווה במדויק לעבודת הכוח הצנטריפוגלי במערכת הייחוס המסתובבת.
הדגמה נאה לעקרון של הפוטנציאל הצנטריפוגלי היא העובדה שילד המתנדנד על נדנדה (שניתן למדלה כמטוטלת פיזיקלית) מסוגל לשנות את משרעת התנודה שלה גם ללא דחיפת הנדנדה על ידי גורם חיצוני - כל שעל הילד לעשות הוא להתרומם ולעמוד על מושב הנדנדה בזמן שהנדנדה במיקומה הנמוך ביותר (ומהירותה מרבית) ולשבת חזרה בעת שגובהה מקסימלי (ומהירותה אפס). כאשר הילד מגביה את מיקום מרכז מסתו, הוא מתאמץ להתרומם כנגד הכוח הצנטריפוגלי (והאנרגיה שהוא משקיע מגדילה את משרעת התנודה), בעוד שכאשר הוא מתיישב מהירות סיבוב הנדנדה היא אפס ולכן אין לכך השפעה על משרעת התנודה. מנקודת המבט של צופה חיצוני, כאשר הילד מתרומם, התנע הזוויתי הכולל של המערכת ילד + נדנדה נשמר, ולכן מהירות הנדנדה חייבת להשתנות (בדומה לרקדנית מסתחררת שמתמתחת וכך משנה את מהירות סיבובה).
שני עקרונות אלו, כלומר קיומו של פוטנציאל צנטריפוגלי ואי ביצוע עבודה על ידי כוח קוריוליס, עשויים לפשט מאוד בעיות הקשורות בתיאור התנועה (משוואת המסלול) של עצם לו מהירות התחלתית במערכת הייחוס המסתובבת: מן הפוטנציאל הצנטריפוגלי ניתן להסיק את ערכה המוחלט (גודלה) של המהירות כפונקציה של הרדיוס, בעוד שמכוח קוריוליס ניתן להסיק את עקמומיות המסלול הרגעית.
יישומים לתנועות על גבי כדור הארץ[עריכת קוד מקור | עריכה]

המושג "כוח קוריוליס" מתאים במיוחד לתיאור וניתוח תנועות אטמוספיריות (רוחות) על פני כדור הארץ. כדור הארץ (כמו כל הגופים השמימיים הסובבים סביב עצמם) לבש צורה של ספרואיד פחוס, באופן כזה שוקטורי השדה הכבידתי שהוא יוצר בכל נקודה על פניו מוטים במקצת ביחס לאנך המקומי לפני כדור הארץ, עם מגמת הטיה לכיוון הקטבים הגאוגרפיים. בעבור אלמנט מסה במנוחה על פני כדור הארץ, הרכיב האופקי של הכבידה מאזן במדויק את הרכיב האופקי של "הכוח הצנטריפוגלי" ובכך מונע מהמסה להחליק לעבר קו המשווה. כלומר, צורתו של כדור הארץ בשיווי משקל מעוצבת כך שמבין שני הכוחות המדומים החשובים, רק כוח קוריוליס רלוונטי לניתוח הנדידה האופקית של גושי אוויר.
כהערת אגב חשוב לציין, כי רעיון זה של מאזן בין הכוח הנורמלי, הצנטריפוגלי והגרביטציוני המכתיב את שיווי המשקל של גרמי שמיים, שימש למשל את ניוטון כשסיפק הערכה ראשונית למידת פחיסותו של כוכב כפונקציה של קצב הסיבוב שלו סביב צירו.
חשיבותו של כוח קוריוליס במטאורולוגיה[עריכת קוד מקור | עריכה]

אולי התוצא החשוב ביותר של אפקט קוריוליס הוא השפעתו על הדינמיקה בקנה מידה גדול של האוקיינוסים והאטמוספירה. במטאורולוגיה ואוקיינוגרפיה, נוח לתאר את הדברים ממערכת ייחוס מסתובבת שבה כדור הארץ נייח. לפיכך, יש להתחשב בכוח הצנטריפוגלי ובכוח קוריוליס. החשיבות היחסית של הכוחות האלה נקבעת על פי מספר רוסבי - פרמטר חסר ממדים המוגדר על ידי היחס בין האורך האופייני שבו השפעת כוח קוריוליס ניכרת לבין האורך האופייני של מערכת מזג האוויר. לסופות טורנדו יש מספר רוסבי גבוה, כך שבעוד שהכוחות הצנטריפוגליים המקושרים לטורנדו הם די משמעותיים, כוחות קוריוליס המקושרים לטורנדו נזנחים בחישובים.
מכיוון שזרמי ים בפני השטח של האוקיינוס מונעים על ידי תנועת הרוח מעל פני המים, כוח קוריוליס משפיע גם על התנועה של זרמי ים והוריקנים. רבים מהזרמים האוקיינים הגדולים ביותר סובבים סביב אזורים חמימים בעלי לחץ גבוה המכונים gyres. אף על פי שהסירקולציה של מי הים אינה משמעותית כמו זו של האוויר, ההסטה הנגרמת על ידי אפקט קוריוליס היא מה שיוצר את התבנית הספירלית של הזרימה באזורים הללו. במקרה האטמוספירי, התבנית הספירלית של הרוח היא מה שעוזר להוריקנים להיווצר - ככל שהכוח מאפקט קוריוליס חזק יותר, כך גם הרוח סובבת סביב מרכז הלחץ הנמוך ואוספת אנרגיה מהים מהר יותר, מה שמחזק את עוצמת ההוריקן.
האוויר במערכות לחץ-גבוה סובב במגמה כזאת שכוח קוריוליס מצביע רדיאלית פנימה, כשהוא כמעט מתאזן על ידי כוח גרדיאנט הלחץ המצביע החוצה. כתוצאה, האוויר סובב במגמת השעון מסביב לרמה ברומטרית בחצי הכדור הצפוני ונגד כיוון השעון בחצי הכדור הדרומי. אוויר מסביב לשקע ברומטרי סובב בכיוון ההפוך, כך שכוח קוריוליס מכוון רדיאלית החוצה וכמעט מאזן את גרדיאנט הלחץ המכוון פנימה.
זרימה מסביב לשקע ברומטרי[עריכת קוד מקור | עריכה]
אם שקע ברומטרי נוצר באטמוספירה, האוויר נוטה לזרום ישירות אליו, אבל מוטה בניצב למהירות שלו על ידי כוח קוריוליס. מערכת זרימה מעגלית בשיווי משקל מתהווה בדרך זו, שמכונה זרימה ציקלונית. מכיוון שמספר רוסבי נמוך, מאזן הכוחות הוא בעיקר בין כוח גרדיאנט הלחץ הפועל אל תוך השקע וכוח קוריוליס הפועל החוצה ממרכז הלחץ הנמוך.
במקום לזרום ישירות במורד הגרדיאנט, תנועות בקנה מידה גדול באטמוספירה והאוקיינוס נוטות להיות בניצב לגרדיאנט הלחץ. מצב כזה מכונה זרימה גיאוסטרופית. על כוכב לכת לא-מסתובב, זורמים היו זורמים לאורך הקו הישיר ביותר האפשרי, תוך שהם מעלימים במהירות הפרשי לחצים. המאזן הגיאוסטרופי הוא לפיכך שונה מאוד מהמקרה של "תנועות אינרציאליות" (ראו למטה).
מעגלים אינרציאליים[עריכת קוד מקור | עריכה]

גוש של אוויר או מים הנע במהירות ונתון רק להשפעת כוח קוריוליס ינוע במסלול מעגלי המכונה מעגל אינרציאלי. כיוון שהכוח תמיד מכוון בזוויות ישרות ביחס לתנועת הגוש, הגוש ינוע במהירות קבועה מסביב למעגל שרדיוסו ניתן בנוסחה:
כאשר היא תדירות קוריוליס (כאן הוא קו הרוחב). הזמן הלוקח לגוש להשלים סיבוב מלא הוא לפיכך . הערך האופייני של תדירות קוריוליס בקווי הרוחב הבינוניים הוא ; לפיכך בעבור מהירות רוח טיפוסית של 10 מטרים לשנייה הרדיוס יהיה 100 קילומטרים וזמן המחזור בערך 17 שעות. בעבור זרם ים במהירות אופיינית של 10 סנטימטרים לשנייה, רדיוס המעגל האינרציאלי יהיה קילומטר אחד.
על כוכב לכת מסתובב, משתנה עם קו הרוחב ועל כן מסלולי הגושים אינם מעגלים מושלמים. בפועל, כיוון שהפרמטר יחסי לסינוס קו הרוחב, רדיוס התנודות עבור מהירות ספציפית הוא קטן ביותר בקטבים (קו רוחב = ±90°) וגדל עם הקרבה לקו המשווה.
חוסר אחידותו של פרמטר קוריוליס גורמת למסלולי הגושים להיות פתוחים; כיוון שעקמומיות המסלול גדלה כשחבילת האוויר מצפינה וקטנה כשהיא מדרימה (זאת בחצי הכדור הצפוני), יתקבל מסלול אסימטרי ופתוח - עם כל סיבוב שהחבילה משלימה היא תסטה מעט צפונה. אפקט זה, המכונה סחיפת בטא (beta drift), הוא הסיבה לאחת התנועות העיקריות של סופה טרופית - תנועתה האיטית של הסופה לכיוון הקוטב הצפוני.
אפקטים ארציים אחרים[עריכת קוד מקור | עריכה]
אפקט קוריוליס משפיע במידה רבה על הסירקולציה האוקיינית והאטמוספירית בקנה מידה גדול, ומוביל להיווצרותם של דפוסים קבועים כמו זרם הסילון. דפוסים אלו נמצאים במאזן גיאוסטרופי, כלומר כוח קוריוליס וכוח גרדיאנט הלחץ הפועלים בהם מאזנים זה את זה. תאוצת קוריוליס אחראית גם להתקדמותם של סוגי גלים רבים באוקיינוסים ובאטמוספירה כגון גלי רוסבי וגלי קלווין. היא מרכזית גם בתיאור הדינמיקה של שכבת אקמן באוקיינוסים, ובביסוס המתמטי של תבנית הזרימה בקנה מידה גדול באוקיינוסים, הידועה כמאזן Sverdrup.
מסלולים בליסטיים[עריכת קוד מקור | עריכה]
אפקט קוריוליס הוא חשוב בבליסטיקה חיצונית לצורך חישוב מסלוליהם של פגזי ארטילריה ארוכת-טווח. הדוגמה ההיסטורית המפורסמת ביותר היא זו של תותח פריז, בו נעשה שימוש על ידי הגרמנים במהלך מלחמת העולם הראשונה כדי להפציץ את פריז ממרחק של בערך 120 קילומטרים. אפקט קוריוליס משנה במקצת גם את מסלולו של קליע, ומשפיע על הדיוק עבור מרחקי ירי ארוכים מאוד. שקלול אפקט קוריוליס לתיקון כיוון הירי נעשה בעזרת רובי צלפים מודרניים. בקו הרוחב של סקרמנטו ירייה ממרחק 1000 יארד תוסט ימינה בשיעור של 2.8 אינץ'. ישנו גם רכיב אנכי, כפי שהוסבר בחלק על "אפקט אטווש", שגורם ליריות מערבה לפגוע נמוך יותר, וליריות מזרחה לפגוע גבוה יותר.
נפילה חופשית של כדורים ממגדל גבוה[עריכת קוד מקור | עריכה]
מבחינה היסטורית, אחת החקירות האנליטיות הראשונות שזיהו במפורש איבר של כוח מדומה התלוי במהירות הגוף כפי שנצפית במערכת קואורדינטות מסתובבת (איבר קוריוליס) היא ניתוחם של גאוס ולפלס את מסלוליהם של גופים כבדים המופלים ממגדל גבוה (בהזנחת התנגדות האוויר). הניתוח שלהם היה מעמיק מאוד וכלל גם חישוב של איברים מסדרים גבוהים יותר (שלרוב הם זניחים), בנוסף על הסטייה המזרחית, שהיא הסדר הראשון בחישוב הסטייה. בפיתוח כאן נתייחס לסטייה המזרחית בלבד.
על גוף הנופל אנכית פועל רכיב אופקי של כוח קוריוליס המתכונתי למהירותו , למהירות הזוויתית של כדור הארץ, ולקוסינוס קו הרוחב בו הגוף נמצא. לפיכך, לאחר זמן נפילה , תאוצת קוריוליס מכוונת אופקית מזרחה וגודלה הוא:
- .
הסטייה המזרחית של מיקום פגיעת העצם בקרקע מתקבלת מאינטגרציה פעמיים של פונקציית התאוצה האופקית, כלומר:
אולם כאשר הוא גובה המגדל. לפיכך נקבל לבסוף: .
ויזואליזציה של כוח קוריוליס[עריכת קוד מקור | עריכה]


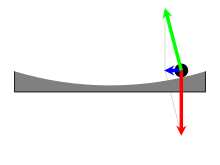
כדי להדגים את אפקט קוריוליס, ניתן להסתייע בהמחשה ויזואלית המיוחסת למטאורולוג אדולף שפרונג, שעושה שימוש בדיסקה קעורה בעלת צורה של פרבולואיד. על דיסקה שטוחה, האינרציה של הגוף המסתחרר יחד עמה גורמת לו ליפול מהקצה שלה. עם זאת, אם לדיסקה תהיה צורת הפרבולואיד הנכונה (המתאימה לתאוצת הכובד g ולקצב הסיבוב של הדיסקה), הרכיב של כוח הכובד המשיק לדיסקה הקעורה והכוח הצנטריפוגלי יאזנו זה את זה במדויק (ראו איור מימין), בדומה לכך שפני המים בדלי מסתובב מקבלים צורה פרבולואידית (ראו איור משמאל) כתוצאה מאיזון זה. משטח מלוטש כזה מאפשר לבודד את כוח קוריוליס.
דיסקות שטוחות הנחתכות מגלילים של קרח יבש ניתנות לשימוש לצורך המחשת האפקט, זאת שכן הן נעות כמעט ללא חיכוך על פני המשטח הפרבולי, מה שמאפשר להשפעה של אפקט קוריוליס על הדינמיקה שלהן להראות עצמה בבהירות מרבית. כדי לקבל תצוגה של התנועות כפי שנצפות ממערכת הייחוס המסתובבת של המשטח הפרבולי, מצלמת וידאו מותקנת על המשטח כך שהיא תסתובב יחד עמו, והתוצאות מוצגות באנימציה הימנית. באנימציה השמאלית, שמציגה את הדינמיקה מנקודת המבט של צופה נייח, הכוח הכבידתי במערכת האינרציאלית שמושך את הגוף למרכז (תחתית הדיסקה הקעורה) יחסי למרחק הגוף מהמרכז. כוח צנטריפטלי מהצורה הזאת גורם לתנועה אליפטית (זהו בעצם מתנד הרמוני דו-ממדי, ומכאן האליפטיות). באנימציה הימנית, שמראה את התרחיש מנקודת המבט של המערכת המסתובבת, כוח הכבידה המכוון רדיאלית פנימה (אותו הכוח כמו במערכת האינרציאלית) מאוזן על ידי הכוח הצנטריפוגלי החוצה (המורגש רק במערכת המסתובבת). כששני הכוחות הללו מבטלים זה את זה, במערכת המסתובבת הכוח היחידי שנצפה הוא כוח קוריוליס (שגם הוא מורגש רק במערכת הייחוס המסתובבת), והתנועה היא על כן בדיוק מעגל אינרציאלי! ניתוח או צפייה בתנועה המעגלית במערכת הייחוס המסתובבת היא פישוט בהשוואה לניתוח או תצפית של תנועה אליפטית במערכת האינרציאלית.
בגלל שהמערכת הזאת משלימה סיבוב מספר פעמים בדקה מאשר רק פעם אחת ביממה כמו כדור הארץ, תאוצת קוריוליס המופקת גדולה כמה מונים מזו הנגרמת מסיבוב כדור הארץ, ולפיכך היא גם קלה יותר להבחנה בקנה מידה מרחבי וזמני קטן.
כדור הארץ הוא אנלוגי לדיסקה פרבולית כזאת. כפי שהוסבר מקודם, סיבוב כדור הארץ גרם לו להתייצב בצורה ספרואידית כך שהכוח הנורמלי, כבידתו העצמית של כדור הארץ והכוח הצנטריפוגלי מאזנים זה את זה. בדומה לפני הקרקע של כדור הארץ, גם פני הים והאטמוספירה אנלוגיים לדיסקה פרבולית כזאת, וזאת גם הסיבה מדוע מושג המעגל האינרציאלי תקף גם עבור סירקולציות בים ובאטמוספירה, אם כי חוסר האחידות בפרמטר קוריוליס על פני כדור הארץ גורמת להן לא לאמץ תנועה מעגלית מושלמת.
אפקט קוריוליס הנגרם על ידי סיבוב כדור הארץ ניתן לצפייה באופן פחות ישיר דרך תנועת המשקולת של מטוטלת פוקו.
יישומים[עריכת קוד מקור | עריכה]
מד ספיקה קוריולי[עריכת קוד מקור | עריכה]

יישום טכנולוגי הרותם את אפקט קוריוליס לצרכים מעשיים הוא מד הספיקה הקוריולי (אנ'), מכשיר המודד את הספיקה של זורם הזורם דרך צינור. עקרון הפעולה של מכשירים כאלה הוא שימוש באקטואטור המייצר ויברציות מכניות סיבוביות בתדר גבוה של הצינור דרכו הזורם עובר. הויברציות, למרות שאינן לגמרי מעגליות, מספקות את מערכת הייחוס הסיבובית שמאפשרת לאפקט קוריוליס להתרחש. בזכות התדר הגבוה של הויברציות נוצרים כוחות קוריוליס חזקים על דפנות הצינור, מה שמייצר מעוותים קטנים בהן, שבאים לידי ביטוי בהפרשי מופע בתנודות בנקודות שונות בצינור. בעוד השיטות הספציפיות משתנות בהתאם לתכנון הספציפי של מד הספיקה, בכל התכנונים חיישנים מנטרים ומנתחים שינויים בתדר, הפרשי מופע, ואמפליטודות של הצינורות הרועדים. השינויים הנצפים מעידים על הספיקה המסית של הזורם.
מד הספיקה הקוריולי נחשב למכשיר מדידה מדויק ואמין ביותר משום שהוא מודד ספיקה מסית באופן ישיר ולא באופן עקיף כמו במדי ספיקה אחרים אשר פשוט דוגמים את מהירות הזורם בנקודה מסוימת. מדי ספיקה כאלו נתונים לשגיאות גדולות עקב חוסר האחידות של המהירות בחתך הצינור (בשל השפעות הצמיגות) וכן בשל תופעות טורבולנציה שונות שעשויות להתפתח במהירויות גבוהות. מד הספיקה הקוריולי, לעומת זאת, מודד את הספיקה בעזרת התנע הקווי הכולל של הזורם (כלומר מודד ערך ממוצע של מהירות הזרימה), אשר דרך אפקט קוריוליס מתורגם ללחץ הסטטי שמפעיל הזורם על דופן הצינור המתנודדת.
פיזיקה מולקולרית[עריכת קוד מקור | עריכה]
במולקולות רב-אטומיות, תנועת המולקולה ניתנת לתיאור כשילוב של סיבוב קשיח וויברציות פנימיות של האטומים מסביב לנקודות שיווי המשקל שלהם. כתוצאה מהויברציות של האטומים, האטומים הם בתנועה יחסית למערכת הקואורדינטות המסתובבת של המולקולה. אפקטי קוריוליס לפיכך נכנסים לתמונה, וגורמים לאטומים לנוע בניצב לכיוון התנודות המקורי שלהם. זה מוביל לערבוב בספקטרום המולקולרי בין רמות האנרגיה הסיבוביות והויברציוניות, שממנו קבועי צימוד קוריוליים ניתנים לחישוב.
מעוף חרקים[עריכת קוד מקור | עריכה]
זבובאים וכמה סוגים של עשים (פרפראים) מנצלים את אפקט קוריוליס במהלך מעופם בעזרת איברי חישה מיוחדים שממסרים מידע על המהירות הזוויתית של גופם.
כוחות קוריוליס הנגרמים על ידי תנועה קווית של איברי החישה במערכת הייחוס המסתובבת של גוף החרקים מזוהים על ידי איברים אלו. במקרה של זבובים, איברי החישה המיוחדים שלהם נקראים "בוכניות" והן מהוות מעין איברים דמויי משקולת הממוקמים בדיוק מאחורי הכנפיים שלהם.
בוכניות הזבוב תונדות במישור באותה התדירות כמו הכנפיים הראשיות כך שכל סיבוב של גוף הזבוב גורם לתנועה רוחבית שלהן ביחס למישור התנודה המקורי שלהן. הן במקרה של זבובים והן במקרה של עשים, אוסף של חיישנים מכניים בבסיס איברי החישה רגישים לשינויים בתדירות התנודה של הבוכניות, ובאמצעות מידע זה הזבוב מפרש את שינוי האוריינטציה שלו במרחב (שינוי זוויות הגוף).
יציבות נקודות לגראנז'[עריכת קוד מקור | עריכה]
באסטרונומיה, נקודות לגראנז' הן חמש נקודות במישור הסיבוב של שני גופים גדולים הסובבים אחד סביב השני, אשר עצם קטן המוצב בהן ומושפע רק מהכבידה של שני הגופים הללו יכול לשמור על מיקום קבוע ביחס לשני הגופים הללו. שלוש נקודות לגראנז' הראשונות (L1, L2, L3) מצויות על הישר שמחבר את שני הגופים הגדולים, בעוד ששתי נקודות לגראנז' האחרונות (L4 and L5) יוצרות (כל אחת בנפרד) משולש שווה-צלעות עם מיקומי כל אחד מהגופים הגדולים. נקודות L4 ו-L5, אף על פי שהן תואמות לנקודות מקסימום מקומי של הפוטנציאל האפקטיבי במערכת הייחוס המסתובבת ביחד עם הגופים הגדולים ("פוטנציאל אפקטיבי" זה נובע הן מכוחות הכבידה של שני הגופים הגדולים והן מן הכוח הצנטריפוגלי המקושר למערכת הדו-גופית המסתובבת), ולפיכך אינן מהוות נקודות שיווי משקל יציב, הן בכל זאת יציבות אודות לאפקט המשני של כוח קוריוליס, התלוי במהירות העצם ומעקם את מסלול העצם מסביב לנקודות אלו (במקום שינועו ישירות הרחק מנקודות אלו). מצב זה הוא בעל דמיון מסוים לעובדה המטאורולוגית שעל פני כוכב מסתובב, כיוון הרוחות מסביב לשקע או רמה ברומטרית הוא מסביב אליו, במקום לזרום ישירות אל תוכו/החוצה ממנו. יציבות זאת גוררת היתכנות של מסלולים קטנים מסביב ל-L4 או L5, הידועים גם דרך המונח tadpole orbits, ואכן ניתן למצוא אסטרואידים טרויאניים בנקודות L4 ו-L5 של מערכות דו-גופיות מסוימות.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- סרטון אנימציה המדגים את כוח קוריוליס.
- דיון באפקט קוריוליס הכולל ניתוח של מטוטלת פוקו וטורי טיילור (אנגלית)
- כוח קוריוליס - הפרכת מיתוסים (אנגלית)
- ארז גרטי, כוחות המעורבים בתנועה מעגלית, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 2 ביולי 2011
- כוחות מדומים במערכות מסתובבות, מתוך הבלוג "רשימות בפיזיקה עיונית".
- יונתן שנהב, על התנועות השונות של כדור הארץ, ומהו חוק קוריוליס?, באתר "הידען", 31 במרץ 2007
- science/Coriolis-effect כוח קוריוליס, באתר אנציקלופדיה בריטניקה (באנגלית)













































































