תורת הכאוס


תורת הכָּאוס (או התוהו) היא ענף במתמטיקה, בחיזוי מזג אוויר, בפיזיקה, בכלכלה ובפילוסופיה, המתארת מערכות רבות, שגם כאשר ידועים כל החוקים השולטים בהן, לא ניתן לחזות את התפתחותן לטווח ארוך. מערכות אלו מכונות מערכות דינמיות, והן בעלות רגישות גבוהה לשינויים מזעריים בתנאי ההתחלה. תופעה זו מכונה בלשון ציורית "אפקט הפרפר". דוגמאות למערכות כאלה הן האטמוספירה ומערכות כלכליות מסוימות.
החידוש הגדול בתורת הכאוס היה ההדגמה כי גם במערכות פשוטות ודטרמיניסטיות קיימים מצבים בהם התנהגות המערכת אינה ניתנת לחיזוי באופן אפקטיבי, משום שלשם כך יש צורך בידיעת התנאים ההתחלתיים בדיוק אינסופי - שאינו אפשרי.
בניגוד למה שהשם מרמז, "התנהגות כאוטית" אינה התנהגות שיש בה אי סדר מוחלט, אלא התנהגות חסומה; כלומר, מוגבלת לאירועים מסוימים, ושואפת למושך – אוסף יציב של מצבים. לפני פיתוחה של תורת הכאוס, המושכים היחידים הידועים היו ההתכנסות לנקודת איזון (אקוויליבריום), ההתכנסות למסלול מחזורי, וההתכנסות למסלול כמעט מחזורי. תורת הכאוס הוסיפה לרשימה מושך מוזר; מסלול שהמערכת מתכנסת אליו, בעל אופי פרקטלי.
מערכות בהן מתקיימת התנהגות כאוטית הן לא ליניאריות בהכרח. עבור משוואות הפרש, התנהגות כאוטית יכולה להופיע כבר במשוואה יחידה, כמו ההעתקה הלוגיסטית. עבור משוואות דיפרנציאליות רגילות, התנהגות כאוטית יכולה להופיע רק ממערכת בה לפחות שלוש משוואות אוטונומיות מסדר ראשון (כגון משוואות לורנץ), או מערכת של שתי משוואות עם תלות ישירה בזמן.
תיאור של התאוריה[עריכת קוד מקור | עריכה]
מערכת דינמית לא-ליניארית יכולה באופן כללי להתנהג באחד או יותר מהאופנים הבאים:
- להיות תמיד במנוחה
- לגדול באופן אינסופי (במערכות לא חסומות בלבד)
- להיות בתנועה מחזורית
- להיות בתנועה מחזורית-למחצה
- להיות בתנועה כאוטית
סוג ההתנהגות של המערכת תלוי במצב ההתחלתי שלה ובערכי הפרמטרים שלה. סוג ההתנהגות הקשה ביותר לחיזוי ולאפיון הוא הכאוטי, תנועה מורכבת לא-מחזורית שנתנה את שמה לתאוריית הכאוס.
תנועה כאוטית[עריכת קוד מקור | עריכה]
מערכת כאוטית מוגדרת כבעלת המאפיינים הבאים:
- תלות חזקה (אקספוננציאלית לרוב) בערך המדויק של תנאי ההתחלה.
- טרנזיטיביות מבחינה טופולוגית [דרושה הבהרה]
- המסלולים המחזוריים שלה צפופים במרחב המצבים [דרושה הבהרה]
הרגישות למצב ההתחלתי מתבטאת בכך שהבדל זעיר במצב ההתחלתי של שתי נקודות במערכת מוביל לשינוי משמעותי בהתנהגותן לאורך זמן. המערכות יתנהגו באופן זהה אם ורק אם התנאים המוקדמים שלהן זהים לחלוטין, דבר שאיננו ניתן ליישום. דוגמה לרגישות שכזו היא "אפקט הפרפר", המשמשת להמחשת הסיבה בגינה לא ניתן לחזות בדייקנות את מזג האוויר שיתקיים בעתיד הרחוק (מעבר לשבוע). אף על פי שתנועת כנפי הפרפר יוצרת שינויים זעירים באטמוספירה, די בהם על מנת ליצור שינוי משמעותי במזג האוויר עם חלוף הזמן. ההבדל העתידי בין המערכת נטולת-הפרפר והמערכת בעלת-הפרפר עשוי לגדול עד כדי כך, שכאשר באחת יתקיים יום שמש בהיר, בשנייה תתחולל סופת טורנדו. דוגמאות מוכרות אחרות לתנועה כאוטית הן הערבוב של צבעים נוזליים (חיתחות) ומערבולות אוויר.
מושכים[עריכת קוד מקור | עריכה]
ניתן לשרטט תנועה (כאוטית או שאיננה כאוטית) באמצעות דיאגרמת פאזה. כל אחד מצירי גרף הפונקציה מייצג ממד כלשהו של המצב, ללא ציר זמן. דוגמה: מיקום מטוטלת כנגד מהירותה; מטוטלת במנוחה תצויר כנקודה, בעוד שמטוטלת בתנועה מחזורית תצויר כעקומה סגורה פשוטה, הקרויה מסלול. המטוטלת עשויה לשרטט מספר אינסופי של מסלולים כאלה, הנבדלים זה מזה באנרגיה שלהם.
לעיתים קרובות, דיאגרמות פאזה מראות כי המצבים שמתוארים בהן מתקרבים בעקיבות לגבול מסוים. גם אם המסלולים שונים זה מזה בתכלית, כולם מסתיימים לבסוף באותה הנקודה. לכאורה, המערכת נמשכת אליה, ועל כן היא נקראת "המושך של המערכת". לדוגמה, מטוטלת אשר מאטה בהדרגה כתוצאה מחיכוך או מהתנגדות האוויר, תשרטט ספירלה המתכנסת אל נקודת האמצע, בה איבדה את כל האנרגיה שלה וחלדה מלנוע. נקודה זו, אליה תתכנס כל תנועת מטוטלת באשר היא, היא "המושך".
במערכות פשוטות לניתוח, המושך נקודתי לרוב, אך לא תמיד. מושכים אחרים עשויים לשרטט לולאות פשוטות (תנועה מחזורית); לולאות כפולות, בהן יותר משתי דרגות חופש (תנועה מחזורית-למחצה); ומבנים פרקטלים, המאפיינים "מושכים מוזרים" (תנועה כאוטית).
בכל נקודה של דיאגרמת הפאזה, המערכת תיטה להתפתח למצב שכן בצורה דטרמניסטית. אם המטוטלת שלנו נמצאת בנקודה מסוימת ויש לה מהירות מסוימת, ניתן לחשב את הנקודה הבאה ואת מהירותה. דיאגרמת הפאזה מייצגת שדה וקטורים, ועל כן ניתן להבין אותה באמצעות אנליזה וקטורית.
מושכים מוזרים[עריכת קוד מקור | עריכה]
תנועה כאוטית מתכנסת למושכים מוזרים, שהם בעלי מורכבות ופירוט אינסופיים. לדוגמה, מודל תלת־ממדי של מערכת מזג האוויר של לורנץ יוצר את "מושך לורנץ" המפורסם. הדיאגרמה של מושך זה היא אחת הדיאגרמות הידועות ביותר במערכות הכאוטיות, הן משום שהייתה מהראשונות שהתפרסמו, והן בשל צורתה האלגנטית, המזכירה כנפי פרפר.
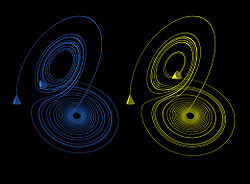
מושכים מוזרים קיימים במערכות דינמיות רציפות (כמו מערכת לורנץ) ובמערכות דיסקרטיות, בדידות (כמו מפת הנון). למערכות דינמיות דיסקרטיות אחרות יש מבנה דוחה שקרוי קבוצת ז'וליה, שנוצר בגבול בין אזורי משיכה בנקודות קבועות. אפשר לחשוב על קבוצת ז'וליה כ"דוחה מוזר". הן למושכים והן לדוחים המוזרים יש מבנה פרקטלי.
משפט פואנקרה-בנדיקסון מראה כי מושך מוזר יכול להיווצר במערכת דינאמית רציפה רק אם יש לו שלושה ממדים או יותר ("חוק השלוש" בא לידי ביטוי רבות בתורת הכאוס, גם במשוואות דינאמיות וגם במשוואות לוגיסטיות). עם זאת, מגבלה זו אינה קיימת במערכות דיסקרטיות, שמציגות מושכים מוזרים במערכות בעלות שני ממדים, ואפילו בממד אחד.
הדפוס של מערכת עם "מושך מוזר" הוא שונה. מערכות עם "מושכים מוזרים" מציגות התנהגות כאוטית. מיפוי המושך המוזר מראה, שהתנהגות המערכת בלתי צפויה, נראית "משונה" או "מוזרה", ואינה עקבית וסדירה כמו ה"מושך". מכיוון שהמערכת פתוחה לסביבה החיצונית שלה, היא מסוגלת להפגין גוונים רבים של תנועה. בכל אורגניזם בריא קיים "מושך מוזר", והוא עצמו "מושך מוזר" המתפתל, מתנועע, משתנה, רווי מעגלי משוב חיוביים הדוחפים את המערכת לכיוונים חדשים, ומעגלי משוב שליליים הדואגים לכך שהתהליך לא יגלוש לאקראיות צרופה, שתהרוס אותו.
היסטוריה[עריכת קוד מקור | עריכה]
שורשיה של תאוריית הכאוס בשנת 1900 לערך, במחקריו של אנרי פואנקרה על בעיית שלושת הגופים, העוסקת בתנועה של שלושה גופים בחלל, בהשפעת הכבידה. פואנקרה גילה שיכולים להתקיים מסלולים לא-מחזוריים, שאינם מתרחקים או מתקרבים לנקודה קבועה. מחקרים מאוחרים יותר, גם בנושא של משוואות דיפרנציאליות לא ליניאריות, נעשו על ידי ג'ורג' בירקהוף, אנדריי קולמוגורוב, מרי קרטרייט, ג'ון אדנזור ליטלווד וסטפן סמייל. מלבד סמייל (המתמטיקאי הטהור הראשון שחקר את הדינמיקה הא-ליניארית), העניקה הפיזיקה את ההשראה למחקר - בעיית שלושת הגופים במקרה של בירקהוף; מערבולות ובעיות אסטרונומיות במקרה של קולמוגורוב; והנדסת רדיו במקרה של קרטוויט וליטלווד. אף על פי שתנועה כאוטית של כוכבי-לכת טרם נצפתה, לא הייתה בנמצא תאוריה שיכלה להסביר את חוסר הסדר בתנועת נוזלים ואת השינוי הלא-מחזורי במעגלי רדיו.
תאוריית הכאוס תפסה תאוצה לאחר אמצע המאה העשרים, כאשר מדענים החלו להבין שתורת המערכות הליניאריות, התאוריה המערכתית המובילה באותו זמן, לא יכולה להסביר את התנהגותם של ניסויים מסוימים, כדוגמת ההעתקה הלוגיסטית. הזרז העיקרי להתפתחות של תאוריית הכאוס היה המחשב האלקטרוני, שכן פתרון בעיות מתמטיות בתאוריית הכאוס מצריך מספר אסטרונומי של חישובים, אותו לא ניתן לבצע ידנית בפרק זמן סביר. אחד המחשבים האלקטרוניים הראשונים, ה-ENIAC, שימש לעריכת מודלים פשוטים של מזג האוויר.
חלוץ מוקדם של התאוריה היה אדוארד לורנץ, שהתעניינותו בכאוס באה בדרך מקרה בזכות מחקריו על חיזוי מזג אוויר ב-1961. לורנץ השתמש במחשב בסיסי, עליו הריץ את הסימולציה האקלימית שלו. הוא רצה לחזור ולראות נתונים שראה קודם לכן, ובמטרה לחסוך זמן, הזין נתונים שהתקבלו באמצע סימולציה קודמת. להפתעתו, המחשב חזה כעת מזג אוויר שונה לחלוטין. לורנץ הבין שהשינוי נבע מכך שהזין נתונים החדשים בדרגת דיוק של שלוש ספרות אחרי הנקודה, ולעומת החישוב הקודם שנשען על דיוק של חמש ספרות אחרי הנקודה. כך נתגלה כי כל דרגת דיוק הנמוכה מאינסוף תוביל להעמקה בלתי נמנעת של ההבדלים בין שתי המערכות, עד לכדי כך שלא יהיה ביניהן עוד כל דמיון. גילוי זה סתר את הקונצנזוס השגוי שקדם לו, לפיו הבדל זעיר שכזה יהה זניח וחסר משמעות.
המונח כאוס במתמטיקה נטבע על ידי המתמטיקאי ג'יימס א. יורק. עם עליית כוח העיבוד של המחשבים בני זמננו, תאוריית הכאוס מהווה כיום תחום מחקר פעיל ביותר.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- ג'יימס גליק, כאוס, ספרית מעריב, 1991
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- יואב ויזל, ואולי בכל זאת יש סדר בטבע, מחשבות 68, ספטמבר 1996, עמ' 34–45
- תורת הכאוס, באתר אנציקלופדיה למתמטיקה (באנגלית)
- דוד גורביץ' ודן ערב, הערך "כאוס", באתר אנציקלופדיה של הרעיונות
- כאוס בפודקאסט המשחק הגדול (פרק להאזנה עם הטקסט)
- תורת הכאוס, באתר אנציקלופדיה בריטניקה (באנגלית)
 אסף רונאל, מחקר מציג פירוק מדויק של המערכת הכאוטית הראשונה שהתגלתה, באתר הארץ, 10 במרץ 2021
אסף רונאל, מחקר מציג פירוק מדויק של המערכת הכאוטית הראשונה שהתגלתה, באתר הארץ, 10 במרץ 2021- תורת הכאוס, באתר MathWorld (באנגלית)
 כאוס (פיזיקה), דף שער בספרייה הלאומית
כאוס (פיזיקה), דף שער בספרייה הלאומית
