זהות אוילר

באנליזה מתמטית, זהות אוילר, הקרויה על שמו של המתמטיקאי השווייצרי הידוע לאונרד אוילר, היא השוויון הבא:

$e^{i \pi} + 1 = 0 \,\!$

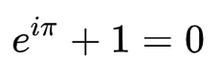
כל איברי הזהות הם מספרים קבועים:

• e הוא בסיס הלוגריתם הטבעי.
• π הוא היחס בין היקף המעגל לקוטרו.
• i הוא היחידה המדומה, מקיים: $i^2 = -1 \;\!$

יופי מתמטי

זהות אוילר נחשבת בעיני רבים כזהות יוצאת דופן בשל יופיה המתמטי. יופיה המתמטי נובע מהפעולות הבסיסיות שהיא משלבת בתוכה (חיבור, כפל והעלאה בחזקה) ומהקבועים המתמטיים הבסיסיים שהיא מקשרת ביניהם:

• e הוא מספר אי רציונלי (ואף טרנסצנדנטי) המופיע באינספור הקשרים שונים באנליזה מתמטית ותחומים משיקים. ספרתיו הראשונות הן 2.718281828.
• π הוא מספר אי רציונלי (ואף טרנסצנדנטי) המופיע גם הוא באינספור הקשרים בגאומטריה, אנליזה מתמטית ותחומים משיקים. ספרותיו הראשונות הן 3.1415926535.
• i הוא היחידה המדומה, הוא אחד משני השורשים הריבועיים של -1 (השני הוא -i).
• 1 הוא מספר טבעי המשמש כאיבר היחידה של כפל מספרים.
• 0 הוא מספר טבעי המשמש כאיבר האפס של חיבור מספרים.

עדות ליופי שרבים מייחסים לזהות ניתן לראות בכך שבמשאל קוראים שערך כתב העת "Physics World" בין קוראיו היא הגיעה למקום הראשון, יחד עם משוואות מקסוול.‏

הוכחה

ניתן להוכיח את הזהות על ידי הצבת $\ x=\pi$ בנוסחת אוילר:

$e^{i\pi} = \cos \pi + i\sin \pi$
$e^{i\pi} = 0 -1$
$e^{i\pi}+1=0$

כלומר, לאחר ההבנה כי הסינוס של פאי שווה לאפס, וכי הקוסינוס של פאי שווה למינוס אחת, מתקבלת זהות אוילר.

קישורים חיצוניים

• גדי אלכסנדרוביץ', נוסחת אוילר, ואיך היא קשורה למתנד הרמוני, באתר "לא מדויק"

הערות שוליים

ערך זה הוא קצרמר בנושא מתמטיקה. אתם מוזמנים לתרום לוויקיפדיה ולהרחיב אותו.