מכניקה של גוף קשיח

מכניקה של גוף קשיח (או של גוף צפיד) היא ענף פיזיקלי החוקר את תכונותיהם ותנועתם של גופים קשיחים. בהקשר זה, גוף קשיח (או: צפיד) הוא גוף אשר איננו משנה את צורתו במהלך התנועה או, במינוח מדויק יותר, זהו אוסף חלקיקים אשר המרחק בין כל שניים מהם נותר קבוע במהלך כל התנועה. מודל זה מוגבל לתיאור מצבים בהם ניתן להניח כי הגוף לא שינה את צורתו במהלך התנועה, או לחלופין, ששינוי הצורה של הגוף אינו משמעותי לניתוח התופעה.
ענף זה של המכניקה מטפל במספר תופעות הנוגעות לגופים קשיחים ובפרט מאפשר לנתח את תנועתם הסיבובית של גופים קשיחים סביב עצמם. הכלים של מכניקת הגוף הקשיח מאפשרים את ניתוחם ותכנונם של גופים כדוגמת הסביבון, הגירוסקופ ונדנדות למיניהן, כמו גם גלגלי שיניים ורכיבים מכניים נוספים.
הקשר לדינמיקה של חלקיק יחיד[עריכת קוד מקור | עריכה]

בדינמיקה הקלאסית של חלקיק יחיד (בהקשר זה הוא מכונה "גוף נקודתי"), על מנת לתאר תנועה של חלקיק במרחב נדרשים שלושה גדלים (לדוגמה: קואורדינטות האורך, הרוחב והגובה שלו), היות שהחלקיק יכול לנוע בשלושה כיוונים בלתי תלויים. במינוח פיזיקלי, לחלקיק יחיד יש 3 דרגות חופש מרחביות, והיות שהוא נקודתי אין לו דרגות חופש פנימיות. ניתן להראות כי לגוף קשיח, על אף שהוא עשוי להיות מורכב ממספר גדול מאוד של חלקיקים, יש תמיד בדיוק 6 דרגות חופש: תנועה בשלושה כיוונים, וסיבוב סביב שלושה צירים. בדומה לדינמיקה של חלקיק יחיד (ובאופן כללי יותר, בדומה לכל מערכת המילטונית עם מספר סופי של דרגות חופש), הדינמיקה של הגוף הקשיח מתארת את השינוי בזמן של שש הקואורדינטות של הגוף בכפוף לכוחות הפועלים עליו.
ניתן לפרק את תנועתו של גוף קשיח לתנועה קווית של מרכז המסה ולתנועה סיבובית של הגוף סביב עצמו. פירוק זה שימושי במיוחד, כיוון שתנועתו של מרכז המסה מתוארת לחלוטין על ידי הדינמיקה של חלקיק יחיד. באופן ציורי ניתן לומר כי מרכז המסה נע כאילו הוא היה חלקיק יחיד, והוא בכלל "לא יודע" שמחובר אליו גוף גדול. לעומת זאת, תנועתו הסיבובית של הגוף סביב עצמו היא מסובכת יותר ודורשת כלים מתמטיים מורכבים יותר כדי לנתחה.
הגדלים היסודיים[עריכת קוד מקור | עריכה]
בניתוח דינמיקה של חלקיק יחיד נהוג להגדיר מספר גדלים: מהירות, תנע, אנרגיה, וכיוצא בהם. עבור תנועה סיבובית של גוף קשיח, ניתן להגדיר גדלים דומים:
- התנע הקווי של גוף נקודתי מוגדר כמכפלת מהירותו של הגוף במסתו, או בניסוח מתמטי: . ההיטל של וקטור התנע על ציר מסוים מהווה, באופן אינטואיטיבי, מדד ל"כמות התנועה" בציר זה. באופן דומה, מוגדר וקטור התנע הזוויתי, , כך שההיטל שלו על ציר מסוים מהווה מדד ל"כמות הסיבוב" סביב ציר זה. התנע הזוויתי מוגדר כמכפלה וקטורית של מיקום הגוף בתנעו הקווי, או בכתיב מתמטי: . הבדל משמעותי בין התנע הקווי לתנע הזוויתי הוא שהתנע הקווי מקביל למהירות, ואילו וקטור התנע הזוויתי ניצב למישור הסיבוב של הגוף. ניתן גם להציג את התנע הזוויתי על ידי מכפלת מומנט ההתמד שלו במהירותו הזוויתית (ראו הסבר בהמשך).
- החוק השני של ניוטון קובע כי נגזרתו של התנע הקווי לפי הזמן היא גודל הכוח הפועל הגוף, או בשפה מתמטית: . בצורה פשטנית, ניתן לומר שגודל זה גורם לשינוי בתנועה הקווית. המקביל הסיבובי אליו, הגורם כביכול לשינוי בתנועה הסיבובית של הגוף הקשיח, נקרא מומנט כוח, , והוא מוגדר כמכפלה ווקטורית בין הכוח למיקומו של הגוף. בשפה מתמטית: . הכללה ישירה של החוק השני של ניוטון קובעת כי . כלומר, בהיעדר מומנטים חיצוניים, התנע הזוויתי במערכת נשמר.
- בדינמיקת החלקיק, מהווה המסה מדד להתנגדותו של גוף לשינוי תנועתו הקווית. הגודל המקביל בדינמיקה של גוף קשיח נקרא מומנט התמד, המבטא מדד להתנגדותו של גוף לשינוי בתנועה הסיבובית שלו. היות שניתן לסובב גוף במספר כיוונים, מומנט ההתמד לא יכול להיות מורכב ממספר אחד בלבד (כמו המסה) אלא צריך להכיל מידע על התנגדות הגוף לסיבוב בכל הכיוונים. בשפה פיזיקלית אומרים כי מומנט ההתמד הוא טנזור (בניגוד למסה שהיא סקלר). עם זאת, בבעיות פשוטות שבהן הגוף מסתובב תמיד סביב ציר אחד (כמו במקרה של קרוסלה, לדוגמה) ניתן להחליף את הטנזור המלא של מומנט ההתמד במספר יחיד. קל לייצג את טנזור מומנט ההתמד על ידי מטריצה, ובכל פעם ש־ מופיע במשוואה, יש להבין את המשוואה כמכפלה של מטריצה בוקטור. כאשר רוצים להדגיש את עובדת היותו טנזור, הוא מסומן עם גג: . לדוגמה, הנוסחה מבטאת את העובדה שישנם מצבים בהם התנע הזוויתי אינו מקביל למהירות הזוויתית.
להלן טבלה המדגימה את הגדלים המקבילים בתיאור תנועתו הקווית והסיבובית של הגוף:
| תנועה קווית של גוף נקודתי | תנועה סיבובית של גוף קשיח | ||
|---|---|---|---|
| תנע קווי | תנע זוויתי | ||
| כוח | מומנט הכוח | ||
| מסה | מומנט ההתמד | ||
| העתק קווי | זווית הסיבוב | ||
| מהירות קווית | מהירות זוויתית | ||
| תאוצה קווית | תאוצה זוויתית | ||
| החוק השני של ניוטון | |||
| אנרגיה קינטית קווית | אנרגיה קינטית זוויתית | ||
תוצאות חשובות של התורה[עריכת קוד מקור | עריכה]
בתורת הגוף הקשיח ישנן מספר תוצאות חשובות הנוגעות לתנועתם של גופים קשיחים. תובא כאן סקירה של מספר נקודות מרכזיות.

חישוב מומנט ההתמד[עריכת קוד מקור | עריכה]
 ערכים מורחבים – מומנט התמד, משפט שטיינר
ערכים מורחבים – מומנט התמד, משפט שטיינר
מומנט ההתמד סביב ציר מסוים מוגדר כסיכום התרומות של כל אחת מהמסות המרכיבות את הגוף למומנט הכללי:
כאשר הוא המרחק של המסה ה־i מציר הסיבוב. בגבול הרצף, הסכום הופך לאינטגרל:
וכאן הוא המרחק של המסה m מציר הסיבוב.
כתוצאה מהגדרה זו, מתקבלת דרך לחשב את מומנט ההתמד של גוף סביב ציר תנועה מסוים, בהינתן מומנט ההתמד של הגוף סביב ציר מקביל, העובר דרך מרכז המסה של הגוף. תוצאה זו נקראת "משפט שטיינר". בניסוח מתמטי, אם הוא מומנט ההתמד סביב ציר העובר במרכז המסה, אז , מומנט ההתמד סביב ציר אחר המקביל לו נתון בנוסחה , כאשר m היא מסת הגוף ו־d המרחק בין שני הצירים.
טנזור מומנט ההתמד[עריכת קוד מקור | עריכה]
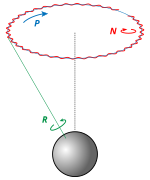
כיוון שטנזור ההתמד סימטרי, ניתן ללכסן אותו עבור כל גוף קשיח. בצורתו המלוכסנת של הטנזור, הצירים המתאימים לרכיביו נקראים "צירי התנועה הראשיים" (או, "צירי התנועה הטבעיים") והערכים על האלכסון הם מומנטי ההתמד הראשיים. לצירים הראשיים של גוף יש חשיבות רבה, כיוון שכאשר גוף מסתובב סביב ציר ראשי שלו, ציר הסיבוב נשאר קבוע. כלומר, לא מתרחשת נקיפה. תוצאה חשובה זו מראה שלכל גוף קשיח קיימים שלושה צירים (לפחות) שסביבם ניתן לסובב את הגוף וציר הסיבוב יישאר קבוע. פרט לחשיבות התאורטית של התופעה, יש לה גם שימוש מעשי חשוב: בעת איזון גלגל כלי רכב במוסך, פעולות המכונאי מכוונות לכך שציר הסיבוב הראשי של הגלגל יהיה מקביל לסרן המכונית, שאם לא כן, הגלגל "ירצה" לשנות את ציר הסיבוב שלו, מה שיגרום להפעלת כוח על הסרן ויכול אף להביא לשבירתו.
מבחינת החישוב, חלק מהמשוואות הופכות פשוטות יותר אם מלכסנים את טנזור מומנט ההתמד. כך, למשל, האנרגיה הקינטית הכוללת במצב זה היא סכום האנרגיות המתקבלות מתנועה סביב כל אחד מהצירים.[1]
המשוואות המתארות תנועות מורכבות של גוף קשיח, בפרט כאלו הכוללות נקיפה ונוטציה, נקראות משוואות אוילר, על שמו של הפיזיקאי והמתמטיקאי לאונרד אוילר. אלו הן שלוש משוואות הקושרות את מומנטי ההתמד של הגוף סביב ציריו הראשיים, מומנטי הכוח הפועלים עליו, המהירויות הזוויתיות סביב צירים אלו וקצב השינוי שלהן (התאוצה הזוויתית) במערכת הייחוס של הגוף הנע.[2]
גוף קשיח בתורת היחסות[עריכת קוד מקור | עריכה]
תורת היחסות שוללת את קיומם של גופים קשיחים, שכן כאשר מתחיל לפעול כוח על גוף לא ייתכן שכל חלקיו יתחילו לנוע באופן מיידי, בגלל המגבלה של העברת האינפורמציה (קרי – תגובת חלקיו הרחוקים ביחס לנקודת הפעלת הכוח) במהירות הנמוכה ממהירות האור. לכן, אין טעם לדבר על מכניקה יחסותית של גוף קשיח במובן הפשוט. עם זאת, למושגים כמו תנע זוויתי יש חשיבות רבה בתורת היחסות, נזכיר כי תנע זוויתי איננו בהכרח קשור לגוף קשיח.
מקורות[עריכת קוד מקור | עריכה]
- Kittel, Mechanics, Berkeley Physics Course
- L. D. Landau and E. M. Lifshitz, Mechanics, Course of Theoretical Physics, 3rd ed., Vol. 1.
- Michael Gedalin,Rigid body rotation I, Theory(הקישור אינו פעיל),Rigid body rotation II, Applications(הקישור אינו פעיל)
ראו גם[עריכת קוד מקור | עריכה]
|
עיינו גם בפורטל פורטל הפיזיקה מהווה שער לחובבי הפיזיקה ולמתעניינים בתחום. בין היתר, בפורטל תוכלו למצוא מידע על פיזיקאים חשובים, על ענפי הפיזיקה ועל תאוריות פיזיקליות. |
תחומים קרובים
בפיזיקה ובמתמטיקה
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ בכתיב מתמטי: .
- ^ המשוואות הן