גרף הפונקציה טנגנס
בערך זהסימון מתמטי .
טנגנס (מסומן כ-
tan
{\displaystyle \tan }
tg
{\displaystyle {\text{tg}}}
פונקציה טריגונומטרית בסיסית.
במשולש זה, טנגנס הזווית A שווה
a
b
{\displaystyle {\frac {a}{b}}}
בהגדרתה הבסיסית ביותר, פונקציית הטנגנס מציינת, כפונקציה של זווית , את היחס במשולש ישר-זווית בין הניצב שמול הזווית לניצב שלידה. הגדרה זאת מתייחסת רק לזווית בתחום שבין 0 ל-90 מעלות או
π
2
{\displaystyle {\frac {\pi }{2}}}
רדיאנים . משולשים עם זוויות זהות דומים ויחס הצלעות בהם תמיד זהה. לכן הטנגנס של זווית מוגדר היטב .
כמו כן, נפוץ מאוד השימוש בפונקציית הטנגנס כמנה של סינוס וקוסינוס בעלי אותה זווית. קל להגיע לזהות זו באמצעות הצבת היחסים שמייצגות פונקציות הסינוס והקוסינוס:
{
sin
x
=
a
c
cos
x
=
b
c
tan
x
=
sin
x
cos
x
⟺
tan
x
=
a
/
c
b
/
c
=
a
b
{\displaystyle {\begin{cases}\sin x={a \over c}\\\cos x={b \over c}\\\tan x={\sin x \over \cos x}\end{cases}}\Longleftrightarrow \ \tan x={a/c \over b/c}={a \over b}}
תמונה זאת מדגימה את הדרך השנייה להגדיר טנגנס. ניתן להרחיב את הטנגנס לכל זווית ממשית באמצעות מעגל היחידה , כאשר הרדיוס "מסתובב" נגד כיוון השעון כמספר הזווית (אם היא שלילית אז עם כיוון השעון). קיימות שתי דרכים לעשות זאת:
טנגנס הזווית שווה ליחס בין שיעור ה-y של קצה הרדיוס (הסינוס של הזווית) לשיעור ה-x שלה (הקוסינוס של הזווית):
tan
x
=
sin
x
cos
x
{\displaystyle \tan x={\frac {\sin x}{\cos x}}}
מעבירים למעגל משיק מהנקודה (1,0), וממשיכים את הרדיוס. שיעור ה-y של הנקודה בה הם נחתכים שווה לטנגנס הזווית. פונקציה הטנגנס אינה מוגדרת עבור
x
=
π
2
+
π
k
{\displaystyle \ x={\frac {\pi }{2}}+\pi k}
k
{\displaystyle \ k}
מספר שלם , כיוון שבדרך הראשונה, הקוסינוס שווה ל-0 (ומתקבלת חלוקה באפס ), ובדרך השנייה הרדיוס מקביל למשיק ולא חותך אותו.
ניתן להגדיר את הפונקציה באמצעות טור טיילור :
tan
x
=
∑
n
=
1
∞
B
2
n
(
−
4
)
n
(
1
−
4
n
)
(
2
n
)
!
x
2
n
−
1
for
|
x
|
<
π
2
{\displaystyle \tan x=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}\quad {\mbox{ for }}\left|x\right|<{\frac {\pi }{2}}}
B
n
{\displaystyle \ B_{n}}
מספר ברנולי ה-n.
הצגה מפורשת לתחילת הטור:
tan
x
=
x
+
1
3
x
3
+
2
15
x
5
+
17
315
x
7
+
⋯
,
for
|
x
|
<
π
2
{\displaystyle \tan x=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots ,\qquad {\text{for }}|x|<{\frac {\pi }{2}}}
בדומה לפונקציית הקוסינוס שמתקבלת מפונקציית הסינוס על ידי הזווית המשלימה לזווית ישרה, ניתן גם להגדיר את פונקציית הקוטנגנס:
cot
x
=
tan
(
π
2
−
x
)
{\displaystyle \cot x=\tan \left({\frac {\pi }{2}}-x\right)}
tan
(
π
2
−
x
)
=
1
tan
x
{\displaystyle \tan \left({\frac {\pi }{2}}-x\right)={\frac {1}{\tan x}}}
הופכי של הטנגנס.
פונקציית הטנגנס היא פונקציה אי זוגית , משום שמתקיים
tan
(
−
x
)
=
−
tan
(
x
)
{\displaystyle \tan \ (-x)=-\tan \ (x)}
לפונקציה יש מחזור של
π
{\displaystyle \ \pi }
הפונקציה מוגדרת לכל x, מלבד
x
=
π
2
+
π
k
{\displaystyle \ x={\frac {\pi }{2}}+\pi k}
k
{\displaystyle \ k}
אסימפטוטות אנכיות של הפונקציה.
הפונקציה רציפה , גזירה ואינטגרבילית בכל נקודה שבה היא מוגדרת. הפונקציה עולה בכל קטע שבו היא מוגדרת, ואין לה נקודות קיצון .
לפונקציה אינסוף שורשים מהצורה
x
=
π
k
{\displaystyle \ x=\pi k}
k
{\displaystyle \ k}
לפי כלל המנה , נגזרת הפונקציה היא:
d
d
x
tan
x
=
d
d
x
(
sin
x
cos
x
)
=
sin
x
⋅
sin
x
+
cos
x
⋅
cos
x
cos
2
x
=
1
cos
2
x
{\displaystyle {\operatorname {d} \! \over \operatorname {d} \!x}\tan x={\operatorname {d} \! \over \operatorname {d} \!x}\left({\frac {\sin x}{\cos x}}\right)={\frac {\sin x\cdot \sin x+\cos x\cdot \cos x}{\cos ^{2}x}}={\frac {1}{\cos ^{2}x}}}
הקדומה של הפונקציה היא:
∫
tan
x
d
x
=
−
ln
|
cos
x
|
+
C
{\displaystyle \int \tan x\,dx=-\ln |\cos x|+C}
זהויות טריגונומטריות פונקציית הטנגנס מקיימת:
tan
(
−
θ
)
=
−
tan
θ
{\displaystyle \ \tan(-\theta )=-\tan \theta }
tan
(
π
−
θ
)
=
−
tan
θ
{\displaystyle \ \tan(\pi -\theta )=-\tan \theta }
בעזרת פונקציית הטנגנס אפשר לבטא את חמש הפונקציות הבסיסיות האחרות (השורשים יכולים להיות חיוביים ושליליים):
sin
θ
=
tan
θ
1
+
tan
2
θ
{\displaystyle \sin \theta ={\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}}
,
cos
θ
=
1
1
+
tan
2
θ
{\displaystyle \cos \theta ={\frac {1}{\sqrt {1+\tan ^{2}\theta }}}}
,
cot
θ
=
1
tan
θ
{\displaystyle \cot \theta ={1 \over \tan \theta }}
,
csc
θ
=
1
+
tan
2
θ
tan
θ
{\displaystyle \csc \theta ={{\sqrt {1+\tan ^{2}\theta }} \over \tan \theta }}
,
sec
θ
=
1
+
tan
2
θ
{\displaystyle \sec \theta ={\sqrt {1+\tan ^{2}\theta }}}
סכום זוויות:
tan
(
θ
±
φ
)
=
tan
θ
±
tan
φ
1
∓
tan
θ
tan
φ
{\displaystyle \tan(\theta \pm \varphi )={\frac {\tan \theta \pm \tan \varphi }{1\mp \tan \theta \tan \varphi }}}
זווית כפולה:
tan
2
θ
=
2
tan
θ
1
−
tan
2
θ
{\displaystyle \tan 2\theta ={\frac {2\tan \theta }{1-\tan ^{2}\theta }}\,}
,
tan
3
θ
=
3
tan
θ
−
tan
3
θ
1
−
3
tan
2
θ
{\displaystyle \tan 3\theta ={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}}
חצי זווית:
tan
θ
2
=
csc
θ
−
cot
θ
=
±
1
−
cos
θ
1
+
cos
θ
=
sin
θ
1
+
cos
θ
=
1
−
cos
θ
sin
θ
{\displaystyle \tan {\tfrac {\theta }{2}}=\csc \theta -\cot \theta =\pm \,{\sqrt {1-\cos \theta \over 1+\cos \theta }}={\frac {\sin \theta }{1+\cos \theta }}={\frac {1-\cos \theta }{\sin \theta }}}
ממוצע זוויות:
tan
(
α
+
β
2
)
=
sin
α
+
sin
β
cos
α
+
cos
β
=
−
cos
α
−
cos
β
sin
α
−
sin
β
{\displaystyle \tan \left({\frac {\alpha +\beta }{2}}\right)={\frac {\sin \alpha +\sin \beta }{\cos \alpha +\cos \beta }}=-\,{\frac {\cos \alpha -\cos \beta }{\sin \alpha -\sin \beta }}}
אם x , y , ו-z הן שלוש זוויות של משולש כלשהו, כלומר אם
=
π
=
x
+
y
+
z
{\displaystyle \ =\pi =x+y+z}
חצי מעגל (180°), אזי:
tan
(
x
)
+
tan
(
y
)
+
tan
(
z
)
=
tan
(
x
)
tan
(
y
)
tan
(
z
)
{\displaystyle \ \tan(x)+\tan(y)+\tan(z)=\tan(x)\tan(y)\tan(z)}
פונקציות טריגונומטריות הפוכות גרף פונקציית הארכטנגנס הפונקציה ההפוכה לפונקציית הטנגנס נקראת ארקטנגנס ומסומנת
arctan
{\displaystyle \ \arctan }
tan
−
1
{\displaystyle \ \tan ^{-1}}
חד-חד-ערכית , ניתן להחליט איזה טווח ערכים היא תקבל. נהוג להגדיר אותה לטווח הערכים
(
−
π
2
,
π
2
)
{\displaystyle \ (-{\frac {\pi }{2}},{\frac {\pi }{2}})}
d
d
x
arctan
x
=
1
1
+
x
2
{\displaystyle {d \over dx}\arctan x={1 \over 1+x^{2}}}
משפט הטנגנסים משפט הטנגנסים הוא משפט המציין תכונה של צלעות וזוויות במשולש . אם שתיים מהצלעות הן
a
,
b
{\displaystyle \ a,b}
α
,
β
{\displaystyle \ \alpha ,\beta }
a
−
b
a
+
b
=
tan
[
1
2
(
α
−
β
)
]
tan
[
1
2
(
α
+
β
)
]
{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}}




 ערך מורחב – זהויות טריגונומטריות
ערך מורחב – זהויות טריגונומטריות ערך מורחב – פונקציות טריגונומטריות הפוכות
ערך מורחב – פונקציות טריגונומטריות הפוכות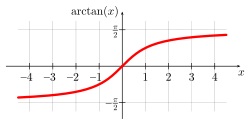
 ערך מורחב – משפט הטנגנסים
ערך מורחב – משפט הטנגנסים







































![{\displaystyle {\frac {a-b}{a+b}}={\frac {\tan[{\frac {1}{2}}(\alpha -\beta )]}{\tan[{\frac {1}{2}}(\alpha +\beta )]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b2c685e57123416d7f2f4a816786d80eb2b183b)