משפט רול
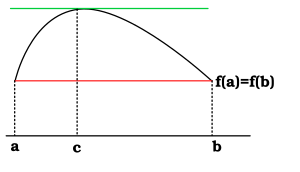
משפט רול (על שם המתמטיקאי הצרפתי מישל רול שניסח אותו ב-1691), הוא משפט בסיסי בחשבון אינפיניטסימלי, העוסק בתכונה של פונקציות רציפות וגזירות בקטע סגור. המשפט אומר כי אם פונקציה רציפה בקטע סגור , גזירה בקטע הפתוח וערכיה בשני קצוות הקטע זהים, כלומר , אז קיימת נקודה c בקטע כך ש-, כלומר המשיק לגרף הפונקציה בנקודה זו הוא קו מאוזן ושיפועו שווה ל-0.
מבחינה לא פורמלית ניתן לתאר את המשפט כך: אם מצוירת פונקציה בין שתי נקודות באותו גובה (אותו ערך של ) בלי שהעיפרון מורם מהדף ובלי היווצרות 'שפיצים', תהיה לפחות נקודה אחת שבה העיפרון נע בדיוק במקביל לציר ה-x, ולא בשיפוע זוויתי כלשהו.
המשפט
[עריכת קוד מקור | עריכה]תהי פונקציה רציפה בקטע הסגור וגזירה בקטע הפתוח . אם מתקיים , אז קיימת נקודה כך שמתקיים .
הוכחה
[עריכת קוד מקור | עריכה]על פי משפט ויירשטראס השני, פונקציה רציפה בקטע סגור מקבלת בו מינימום ומקסימום. אם גם המינימום וגם המקסימום מתקבלים בקצוות (אשר, לפי הנתון, שווים בערכם) הרי שהפונקציה קבועה בקטע , והנגזרת שלה היא אפס בכל נקודה בקטע . אחרת, המקסימום או המינימום מתקבלים בתוך הקטע ובכל אחד מהמקרים קיימת נקודת קיצון בקטע . לפי תנאי המשפט, הפונקציה גזירה ב- ובפרט היא גזירה ב-, ולכן על פי משפט פרמה ערך הנגזרת ב- הוא אפס כנדרש.
הכללות
[עריכת קוד מקור | עריכה]אף שהמשפט נדמה כמעט טריוויאלי, קיימות לו שתי הכללות שימושיות מאוד: משפט הערך הממוצע של לגראנז' ומשפט הערך הממוצע של קושי.
קישורים חיצוניים
[עריכת קוד מקור | עריכה]- משפט רול, באתר MathWorld (באנגלית)
- משפט רול, באתר אנציקלופדיה למתמטיקה (באנגלית)
- משפט רול, באתר אנציקלופדיה בריטניקה (באנגלית)

![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)






