גדילה מעריכית

גדילה מעריכית או צמיחה אקספוננציאלית (באנגלית: Exponential Growth) הוא תהליך שמתאר גדילה כמותית כתלות בזמן. גדילה זו מתרחשת כאשר הקצב הרגעי של השינוי הכמותי (אשר ניתן לתיאור על ידי הנגזרת של הפונקציה הכמותית), פרופורציונלי לכמות עצמה.

פונקציה המתארת גדילה מעריכית מיוצגת על ידי אקספוננט, זאת בשונה מפונקציות אחרות המתארות גדילה, כגון פרבולה או ישר.

אם קבוע הפרופורציה המתאר את הגדילה הוא בעל סימן שלילי, אזי נהוג לומר כי מדובר בדעיכה מעריכית ולא בגדילה. במקרה שהמרחב מעליו מוגדרת הפונקציה הוא מרחב בדיד ולא רציף, ההתנהגות הפונקציונלית מכונה גדילה גאומטרית או דעיכה גאומטרית, מאחר שערכי הפונקציה ניתנים למיפוי כטור גאומטרי.

הנוסחה לגדילה מעריכית עבור משתנה $x(t_{n})$ שמוגדר מעל זמן בדיד (סדרת הרגעים $t_{n}=0,1,2...,n$) שקצב הגדילה שלו הוא $r$, נתונה על ידי:

$x(t_{n})=x_{0}(1+r)^{t_{n}}$

כאשר $x_{0}$ מוגדר להיות ערך המשתנה $x$ בראשית הזמן.

גדילה שכזו מתקיימת בתחומים שונים בחיי היומיום, ובהם: הפצת זיהום נגיפי, תפיחה של חוב לאור ריבית דריבית וכן התפשטות של סרטונים ויראליים ברשת האינטרנט.

במקרים אלה ונוספים, הגדילה המעריכית איננה מתמשכת לעד, אלא מאט החל משלב מסוים לאור קיומם של חסמים עליוניים חיצוניים (למשל, קיומה של אוכלוסייה סופית או מגבלות מרחביות שונות), והגדילה הופכת להיות גדילה לוגיסטית.

גדילה מעריכית מכונה לעיתים בשם השגוי "גדילה מהירה", אלא שגדילה מעריכית עשויה גם להיות איטית.

דוגמאות

ביולוגיה

מושבת E-coli שמציגה גדילה אקספוננציאלית תחת תנאים אופטימליים

• בתרביות של מיקרואורגניזמים, מספר הישויות יגדל בקצב אקספוננציאלי עד שחומרי המזון בתרבית יגמרו. בדרך כלל האורגניזם הראשון בתרבית מתפצל לשני אורגניזמים, שכל אחד מהם מתפצל לשניים כך שנוצרים ארבעה חדשים. התפצלותם של הארבעה מובילה ליצירת שמונה חדשים, וכן הלאה. מכיוון שגדילה מעריכי מצביע על קצב צמיחה קבוע, ההנחה היא שתאים הגדלים באופן אקספוננציאלי נמצאים במצב יציב. דוגמה לחלוקת אורגניזמים כזו היא תהליך יצירת עובר, שבו הזיגוטה מתחלקת בחלוקה מיטוטית לאחר ההפריה, ומספר התאים גדל בקצב אקספוננציאלי.
• בהנחה שאין חיסון זמין, נגיפים (למשל נגיף הקורונה או אבעבועות שחורות) בדרך כלל מתפשטים באוכלוסייה בקצב אקספוננציאלי. כל אדם נגוע יכול להדביק מספר אנשים חדשים.

כלכלה

• צמיחה כלכלית מוגדרת באחוזים, מה שמרמז על גדילה מעריכית.
• ריבית דריבית על השקעה בריבית קבועה מספקת צמיחה מעריכית של ההון.
• תרמיות פירמידה בנויות כך שכל חבר חדש מצרף מספר חברים, וכתוצאה מכך הן מציגות צמיחה מעריכית. הדבר מביא לרווחים גבוהים אצל המשקיעים הראשונים בתרמית, ולהפסדים בקרב מספר רב של משקיעים שלא היו מראשוני המצטרפים.

אינטרנט

גרף המתאר את מספר הצפיות היומי של הסרטון גנגנם סטייל

• תוכן אינטרנטי, כגון ממים או סרטונים, יכול להתפשט בצורה מעריכית. פעמים רבות מתארים את התוכן כ"וויראלי", כאנלוגיה להתפשטות נגיפים. השימוש המודרני במדיה החברתית מאפשר לאדם יחיד להעביר תוכן כלשהו לאנשים רבים בו זמנית. כל אחד מהאנשים הללו עשוי להמשיך ולהפיץ את התוכן לאנשים רבים וכן הלאה. כתוצאה מכך נגרמת התפשטות מהירה מאוד של התוכן. לדוגמה, הסרטון גנגנם סטייל הועלה ליוטיוב ב-15 ביולי 2012, והגיע למאות אלפי צפיות ביום הראשון, למיליונים ביום העשרים, ובמצטבר הוא נצפה על ידי מאות מיליונים בתוך פחות מחודשיים.

תיאור מתמטי

גדילה מעריכית עם הקבועים a=3, b=2, r=5

הגודל $x$ תלוי מעריכית בזמן אם ניתן לומר כי:

$x(t)=a\cdot b^{t/\tau }$

כאשר הקבוע $a$ מתאר את ערכו ההתחלתי של הגודל $x$:

$x(0)=a$

הקבוע $b$ הוא פקטור גדילה חיובי, בעוד $\tau$ הוא קבוע המתאר את משך הזמן הדרוש עבור $x(t)$ להכפיל את עצמו $b$ פעמים:

$x(t+\tau )=a\cdot b^{\frac {t+\tau }{\tau }}=a\cdot b^{\frac {t}{\tau }}\cdot b^{\frac {\tau }{\tau }}=x(t)\cdot b$

אם $\tau >0$ ו-$b>1$, אז מדובר בגדילה מעריכית. אם $\tau <0$ ו-$b>1$, או לחלופין $\tau >0$ ו-$0<b<1$ הרי שמדובר בדעיכה מעריכית.

דעיכה מעריכית עם הקבועים: a=24, b=1/2, r=5

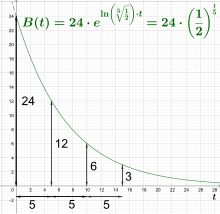
דוגמה

אם אוכלוסיית חיידקים מכפילה את גודלה בכל עשר דקות, והאוכלוסייה ההתחלתית מונה חיידק אחד בלבד, כמה חיידקים יהיה בכלי לאחר שעה אחת?

מנתוני השאלה ניתן להסיק כי $a=1$ (זו האוכלוסייה ההתחלתית), $b=2$ (זהו קבוע ההכפלה), ו-$\tau =10$ (זהו משך הזמן הנדרש להכפלת האוכלוסייה פי 2).

נציב את המספרים בנוסחה לגדילה המעריכית ונקבל:

$x(t=60)=1\cdot 2^{60\min /10\min }=2^{6}=64$

כלומר בסך הכל יהיו 64 חיידקים מקץ שעה אחת.

זוגות רבים של הקבועים $b,\tau$ (כאשר $b$ הוא מספר אי-שלילי חסר יחידות ו-$\tau$ הוא קבוע בעל יחידות של זמן), מייצגים בדיוק את אותו קצב הגדילה, כאשר $\tau$ פרופורציונלי ל-$\log _{a}b$. מכאן, שניתן לכתוב את ההתנהגות הפונקציונלית של הגדילה באופנים רבים השקולים זה לזה, למשל:

$x(t)=x_{0}\cdot e^{kt}=x_{0}\cdot e^{\frac {t}{\tau }}=x_{0}\cdot 2^{\frac {2}{T}}=x_{0}\cdot (1+{\frac {r}{100}})^{\frac {t}{p}}$

כאשר $x_{0}$ היא הכמות ההתחלתית. בכל צעד הוחלף הבסיס המעריכי, ובהתאם נבחרו קבועי זמן אחרים:

• קבוע הגדילה $k$ מתאר את התדירות (מספר הפעמים ליחידת זמן) שבה הכמות גדלה פי פקטור $e$. בכלכלה, קבוע זה נקרא בשמות "תשואה לוגריתמית", או "תשואה בריבית רציפה".
• קבוע הגדילה $\tau$ מתאר את הזמן הנדרש עבור הכמות לגדול פי פקטור $e$.
• קבוע הגדילה $T$ מתאר את הזמן הנדרש עבור הכמות לגדול פי 2.
• הקבוע $r$ הוא אחוז הגדילה (מספר חסר ממדים) במהלך מחזור $p$ כלשהו.

וניתן לקשור בצורה חד-חד-ערכית בין כל הקבועים הללו (הקשר נגזר מהפעלת לוגריתם טבעי על כל אגפי השקילות):

$k={\frac {1}{\tau }}={\frac {\ln 2}{T}}={\frac {\ln(1+{\frac {r}{100}})}{p}}$

כאשר $k=0$ שקול ל-$r=0$ ול-$\tau ,T$ אינסופיים.

אם $p$ מתאר את יחידת הזמן בבעיה (למשל, דקות או שעות), אז השבר $t/p$ מייצג את מספר יחידות הזמן. במקום להשתמש בסימון $t$ עבור מספר יחידות הזמן (שהוא גודל חסר ממדים) במקום משתנה הזמן עצמו, ניתן להחליף את הגודל $t/p$ במשתנה $t$ בלבד (שבו הזמן מיוצג ביחידות אמיתיות). לשם האחידות, הסימון המוצע איננו בשימוש במסגרת ערך זה. כך שבמקרה לעיל, החלוקה ב-$p$ היא לא חלוקה נומרית גרידא, אלא המרה של מספר חסר ממדים למספר בעל ממדים.

שיטת קירוב פופולרית לחישוב זמן ההפכלה מתוך אחוז הגדילה, היא "כלל ה-70", לפיו $T\simeq 70/r$. בקירוב אחר, המונה הוא 72.

גרפים המשווים את זמני ההכפלה ואת זמני מחצית החיים של גדילות מעריכיות (בקווים בולטים) ושל דעיכות מעריכיות (קווים מקווקווים), וכן את קירובי ה-70 וה-72 שלהם

ייצוג לוג-ליניארי

אם משתנה $x$ גדל בצורה אקספוננציאלית וניתן לייצוג על פי הנוסחה $x(t)=x_{0}(1+r)^{t}$, אזי $log(x)$ גדל ליניארית, בכל בסיס לוגריתמי. ניתן לראות זאת באמצעות הוצאת לוגריתם משני אגפי המשוואה: $log(x)=log(x_{0})+t\cdot log(1+r)$.

הדבר מאפשר למדל משתנה שגדל בצורה אקספוננציאלית באמצעות מודלים לוג-ליניאריים. לדוגמה, אם נדרשת הערכה אמפירית של קצב הגדילה של משתנה $x$ ביחס לזמן, ניתן לבצע רגרסיה ליניארית על הלוגריתם של המשתנה $x$, ביחס לזמן $t$.

המשוואה הדיפרנציאלית

מתוך הפונקציה המעריכית $x(t)=x_{0}e^{kt}$ ניתן לגזור את המשוואה הדיפרנציאלית הליניארית הבאה:

${\frac {dx}{dt}}=kx$

דהיינו, השינוי הרגעי של הגודל $x$ ביחס לזמן $t$, פרופורציונלי לערכו של $x(t)$.

על ידי הפרדת משתנים וביצוע אינטגרל בשני אגפי המשוואה הדיפרנציאלית, ניתן לחזור לתצורה המקורית:

${\begin{aligned}{\frac {dx}{dt}}&=kx\\[5pt]{\frac {dx}{x}}&=k\,dt\\[5pt]\int _{x(0)}^{x(t)}{\frac {dx}{x}}&=k\int _{0}^{t}\,dt\\[5pt]\ln {\frac {x(t)}{x(0)}}&=kt.\end{aligned}}$

כך שאכן נקבל:

$x(t)=x_{0}e^{kt}$

ואילו $k<0$, הרי שלפנינו דעיכה מעריכית.

עבור שינוי לא ליניארי של מודל הגדילה ראו פונקציה לוגיסטית.

קצבי גדילה אחרים

קיימים מספר סדרי גודל של קצבי גדילה, כאשר כל הפונקציות ששייכות למשפחת גדילה אחת תמיד תשאפנה לאינסוף מהר יותר מפונקציות ששייכות למשפחה אחרת, בהינתן שמשפחת הפונקציות שואפת מהר יותר לאינסוף. לדוגמה, בטווח הארוך, גדילה מעריכית מהירה יותר מכל גדילה לינארית (הבסיס למלתוסיאניזם) וגם מכל גדילה פולינומית. כלומר, לכל $\alpha$ מתקיים $\lim _{t\rightarrow \infty }{t^{\alpha } \over ae^{t}}=0$. בפועל קיים רצף של קצבי גדילה, וניתן למצוא קצבי צמיחה שנמצאים בין שני אלו מבחינת מהירות השאיפה שלהם לאינסוף, כלומר הם איטיים מצמיחה מעריכית, ומהירים מצמיחה לינארית.

קיימים גם קצבי צמיחה מהירים יותר מקצב אקספוננציאלי. כאשר פונקציית צמיחה שואפת לאינסוף בזמן סופי, היא מכונה צמיחה היפרבולית . בין הצמיחה האקספוננציאלית לבין הצמיחה ההיפרבולית קיימות משפחות צמיחה נוספות ששואפות לאינסוף מהר מפונקציות אקספוננציאליות, למשל היפר-פעולות כמו טטרציה, והאלכסון של פונקציית אקרמן, $A(n,n)$.

צמיחה לוגיסטית

ערך מורחב – פונקציה לוגיסטית

בדוגמאות מציאותיות שמתנהגות בצורה אקספוננציאלית, הצמיחה האקספוננציאלית הראשונית לרוב אינה נמשכת לנצח. במקרים כאלו, לאחר תקופה כלשהי של גדילה בקצב אקספוננציאלי, קצב הגדילה מאט בהשפעת גורמים חיצוניים או סביבתיים. לדוגמה, הגידול של אוכלוסייה מסוימת עשוי להיות חסום על ידי גבול עליון בשל מגבלות משאבים. בשנת 1845, המתמטיקאי הבלגי פייר פרנסואה ורהולסט הציג לראשונה מודל מתמטי של צמיחה כזו, שנקראת "צמיחה לוגיסטית".

מגבלות המודל

מודלים של גדילה מעריכית המתארים תופעות פיזיקליות, ניתנים ליישום בצורה מוגבלת, שכן גדילה בלתי מוגבלת איננה תואמת את המציאות.

על אף שגדילה עשויה להיות מעריכית בתחילתה, התופעה המתוארת תתקדם לבסוף לאזור שבו פקטורי משוב שליליים יהפכו למשמעותיים (מה שיוביל למודל גדילה לוגיסטית), או שהנחות מובלעות של המודל המעריכי, כגון רציפות או משוב מיידי, יאבדו ממשמעותן.

דוגמה מובהקת למגבלות של מודל גדילה מעריכית, ניתן למצוא בחוק ריילי-ג'ינס לקרינת גוף שחור. עבור אורכי גל קצרים, עוצמת הקרינה שואפת לאינסוף, בניגוד לחוק שימור האנרגיה (מה שכונה בשם "הקטסטרופה של העל-סגול"). הניסוח המשלים לאורכי גל קצרים מצוי בחוק וין, והניסוח הכללי ביותר, המאחד את כלל אורכי הגל, מצוי בחוק פלאנק.