קרינת גוף שחור

בפיזיקה, גוף שחור הוא עצם אידיאלי הבולע באופן מושלם קרינה אלקטרומגנטית בכל אורכי הגל, ללא החזרה או העברה. גוף שחור פולט קרינה אלקטרומגנטית באופן התלוי אך ורק בטמפרטורה שלו, על פי חוק פלאנק. קרינה זו מכונה קרינת גוף שחור. הקרינה הנפלטת אינה תלויה בקרינה הפוגעת, פרט להשפעה של זו על טמפרטורת הגוף. גוף שחור אידיאלי הוא קירוב טוב לתיאור הקרינה הנפלטת מגופים חמים רבים: אור השמש, נורת להט וקרינת תת־אדום מבעלי חיים.
גוף שחור קורן בכל אורכי הגל, בעוצמה התלויה באורך הגל ובטמפרטורה, בהתאמה לחוק פלאנק. גוף שחור בטמפרטורה הנמוכה מכ־700 מעלות קלווין (430 מעלות צלזיוס) פולט מעט מאוד קרינה באור הנראה, וקורן בעיקר בתדירויות נמוכות יותר, כמו גלי רדיו, מיקרו ותת־אדום.
הסיבה לצורה של נוסחת פלאנק היא יצירתם של הפוטונים באנרגיות בדידות, כלומר קוונטות. הבנה זו, יחד עם הסבר האפקט הפוטואלקטרי, היוו את תחילתה של תורת הקוונטים.
במציאות, גוף שחור מתאר בקירוב טוב משטחים רבים, בעיקר משטחים טבעיים. קיימים גם מכשירים המדמים גוף שחור בדיוק גבוה, לשימושים תעשייתיים ומדעיים.
החיפוש אחר מודל מתמטי של קרינת גוף שחור[עריכת קוד מקור | עריכה]
אלקטרומגנטיות קלאסית וחוק ריילי ג'ינס[עריכת קוד מקור | עריכה]
בתחילה לא היה ידוע מה גורם לפליטת הקרינה באורכי הגל השונים; בתחילת המאה ה־20 פותחה נוסחה באופן אמפירי (על ידי ניסויים) המתארת את ספקטרום הפליטה של הגוף השחור, בכל אורכי הגל, עבור טמפרטורה נתונה. נוסחה זו נקראת חוק ריילי־ג'ינס על שם מפתחיה, ג'ון ויליאם סטראט ריילי וג'יימס ג'ינס (James Jeans):
כאשר היא עוצמת הקרינה הנפלטת, הוא אורך הגל של הקרינה הנפלטת, הוא קבוע בולצמן ו־ היא הטמפרטורה בקלווין.
כאשר מבצעים סכימה על משוואה זו מאפס ועד אינסוף, מתקבל כי הפליטה הכוללת בכל אורכי הגל היא אינסופית, דבר שאינו תואם את חוק שימור האנרגיה. אי התאמה זו בין החישובים למציאות מכונה "הקטסטרופה של העל־סגול", מכיוון שהנוסחה כן מתאימה לאורכי הגל ארוכים יותר, אך מתבדרת בתחום של העל־סגול.
כתוצאה מ"קטסטרופה" זו החליטו להגביל נוסחה זו לתחום אורכי הגל הארוכים ונמצאה נוסחה חדשה לאורכי הגל הקצרים, בשם חוק וין (גם היא באופן אמפירי).
תורת הקוונטים וחוק פלאנק[עריכת קוד מקור | עריכה]
לבסוף אוחדו שתי הנוסחאות על ידי מקס פלאנק, למשוואת פלאנק, לפי תדירות הקרינה:
או לפי אורך הגל של הקרינה:
- .
בפיתוח נוסחה זו הניח פלאנק כי האנרגיה נפלטת מגוף שחור במנות בדידות של אנרגיה (קוונטים של אנרגיה):
כאשר הוא קבוע פלאנק, היא תדירות הקרינה ו־ הוא מספר טבעי. כלומר, מנות האנרגיה הן כפולות של מנה בסיסית, התלויה בתדירות בלבד. הנחה זו היא אחת ההנחות הבסיסיות שהביאו לפיתוח תורת הקוונטים.
תיאור מיקרוסקופי לקרינת גוף שחור[עריכת קוד מקור | עריכה]
לרוב מטפלים בקרינת גוף שחור במבט מאקרוסקופי ולא במבט מיקרוסקופי. עקב פלקטואציות (תזוזות קלות) משיווי המשקל של אטומי החומר (לפי התיאור של מודל לורנץ) נפלטת קרינה עקב התאוצה של האלקטרונים. ניתן לראות זאת בנוסף במתכות מהתפלגות פרמי-דיראק, כאשר ישנה טמפרטורה, האלקטרונים "מקפצים" להם בין המצבים.
התפלגות פלאנק[עריכת קוד מקור | עריכה]
 ערך מורחב – חוק פלאנק
ערך מורחב – חוק פלאנק
חוק פלאנק הוא חוק שנוסח בידי מקס פלאנק בשנת 1900, ומתאר את התפלגות הקרינה של גוף שחור. התפלגות פלאנק מכילה את כל המידע על הקרינה, וניתן לגזור ממנה את החוקים הנוספים של קרינת גוף שחור, המתוארים בהמשך.
התפלגות זו מתוארת על ידי עקומה המתאימה עוצמת הקרינה (או למעשה צפיפות ההספק) הנפלטת על ידי הגוף לכל אורך גל או תדירות. הגרף המתאר את תלות עוצמת הקרינה בתדירות נקרא "ספקטרום קרינה של גוף שחור". למעשה, ניתן לפתח את משוואת פלנק מתוך פונקציית צפיפות האנרגיה , כמתואר להלן:
התפלגות צפיפות האנרגיה של הקרינה ליחידת תדירות נתונה על ידי:
כאשר הוא קבוע פלאנק ו־ הוא התדירות.
הקרינה מתפשטת לכל הכיוונים במהירות האור , והזווית המרחבית שבה מתפשטת הקרינה היא , שהיא הזווית המרחבית המקסימלית. לפיכך, מטעמי איזוטרופיות וסימטריה נובע ששטף האנרגיה ליחידת תדירות הוא
וזהו חוק פלאנק.
הקשר בין צפיפות לפי תדר וצפיפות לפי אורך גל[עריכת קוד מקור | עריכה]
את חוק פלאנק ניתן לנסח כתלות בתדר וגם כתלות באורך הגל . בהינתן גל בתדר ואורך ערכים אלה אינם שווים. במקום זה מתקיים
- .
הסיבה לכך היא ש מיצג את הגבול כש- שואף ל של שטף הקרינה בתחום התדרים חלקי . בעוד ש מיצג את הגבול כש- שואף ל של שטף הקרינה בתחום אורכי הגל חלקי . תחום אורכי הגל מתאים בקרוב לתחום התדרים , ומכאן המקדם בקשר בין הנוסחאות. אם בוחרים פרמטר שונה לתיאור הגל (למשל התדר בסקאלה לוגוריתמית) יהיה צורך להכפיל במקדם מתאים.
במילים אחרות איננו פונקציה במובן המצומצם, אלא הוא מגדיר מידה במרחב התדרים (באופן פורמלי יותר, מדובר בנגזרת רדון ניקודים של מידת שטף הקרינה ביחס למידת התדר), ומכאן שכאשר מבצעים החלפת משתנים יש להכפיל בערכה המוחלט של הנגזרת של פונקציית המעבר.
חוק ההסחה של וין[עריכת קוד מקור | עריכה]
אם מסמנים את פונקציית צפיפות שטף הקרינה הנפלטת מגוף בטמפרטורה על ידי מתקבל כי
- .
מכאן שגרף הפליטה של גוף שחור נראה אותו דבר בכל טמפרטורה לאחר שינוי קנה מידה מתאים (בתדר ובצפיפות השטף). עובדה זאת התגלתה אמפירית לפני חוק פלאנק ונקראת חוק ההסחה של וין. ניתן לחשב נומרית את המקסימום של הפונקציה ולראות שהוא מתקבל ב. מכאן שהתדר בו גוף שחור בטמפרטורה קורן בעוצמה מקסימלית הוא
- .
באופן דומה אורך הגל שבו גוף שחור בטמפרטורה קורן בעוצמה מקסימלית הוא
- .
גם לשתי המשוואות האחרונות קוראים לעיתים חוק ההסחה של וין. התדר ואורך הגל אינם מתאימים לאותו גל. זאת בגלל המקדם המתואר למעלה.
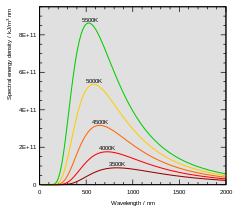
באופן איכותי, חוק ההסחה של וין אומר שככל שמחממים את הגוף השחור לטמפרטורה גבוהה יותר, כך יתקצר אורך הגל שבו נפלטת הקרינה המרבית (ראו הגרף למעלה). כך למשל, כדי להגיע לפליטה ששיאה במרכז התחום הנראה (אורך גל של כ־550 ננומטר), נדרשת טמפרטורה של כ־5,300 קלווין.
חוק זה מאפשר מדידת טמפרטורה של גוף שחור (או גוף שחור בקירוב) באמצעות מדידת ספקטרום הקרינה התרמי שלו (ספקטרום קרינת גוף שחור). מאחר שכוכבים רבים הם בקירוב גוף שחור, שיטה זו מאפשרת להעריך את טמפרטורת הכוכבים.
להתפלגות תכונה נוספת: גוף שחור בטמפרטורה גבוהה יותר יפלוט קרינה בעוצמה גבוהה יותר, בכל אורכי הגל, מאשר גוף שחור בטמפרטורה נמוכה יותר.
גוף אפור ואמיסיביות[עריכת קוד מקור | עריכה]
במציאות לא קיים גוף שחור אידיאלי, אך נוח להשתמש במודל גוף שחור והוא משמש קירוב טוב לחומרים רבים בטווח רחב של אורכי גל. חומרים רבים קורנים באופן דומה לגוף שחור, אך ביעילות קטנה מ־1 וקבועה בקירוב. ניתן לעשות שימוש במדד האמיסיביות לתיאור היחס שבין הפליטה של גוף אפור לפליטה של גוף שחור. על פי חוק קירכהוף יחס זה זהה למקדם הבליעה של הגוף. האמיסיביות בדרך כלל איננה מספר קבוע אלא פונקציה של אורך הגל (או התדירות) והטמפרטורה, אך במקרים רבים היא קבועה לטווח צר מסוים, למשל באורכי גל של מצלמה תרמית 3–5 מיקרון או בטווח 8–12 מיקרון.
חוק סטפן בולצמן[עריכת קוד מקור | עריכה]
חוק סטפן־בולצמן קובע כי שטף הקרינה הנפלט מגוף שחור הוא מתכונתי לחזקה הרביעית של הטמפרטורה שלו. החוק נוסח באופן אמפירי על ידי הפיזיקאים יוזף סטפן ותלמידו לודוויג בולצמן באופן נפרד ועצמאי, כתוצאה מתצפיות בקרינת גוף שחור. הניסוח המתמטי של החוק הוא:
כאשר הוא קבוע סטפן־בולצמן,
שטף האנרגיה הכולל של הגוף נקרא גם "הבהיקות הנקודתית" של גוף, ניתן לחישוב גם על ידי סכימה (אינטגרל) של השטף בכל התדירויות או אורכי הגל מאפס ועד אינסוף
כאשר השטף נתון על ידי התפלגות פלאנק.
חוק זה התגלה אמפירית עוד לפני התיקון של פלאנק. ברם, מכיוון שקבוע הפרופורציה תלוי בקבוע פלאנק הקוונטי, לא ניתן היה לחשב באמצעות התאוריה הקלאסית גודל זה, אלא רק למדוד אותו בניסוי.
לחץ קרינה[עריכת קוד מקור | עריכה]
תוצאה חשובה נוספת היא שלחץ הקרינה שווה לשליש מצפיפות האנרגיה: . תוצאה זו מתקבלת גם ממציאת משוואת המצב של גז יחסותי.
גוף שחור מלאכותי[עריכת קוד מקור | עריכה]
עבור שימושים מדעיים ותעשייתיים, נדרש לעיתים מקור קרינה המדמה גוף שחור. לעיתים נדרש רק מקור בעל התפלגות קרינה ידועה, ובמקרה זה ניתן להשתמש למשל בנורת להט שהיא גוף שחור מצוין בכל תחום אורכי הגל הנראה ותת־אדום. קיימות נורות המכוילות בזרם חשמלי מסוים להיות בטמפרטורה מדויקת, למשל 2850 קלווין שהיא נורה סטנדרטית. לטמפרטורות גבוהות יותר, עד 3200 קלווין, ניתן להשתמש בנורת הלוגן.
כאשר נדרשים, בנוסף להתפלגות הקרינה, גם אחידות קרינה מפני שטח מסוים, או סך של עוצמה מדויקת, משתמשים ב"גופים שחורים" תעשייתיים. לגופים הללו משתמשים בצבע שחור מיוחד שנשאר "שחור", כלומר בולע מאוד, בתחום רחב של אורכי גל מעל־סגול ועד תת־אדום. גופים אלו ניתנים לחימום או קירור לטמפרטורה מדויקת (אלפית מעלה צלזיוס ואף פחות) באחידות גבוהה.
גוף שחור שקוע (cavity blackbody) הוא בדרך כלל גוף מחומר מתכתי או קרמי מחומם, בעל שקע בצורת חרוט קעור, המצופה בצבע שחור מתאים. פתח החרוט הוא המשטח שנחשב לגוף השחור, ובדרך כלל מהווה קירוב מצוין עם אמיסיביות מעל 0.99, וקוטר קטן בדרך כלל עד 5 ס"מ. גופים אלו גם מגיעים לטמפרטורות גבוהות של מעל 1000 מעלות צלזיוס.
גוף שחור מישורי עשוי בדרך כלל מפלטת נחושת הניתנת לחימום וקירור, מצופה בצבע שחור מתאים. גופים אלו יכלים להיות גדולים יותר, עד כחצי מטר לגוף סטנדרטי, אך טווח הטמפרטורה נמוך יותר והאמיסיביות (מידת הקירוב לגוף שחור אידיאלי) נמוכה יותר בדרך כלל. גופים אלו משמשים למשל לכיול האחידות של מצלמה תרמית.
ראו גם[עריכת קוד מקור | עריכה]
- תת־אדום
- קרינת הרקע הקוסמית
- אמצעי ראיית לילה
- דיאגרמת הרצשפרונג-ראסל - הקשר בין צבע לטמפרטורת כוכב
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- Blackbody Spectrum - הדגמה של קרינת גוף שחור - ניתן לקבוע טמפרטורה ולצפות באור המתקבל ובגרף הפליטה (באנגלית)
























![{\displaystyle [\nu ,\nu +\varepsilon ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e78c6a6df148cb30c0b81d341d02fea894164018)
![{\displaystyle [\lambda ,\lambda +\varepsilon ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbe673f916bfd574371d93cd2700447e89d990a3)
![{\displaystyle [\nu -{\frac {c}{\lambda ^{2}}}\varepsilon ,\nu ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbf64fe1598b02d34e44a83902df8e6f49aea864)









![{\displaystyle \lambda _{\mathrm {max} }={\frac {2.9\times 10^{-3}[mK]}{T}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/344fd5e6c89be95a41230f2d4143aac20c54d639)




![{\displaystyle \ \sigma ={\frac {2{{\pi }^{5}}k_{B}^{4}}{15{{c}^{2}}{{h}^{3}}}}=5.670400(40)\times {{10}^{-8}}\ [{\text{J}}{{\text{s}}^{-1}}{{\text{m}}^{-2}}{{\text{K}}^{-4}}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e304cc7a7e99f0d73ab54e5ba06f233f710c5cd)

