התפלגות פרמי-דיראק

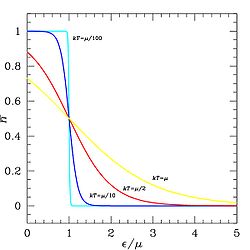
התפלגות פרמי-דיראק משורטטת עבור טמפרטורות שונות. ככל שהטמפרטורה נמוכה יותר כך ההתפלגות קרובה יותר לפונקציית מדרגה.

התפלגות פרמי-דיראק (או סטטיסטיקת פרמי-דיראק) היא פונקציית התפלגות סטטיסטית בעזרתה ניתן לתאר תכונות של חלקיקים פרמיונים זהים חסרי אינטראקציה. ההתפלגות קרויה על שם הפיזיקאים אנריקו פרמי ופול דיראק.

הגדרה

באופן מפורש, האכלוס הממוצע של רמת אנרגיה מסוימת במערכת של פרמיונים זהים הנמצאת בשיווי משקל תרמודינמי נתון על ידי הפונקציה הבאה:

$$n_{FD}(\epsilon )={\frac {1}{e^{(\epsilon -\mu )/k_{B}T}+1}}$$ כאשר:

• $\ n_{FD}$ הוא המספר הממוצע של חלקיקים שימצאו במצב (או לחלופין ההסתברות למציאת חלקיק במצב).
• $\ \epsilon$ היא האנרגיה של מצב זה.
• $\ \mu$ הוא הפוטנציאל הכימי.
• $\ T$ היא הטמפרטורה.
• $\ k_{B}$ הוא קבוע בולצמן.

בעזרת פונקציה זו, ובעזרת צפיפות מצבים $\ g(\epsilon )$, ניתן לחשב תכונות תרמודינמיות שונות של המערכת. לדוגמה, האנרגיה הממוצעת נתונה על ידי: $$\ U=\int \epsilon g(\epsilon )n_{FD}(\epsilon )d\epsilon$$

פיתוח

את התפלגות פרמי-דיראק ניתן לקבל בקלות על ידי שימוש בצבר הגרנד קנוני. במסגרת צבר זה, ההסתברות למציאת מערכת במצב i עם $\ N_{i}$ חלקיקים ואנרגיה כוללת $\ E_{i}$ נתונה על ידי $P_{i}={\frac {1}{\mathcal {Z}}}e^{-{\frac {(E_{i}-\mu N_{i})}{k_{B}T}}}$, כאשר ${\mathcal {Z}}=\sum _{i}e^{-{\frac {(E_{i}-\mu N_{i})}{k_{B}T}}}$ היא פונקציית החלוקה הגרנד-קנונית.

ניקח כמערכת רמת אנרגיה (חד-חלקיקית) מסוימת $\epsilon$. אם אין אינטראקציה בין החלקיקים $\ E_{i}=n\epsilon$ כאשר $\ n=N_{i}$ הוא מספר החלקיקים הנמצאים ברמה זו. אם מדובר בפרמיונים, בגלל עקרון האיסור של פאולי ייתכן רק $\ n=0,1$. פונקציית החלוקה במקרה זה תהיה ${\mathcal {Z}}=1+e^{-{\frac {(\epsilon -\mu )}{k_{B}T}}}$. מכאן ניתן לקבל את מספר החלקיקים הממוצע על ידי שימוש ב$\langle n\rangle =\sum _{n}nP(n)$, או על ידי $\langle n\rangle =-{\frac {\partial \Omega }{\partial \mu }}$ כאשר $\Omega =-k_{B}T\ln {\mathcal {Z}}$.

תכונות ההתפלגות

• מתקיים $\ n_{FD}(\epsilon )\leq 1$ . דבר זה מבטא את עקרון האיסור של פאולי - שני פרמיונים זהים לא יכולים להיות באותו מצב. בפרט המספר הממוצע של פרמיונים בכל מצב קטן (או שווה) מאחד.

• בגבול של טמפרטורה נמוכה ( $\ T\to 0$) התפלגות פרמי-דיראק שואפת לפונקציית מדרגה, בה כל הרמות בעלות אנרגיה $\ \epsilon <\mu =\epsilon _{F}$ מאוכלסות, ואילו כל הרמות בעלות אנרגיה $\ \epsilon >\mu =\epsilon _{F}$ אינן מאוכלסות. האנרגיה המקסימלית של המצבים המאוכלסים מסומנת $\ \epsilon _{F}$ ונקראת אנרגיית פרמי.

קישורים חיצוניים

מדיה וקבצים בנושא התפלגות פרמי-דיראק בוויקישיתוף

• התפלגות פרמי-דיראק, באתר אנציקלופדיה בריטניקה (באנגלית)