התפלגות כי בריבוע
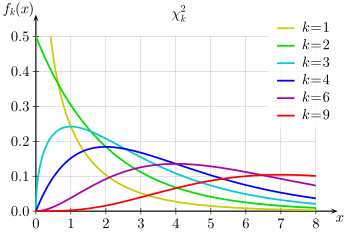
| פונקציית צפיפות ההסתברות | |
 | |
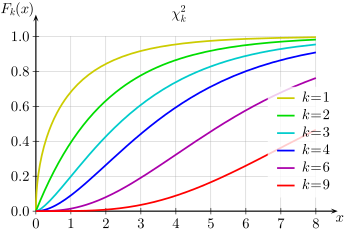
| פונקציית ההסתברות המצטברת | |
|---|---|
 | |
| מאפיינים | |
| פרמטרים | (ידוע כ"דרגות חופש") |
| תומך | |
|
פונקציית צפיפות הסתברות (pdf) | |
|
פונקציית ההסתברות המצטברת (cdf) | |
| תוחלת | |
| סטיית תקן | |
| חציון | |
| ערך שכיח | |
| שונות | |
| אנטרופיה | |
|
פונקציה יוצרת מומנטים (mgf) | |
| פונקציה אופיינית | |
| צידוד | |
| גבנוניות | |
התפלגות כי בריבוע (, נהגה בכ' רפה, לעיתים נכתב חי בריבוע) היא התפלגות בעלת חשיבות רבה בסטטיסטיקה. חשיבותה העיקרית בהסקה סטטיסטית נובעת מהעובדה שתחת הנחות סבירות, גדלים הניתנים לחישוב באופן פשוט מתפלגים בקירוב בהתאם להתפלגות זו תחת השערת האפס. בין היתר, ההתפלגות משמשת כבסיס למבחן כי בריבוע. השם "כי בריבוע" מקורו באות היוונית , כי.
הגדרה[עריכת קוד מקור | עריכה]
בהינתן מספר טבעי (כלומר, שלם וחיובי), נאמר כי למשתנה מקרי רציף יש התפלגות כי בריבוע עם דרגות חופש, אם צפיפות ההסתברות שלו נתונה בביטוי
כאשר היא פונקציית גמא.
במקרה כזה, מסמנים .
קשר להתפלגויות אחרות[עריכת קוד מקור | עריכה]
בהינתן משתנים מקריים בלתי תלויים, שלכולם התפלגות נורמלית סטנדרטית (כלומר: התפלגות נורמלית עם תוחלת 0 ושונות 1), המשתנה
מתפלג כי בריבוע עם דרגות חופש.
התפלגות כי בריבוע היא מקרה פרטי של התפלגות גמא, עם פרמטר צורה ופרמטר קצב .
| התפלגויות | ||
|---|---|---|
| התפלגויות בדידות כלליות | אחידה בדידה • בינומית • מולטינומית • בינומית שלילית • ברנולי • גאומטרית • היפרגאומטרית • היפרגאומטרית שלילית • מנוונת • פואסון |  |
| התפלגויות רציפות כלליות | אחידה רציפה • בטא • גמא • לוג-נורמלית • מעריכית (אקספוננציאלית) • נורמלית (גאוסית) • לפלס • משולשת • פארטו • ריילי • קושי • כי בריבוע | |
| התפלגויות בפיזיקה סטטיסטית | בולצמן • בוז-איינשטיין • מקסוול-בולצמן • פרמי-דיראק • זטא | |
| התפלגויות נוספות | התפלגות t • התפלגות F • ארלנג • וייבול • לוגיסטית | |
| סוגי התפלגויות | בדידה • רציפה • מותנית • נורמלית מוכללת • זנב עבה • לא פריקה • משותפת | |
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- התפלגות כי בריבוע, באתר MathWorld (באנגלית)
























