משתמש:בר/טיוטת חשבון דיפרנציאלי

במתמטיקה, חישוב דיפרנציאלי תת תחום בחדו"א החוקר את השיעורים בהם משתנים הכמויות. [1] זה אחד משני התחומים העיקריים לצד, חשבון אינטגרלי - החווקר את האזור שמתחת ל עקומה. [2]
מושאי המחקר העיקריים בחישוב דיפרנציאלי הם נגזרת של פונקציה, רעיונות קשורים כמו הדיפרנציאל, ויישומיהם. הנגזרת של פונקציה בערך קלט שנבחר מתארת את קצב השינוי של הפונקציה ליד אותו ערך קלט. תהליך מציאת נגזרת נקרא בידול . מבחינה גיאומטרית הנגזרת בנקודה היא שיפוע קו המשיק לתרשים של הפונקציה באותה נקודה, בתנאי שהנגזרת קיימת ומוגדרת באותה נקודה. עבור פונקציה אמיתית של משתנה אמיתי יחיד, נגזרת הפונקציה בנקודה קובעת בדרך כלל את הקירוב הליניארי הטוב ביותר לפונקציה באותה נקודה.
חישוב דיפרנציאלי וחישוב אינטגרלי מחוברים על ידי המשפט הבסיסי של החשבון, הקובע כי בידול הוא התהליך ההפוך לאינטגרציה .
לנגזרות יש שימושים כמעט בכל התחומים הכמותיים. לדוגמה, בפיזיקה, נגזרת העתק של גוף נע ביחס לזמן היא מהירות הגוף, ונגזרת המהירות ביחס לזמן היא תאוצה. נגזרת המומנטום של גוף ביחס לזמן שווה לכוח המופעל על הגוף; סידור מחדש של אמירה נגזרת זו מוביל ל F = m המפורסם F משוואה הקשורה לחוק התנועה השני של ניוטון . קצב התגובה של תגובה כימית הוא נגזרת. במחקרי תפעול, נגזרים קובעים את הדרכים היעילות ביותר להובלת חומרים ומפעלים לעיצוב.
נגזרות משמשות לעתים קרובות למציאת נקודון קיצון של פונקציה. משוואות הכרוכות בנגזרות נקראות משוואות דיפרנציאליות והן בסיסיות בתיאור תופעות טבע . נגזרים והכללותיהם מופיעים בתחומים רבים של מתמטיקה, כמו ניתוח מורכב, ניתוח פונקציונאלי, גיאומטריה דיפרנציאלית, תיאוריה של מדדים ואלגברה מופשטת .
נגזרת[עריכת קוד מקור | עריכה]

נני ח ש- x ו- y הם מספרים אמיתיים וכי y הוא פונקציה של x, כלומר לכל ערך של x, יש ערך מתאים של y . ניתן לכתוב קשר זה כ- y = f ( x ) . אם f ( x ) היא המשוואה לקו ישר (נקרא משוואה ליניארית ), ישנם שני מספרים אמיתיים m ו- b כך y = mx + b . ב"צורת יירוט מדרון "זו מכונה המונח m המדרון וניתן לקבוע אותו מהנוסחה:
גכאשר הסמל Δ (צורת האותיות הגדולות של האות הדלתית היוונית ) הוא קיצור של "שינוי פ נימה". מכאן עולה כי Δy = m Δ x .
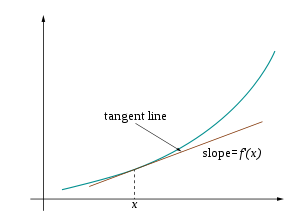
פונקציה כללית אינה קו ולכן אין לה שיפוע. מבחינה גיאומטרית, הנגזרת של f בנקודה x = a היא שיפוע קו המשיק לפונקציה f בנקודה a (ראה איור). לעיתים קרובות זה מצוין f ′ ( a ) בתמצית Lagrange או dy / dx | x = a בציון של לייבניץ . מכיוון שהנגזרת היא שיפוע הקירוב הליניארי ל- f בנקודה a, הנגזרת (יחד עם ערך f ב- a ) קובעת את הקירוב הליניארי הטוב ביותר, או ליניאריזציה, של f בסמוך לנקודה a .
אם לכל נקודה a בתחום ה- f יש נגזרת, יש פונקציה ששולחת כל נקודה a לנגזרת של f ב- a . לדוגמה, אם f ( x ) = x 2, פונקצית הנגזרת f ′ ( x ) = dy / dx = 2 x .
רעיון שקשור בקשר הדוק הוא ההפרש של פונקציה. כאשר x ו- y הם משתנים אמיתיים, הנגזרת של f ב- x היא המדרון של קו המשיק לתרשים של f ב- x . מכיוון שהמקור והיעד של f הם חד ממדיים, הנגזרת של f היא מספר אמיתי. אם x ו- y הם ווקטורים, הקירוב הליניארי הטוב ביותר לגרף f תלוי באופן בו f משתנה בכמה כיוונים בבת אחת. נקיטת הקירוב הליניארי הטוב ביותר לכיוון בודד קובעת נגזרת חלקית, המסומנת בדרך כלל ∂y / ∂ x . לינאריזציה של f לכל הכיוונים בבת אחת מכונה הנגזרת הכוללת .
היסטוריית של הנגזרת[עריכת קוד מקור | עריכה]
הרעיון של נגזרת במובן של קו משיק הוא אחד עתיק והיה מוכר כבר ביוון העתיקה לגאומטרים כמו אוקלידס (כ -300 לפני הספירה), ארכימדס (בערך 287–212 לפנה"ס) ואפולוניוס מפרגה (בערך 262–2002) 190 לפני הספירה). ארכימדס הציג גם שימוש באינפיניטסימלים, אם כי אלה שימשו בעיקר לחקר אזורים ונפחים ולא נגזרות ומשיקים (ראו את השימוש של ארכימדס באינפיניטסימלים).
השימוש באינפיניטסימלים ללמוד שיעורי השינוי ניתן למצוא המתמטיקה ההודית, אולי 500 לספירה, כאשר האסטרונום והמתמטיקאי Aryabhata (476-550) השתמש באינפיניטסימלים כדי ללמוד את מסלולו של הירח . השימוש באינפיניטסימלים לחישוב שיעורי השינוי פותח באופן משמעותי על ידי Bhāskara II ( 1114–1185 ); ואכן, נטען [3] כי ניתן למצוא בעבודותיו רבות ממושגי המפתח לחישוב דיפרנציאלי, כגון " משפט רול ". [4]
המתמטיקאי האסלאמי, שרף אל-דין אל-תיסי (1135–1213), קבע בתמורת המשוואות שלו תנאים לכמה משוואות מעוקבות כדי לקבל פתרונות, על ידי מציאת המקסימום של פולינומים מעוקבים מתאימים. הוא הוכיח, למשל, כי המקסימום של המעוקב - x 3 מתרחש כאשר x = 2 a / 3, והסיק ממנו כי למשוואה 2 - x 3 = c יש בדיוק פיתרון חיובי אחד כאשר c = 4 a 3 27 /, וכן שני פתרונות חיוביים בכל פעם 0 < <c <4 3/27. [5] ההיסטוריון של המדע, ראשדי ראשד, [6] טען כי אל-טיסי כנראה השתמש בנגזרת של הקוביה כדי להשיג תוצאה זו. עם זאת, טוענים חוקרים אחרים כי מסקנתו של ראשד טענה שהוא יכול היה להשיג את התוצאה בשיטות אחרות שאינן מחייבות את נגזרת הפונקציה. [7]
ההתפתחות המודרנית של החישוב זוכה בדרך כלל לאייזק ניוטון (1643–1727) ול גוטפריד וילהלם לייבניץ (1646–1716), שסיפקו גישות עצמאיות [8] ואחדות לבידול ונגזרות. עם זאת, התובנה העיקרית שזכתה להם בזכות זו הייתה המשפט הבסיסי בחישוב הנוגע לבידול ואינטגרציה: הדבר איבד את השיטות הקודמות ביותר למחשבי אזורים ונפחים, [9] שלא הוארך משמעותית מאז זמנו של אבן אל. -היתם ( אלחאזן ). [10] לרעיונותיהם בנושא נגזרים, ניוטון ולייבניץ נבנו על עבודות קודמות משמעותיות של מתמטיקאים כמו פייר דה פרמה (1607-1665), אייזק בארו (1630–1677), רנה דקארט (1596–1650), כריסטיאן הויגנס (1629–1695) ), בלז פסקל (1623–1662) וג'ון ואליס (1616–1703). בנוגע להשפעתו של פרמה, ניוטון כתב פעם במכתב כי "היה לי הרמז לשיטה זו [של שטף] מהדרך של פרמה לשרטט משיקים, ועל ידי החלתה על משוואות מופשטות, באופן ישיר ובלתי הפיך, הפכתי אותה לכללית"[11]. לרוב ניתן לאיסק בארו קרדיט לפיתוח המוקדם של הנגזרת. [12] אף על פי כן, ניוטון ולייבניץ נותרו דמויות מפתח בתולדות הדיפרנציליות, לא מעט משום שניוטון היה הראשון ליישם בידול לפיזיקה תיאורטית, ואילו לייבניץ פיתח באופן שיטתי חלק גדול מהציון שעדיין נעשה בו שימוש כיום.
מאז המאה ה -17 מתמטיקאים רבים תרמו לתורת ההבחנה. במאה ה -19 הוחלף החשבון על בסיס מתוחכם הרבה יותר על ידי מתמטיקאים כמו אוגוסטין לואי קוצ'י (1789–1857), ברנהרד רימן (1826–1866) וקארל וויירשטראס (1815–1897). זה היה גם בתקופה זו שהוכללה ההכללה לחלל האוקלידי ולמטוס המורכב .
יישומים של נגזרים[עריכת קוד מקור | עריכה]
אופטימיזציה[עריכת קוד מקור | עריכה]
אם f היא פונקציה גזירה על ℝ (או מרווח פתוח ) ו- x היא מקסימלית מקומית או מינימום מקומי של f אזי הנגזרת של f לפי x היא אפס. נקודות בהן f' ( x ) = 0 נקראות נקודות קריטיות או נקודות נייחות (והערך של f ב- x נקרא ערך קריטי ). אם לא מניחים ש- f ניתן להבחין בכל מקום אחר, נקודות נקודתיות שבהן הוא אינו מצליח להבחין, נקראות גם נקודות קריטיות.
אם f נבדל פעמיים, לעומת זאת ניתן לנתח נקודה קריטית x של f ידי התחשבות בנגזרת השנייה של f ב- x :
- אם זה חיובי, x הוא מינימום מקומי;
- אם הוא שלילי, x הוא מקסימום מקומי;
- אם הוא אפס, x יכול להיות מינימום מקומי, מקסימום מקומי או לא. (לדוגמה, ל- f ( x ) = x 3 יש נקודה קריטית ב- x = 0, אך אין בה לא מקסימום ולא מינימום, ואילו ל- f ( x ) = ± x 4 יש נקודה קריטית ב- x = 0 ו- מינימום ומקסימום, בהתאמה, שם. )
זה נקרא מבחן הנגזר השני . גישה חלופית, המכונה מבחן הנגזרת הראשון, כוללת בחינת סימן ה- f' מכל צד של הנקודה הקריטית.
לקיחת נגזרים ופתרון לנקודות קריטיות היא אפוא דרך פשוטה למצוא מינימות או מקסימות מקומיות, שיכולות להועיל במיטוב . לפי משפט הערך הקיצוני, פונקציה רציפה במרווח סגור חייבת להשיג את ערכי המינימום והמקסימום שלה לפחות פעם אחת. אם ניתן להבחין בפונקציה, המינימום והמקסימה יכולים להתרחש רק בנקודות או בנקודות קצה קריטיות.
יש לכך גם יישומים ברישום הגרפים: ברגע שנמצאו המינימום והמקסימה המקומית של פונקציה ניתנת להבחנה, ניתן להשיג עלילה גסה של הגרף מתוך התצפית שהיא תגדל או תקטן בין נקודות קריטיות.
במימדים גבוהים יותר, נקודה קריטית של פונקציה מוערכת בסולם היא נקודה בה מדרגת הצבע היא אפס. ניתן עדיין להשתמש במבחן הנגזר השני לניתוח נקודות קריטיות על ידי התחשבות בערכי העצמיות של המטריצה הסית של נגזרות חלקיות שנייה של הפונקציה בנקודה הקריטית. אם כל הערכים העצמיים הם חיוביים, הנקודה היא מינימום מקומי; אם כולם שליליים, זהו מקסימום מקומי. אם יש כמה ערכי עצמיים חיוביים וחלקם השליליים, הנקודה הקריטית נקראת " נקודת אוכף ", ואם אף אחד מהמקרים האלה לא מתקיים (כלומר, חלק מערכי העצמי הם אפס), המבחן נחשב כלא חד משמעי.
חישוב וריאציות[עריכת קוד מקור | עריכה]
דוגמה אחת לבעיית מיטוב היא: מצא את העקומה הקצרה ביותר בין שתי נקודות על גבי משטח, בהנחה שהעקומה חייבת לשכב גם על המשטח. אם המשטח הוא מטוס, הרי שהעקומה הקצרה ביותר היא קו. אבל אם המשטח, למשל, בצורת ביצה, הרי שהדרך הקצרה ביותר אינה ברורה מייד. נתיבים אלה נקראים גיאודזיקה, ואחת הבעיות הבסיסיות ביותר בחישוב הווריאציות היא מציאת גיאודזיקה. דוגמא נוספת היא: מצא את מילוי פני השטח הקטן ביותר בעקומה סגורה בחלל. משטח זה נקרא משטח מינימלי וגם ניתן למצוא אותו באמצעות חשבון הווריאציות.
פיזיקה[עריכת קוד מקור | עריכה]
לחישוב יש חשיבות חיונית בפיזיקה: תהליכים פיזיקליים רבים מתוארים על ידי משוואות הכוללות נגזרות, המכונות משוואות דיפרנציאליות . הפיזיקה דואגת במיוחד לאופן בו כמויות משתנות ומתפתחות לאורך זמן, והמושג " נגזרת הזמן " — קצב השינוי לאורך זמן — חיוני להגדרה המדויקת של כמה מושגים חשובים. בפרט, נגזרות הזמן של מיקום האובייקט הן משמעותיות בפיזיקה הניוטונית :
- המהירות היא הנגזרת (ביחס לזמן) של העקירה של האובייקט (מרחק מהמיקום המקורי)
- תאוצה היא הנגזרת (ביחס לזמן) של מהירות האובייקט, כלומר הנגזרת השנייה (ביחס לזמן) של מיקום האובייקט.
לדוגמה, אם מיקום האובייקט בקו ניתן על ידי
אז מהירות האובייקט היא
והתאוצה של האובייקט היא
שהוא קבוע.
משוואות דיפרנציאליות[עריכת קוד מקור | עריכה]
משוואה דיפרנציאלית היא קשר בין אוסף פונקציות לנגזרות שלהם. משוואת דיפרנציאל רגילה היא משוואה דיפרנציאלית המתייחסת פונקציות של משתנה אחד לנגזרות שלהם ביחס לאותו משתנה. משוואה דיפרנציאלית חלקית היא משוואה דיפרנציאלית המתייחסת פונקציות של יותר ממשתנה אחד לנגזרות החלקיות שלהם. משוואות דיפרנציאליות מתרחשות באופן טבעי במדעי הפיזיקה, במודל מתמטי, ובתוך המתמטיקה עצמה. לדוגמא, החוק השני של ניוטון, המתאר את הקשר בין האצה לכוח, יכול להיות מצוין כמשוואת ההפרש הרגילה
משוואת החום במשתנה חלל אחד, המתארת כיצד החום מתפזר דרך מוט ישר, היא משוואת ההפרש החלקית
כאן u ( x, t ) הוא הטמפרטורה של המוט במצב x והזמן t ו- α הוא קבוע שתלוי עד כמה חום מתפזר דרך המוט.
משפט הערך הממוצע[עריכת קוד מקור | עריכה]

משפט הערך הממוצע נותן קשר בין ערכי הנגזרת לערכים של הפונקציה המקורית. אם f (x) היא פונקצית ערכים אמיתית a ו- b הם מספר a <b, אזי הערך הממוצע המשפט אומר כי תחת שערות מתונות, המדרון שבין שתי הנקודות ( f (א)) ו (, f ( b )) שווה למדרון של קו המשיק ל- f בנקודה מסוימת c בין a ל b . במילים אחרות,
בפועל, מה שמשפט הערך הממוצע עושה הוא לשלוט בפונקציה מבחינת הנגזרת שלה. למשל, נניח של- f יש נגזרת שווה לאפס בכל נקודה. משמעות הדבר היא שקו המשיק שלו אופקי בכל נקודה, ולכן הפונקציה צריכה להיות גם אופקית. משפט הערך הממוצע מוכיח שזה חייב להיות נכון: המדרון בין שתי נקודות כלשהן בגרף f חייב להיות שווה למדרון של אחד מקווי המשיק של f . כל המדרונות הללו הם אפסיים, ולכן לכל קו מנקודה אחת בגרף לנקודה אחרת יהיה גם שיפוע אפס. אבל זה אומר שהפונקציה לא זזה מעלה או מטה, ולכן עליה להיות קו אופקי. תנאים מורכבים יותר על הנגזרת מובילים למידע פחות מדויק אך עדיין שימושי מאוד על הפונקציה המקורית.
פולינומים של טיילור וסדרות טיילור[עריכת קוד מקור | עריכה]
הנגזרת נותנת את הקירוב הליניארי הטוב ביותר האפשרי לפונקציה בנקודה נתונה, אך זה יכול להיות שונה מאוד מהפונקציה המקורית. אחת הדרכים לשפר את הקירוב היא לקחת קירוב ריבועי. כלומר, לינאריזציה של פונקציה אמיתית מוערכת f ( x ) בנקודה x 0 היא פולינום ליניארי a + b ( x - x 0 ), וייתכן שניתן לקבל קירוב טוב יותר על ידי שיקול ריבועי פולינום a + b ( x - x 0 ) + c ( x - x 0 ) 2 . עדיף שעוד עשוי להיות פולינום מעוקב a + b ( x - x 0 ) + c ( x - x 0 ) 2 + d ( x - x 0 ) 3, ואת הרעיון הזה ניתן להרחיב לפולינומים בדרגה שרירותית. לכל אחד מהפולינומים הללו, צריכה להיות הבחירה הטובה ביותר של מקדמים a, b, c ו- d, שהופכת את הקירוב לטוב ככל האפשר.
בשנות ה השכונה של x 0, a הבחירה הטובה ביותר הוא f תמיד f 0), ועבור b הבחירה הטובה ביותר האפשרית היא תמיד f' 0). עבור מקדמים c, d גבוהה יותר, מקדמים אלה נקבעים על ידי נגזרים גבוהים יותר של f . c צריך תמיד להיות f'' ( x 0 ) / 2, ו- d תמיד צריך להיות f''' ( x 0 ) / 3! . השימוש במקדמים אלה מעניק לפולינום של טיילור של f . הפולינום של טיילור בדרגה d הוא הפולינום של התואר d הטובה ביותר ל- f, ואת המקדמים שלו ניתן למצוא על ידי הכללה של הנוסחאות לעיל. המשפט של טיילור נותן גבול מדויק לכמה טוב הקירוב. אם f הוא פולינום בדרגה פחות או שווה ל- d, אז פולינום טיילור של תואר d שווה ל- f .
גבול הפולינומים של טיילור הוא סדרה אינסופית הנקראת סדרת טיילור . סדרת טיילור היא לעיתים קרובות קירוב טוב מאוד לפונקציה המקורית. פונקציות השוות לסדרת טיילור שלהם נקראות פונקציות אנליטיות . אי אפשר לפונקציות עם אי-רציפות או פינות חדות להיות אנליטיים, אך יש פונקציות חלקות שאינן אנליטיות.
משפט פונקציה מרומז[עריכת קוד מקור | עריכה]
לא ניתן לצייר כמה צורות גיאומטריות טבעיות, כגון עיגולים, כגרף של פונקציה . למשל, אם f ( x, y ) = x 2 + y 2 - 1, המעגל הוא הקבוצה של כל הזוגות (x, y ) כך ש- f ( x, y ) = 0 . קבוצה זו נקראת מערך האפס של f, והיא אינה זהה לתרשים f, שהוא פרבוליד . משפט הפונקציה המרומז ממיר יחסים כמו f ( x, y ) = 0 לפונקציות. הוא קובע שאם f ניתנת f ברציפות, אז סביב רוב הנקודות, מערך האפס של f נראה כמו גרפים של פונקציות שהודבקו יחד. הנקודות בהן הדבר אינו נכון נקבעות על ידי תנאי בנגזרת של f . ניתן להדביק את המעגל יחד מהגרפים של שתי הפונקציות ± √ 1 - x 2 . בשכונה של כל נקודה במעגל למעט (−1, 0) ו (1, 0), באחת משתי הפונקציות הללו יש גרף שנראה כמו המעגל. (שתי הפונקציות הללו נפגשות במקרה (−1, 0) ו- (1, 0), אך הדבר אינו מובטח על ידי משפט הפונקציה המרומז. )
משפט הפונקציה המרומז קשור קשר הדוק למשפט הפונקציה ההפוכה, הקובע כי פונקציה נראית כמו גרפים של פונקציות בלתי הפיכות שהודבקו יחד.
ראו גם[עריכת קוד מקור | עריכה]
- דיפרנציאלי (חשבון)
- גיאומטריה דיפרנציאלית
- בידול מספרי
- טכניקות לבידול
- רשימת נושאי חשבון
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ "Definition of DIFFERENTIAL CALCULUS". www.merriam-webster.com (באנגלית). נבדק ב-2020-05-09.
- ^ "Definition of INTEGRAL CALCULUS". www.merriam-webster.com (באנגלית). נבדק ב-2020-05-09.
- ^ Ian G. Pearce. Bhaskaracharya II.
- ^ Broadbent, T. A. A.; Kline, M. (באוקטובר 1968). "Reviewed work(s): The History of Ancient Indian Mathematics by C. N. Srinivasiengar". The Mathematical Gazette. 52 (381): 307–8. doi:10.2307/3614212. JSTOR 3614212.
{{cite journal}}: (עזרה) - ^ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), pp. 304-309.
- ^ Cited by J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), pp. 304-309.
- ^ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), pp. 304-309.
- ^ Newton began his work in 1666 and Leibniz began his in 1676. However, Leibniz published his first paper in 1684, predating Newton's publication in 1693. It is possible that Leibniz saw drafts of Newton's work in 1673 or 1676, or that Newton made use of Leibniz's work to refine his own. Both Newton and Leibniz claimed that the other plagiarized their respective works. This resulted in a bitter Newton Leibniz calculus controversy between the two men over who first invented calculus which shook the mathematical community in the early 18th century.
- ^ This was a monumental achievement, even though a restricted version had been proven previously by James Gregory (1638–1675), and some key examples can be found in the work of Pierre de Fermat (1601–1665).
- ^ Victor J. Katz (1995), "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3): 163-174 [165-9 & 173-4]
- ^ Sabra, A I. (1981). Theories of Light: From Descartes to Newton. Cambridge University Press. p. 144. ISBN 978-0521284363.
- ^ Eves, H. (1990).
- J. Edwards (1892). Differential Calculus. London: MacMillan and Co. p. 1.







![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)



