כריסטיאן הויגנס
 | |
| לידה |
14 באפריל 1629 האג, הרפובליקה ההולנדית |
|---|---|
| פטירה |
8 ביולי 1695 (בגיל 66) האג, הרפובליקה ההולנדית |
| ענף מדעי | אסטרונומיה, פיזיקה, מתמטיקה |
| מקום מגורים | הולנד, צרפת |
| מקום קבורה |
Grote of Sint-Jacobskerk |
| מקום לימודים |
|
| מנחה לדוקטורט |
Frans van Schooten, Jan Jansz de Jonge Stampioen |
| מוסדות |
האקדמיה הצרפתית למדעים |
| תלמידי דוקטורט |
גוטפריד וילהלם לייבניץ |
| פרסים והוקרה |
עמית החברה המלכותית |
| תרומות עיקריות | |
|
הסבר על טבעות שבתאי, כח צנטריפוגלי, נוסחאות התנגשות, שעון מטוטלת, עקרון הויגנס, תורת הגלים, מנוע הויגנס, שבירה כפולה, עינית הויגנס, משפט שטיינר-הויגנס וגילוי ירח שבתאי טיטאן | |
כריסטיאן הויגנס (בהולנדית: ⓘ?, מבוטא הויחנס או האוחנס; 14 באפריל 1629 – 8 ביולי 1695) היה פיזיקאי, מתמטיקאי, אסטרונום וממציא הולנדי, יליד האג. מחלוצי המדע ומהמדענים הבולטים במאה ה-17.
עבודתו כללה תצפיות טלסקופ, רישום ותיאור של טבעות שבתאי ואת תגליתו של ירחו טיטאן, המצאת שעון המטוטלת ושיטות אחרות לבקרת זמן. בפיזיקה פיתח את התאוריה לפיה טיבו של האור גלי ואינו מורכב מחלקיקים, בניגוד לתיאורו של אייזק ניוטון, הדמות המרכזית בימיו הראשונים של המדע הממוסד. בכך היה בר הפלוגתא המרכזי לפרדיגמה האופטית שנתקבעה באותן שנים והייתה תקפה עד ניסוי שני הסדקים שהגה וביצע תומאס יאנג ב-1801, בו הוכחה תפיסת האור כגל של הויגנס כנכונה. הוא פרסם מחקרים רבים ומשמעותיים נוספים באופטיקה ובמכניקה, ועבודה חלוצית בענף ההסתברות בניסוח מתמטי של משחקי מזל. בשל כל אלה מזוהה כאחת מדמויות המפתח במהפכה המדעית ובהגות המודרנית.
ראשית ימיו והשכלתו[עריכת קוד מקור | עריכה]

כריסטיאן הויגנס נולד למשפחת האצולה הויגנס, אביו קונסטנטין הויגנס, היה מזכירם של הנסיכים לבית אורנז' פרדריק הנדריק ווילם השני, שהיו למעשה הישות השולטת בארצות השפלה. אביו, קונסטנטין היה גם משורר ומלחין לעת מצוא מוערך. סבו היה מזכירו של וילם השתקן. אמו של כריסטיאן נפטרה כשהיה בן שמונה בעקבות הולדת אחותו, סוזן.
כריסטיאן נולד בהאג, בשיאה של התקופה המוכרת כתור הזהב של הולנד. כבן למשפחת אצולה מלומדת רכש את השכלתו בבית, בעזרת אביו, מורים פרטיים ובפרט על ידי המתמטיקאי יאן סטמפיון. הוא רכש השכלה נרחבת בתחומים שונים – אריתמטיקה, גאומטריה, ענפים מתמטיים נוספים, גאוגרפיה, לוגיקה, לטינית, יוונית, צרפתית, ואיטלקית. בגיל 14 החל הויגנס לגלות עניין בתחום הציור והאיור, ובזמנו החופשי נהג להעתיק תמונות של ציירים מפורסמים. בגיל 16 החל בלימודי משפטים, אך בה בעת גילה עניין רב במתמטיקה ובמדעים. כתוצאה מכך ולמרות התנגדותו אביו (שיעד לו קריירת פקיד ממשלתי) החליט הויגנס כי ברצונו להקדיש את חייו לתחום המחקר המדעי.
בשנת 1645–1647 למד הויגנס באוניברסיטת ליידן לפי החלטת אביו. החל בשנת 1646 היה פראנס ואן סחוטן למדריך פרטי להויגנס ולאחיו הגדול קונסטנטין, בעקבות המלצת דקארט. ואן סחוטן עדכן את ידיעותיו המתמטיות, ובעיקר חשף אותו לשיטות דיפרנציאליות השימושיות בגאומטריה, שפותחו אותן השנים ומעט קודם לכן בעיקר על ידי פרמה.
במרץ 1647 עבר לקולג' אורנג' החדש בברדה, עיר בה שירת אביו כאוצר. המעבר נכפה עליו לאחר שאחיו לודוויק ערך דו-קרב עם סטודנט. באמצעות מעורבותו הענפה במוסד החדש, דאג האב להמשך לימודיהם (הקולג' נסגר ב-1669). רקטור הקולג' היה התאולוג ההוגנוטי אנדרה ריבה. כריסטיאן התגורר בביתו של המשפטן יוהאן הנריק דאובר, ולמד מתמטיקה מג'ון פל. הוא סיים את למודיו בשנת 1649 ולאחר מכן שירת תקופה כדיפלומט יחד עם דוכס נאסאו[1] לואי הנרי. כחלק ממשרתו שירת בבנטהיים ולאחר מכן בפלנסבורג. לאחר שסיים את שירותו זה ביקר בקופנהגן ובהלסינייר, הוא קיווה לחצות את הארסונד ולפגוש את דקארט בסטוקהולם, תקווה שלא צלחה.
התכתבות מוקדמת[עריכת קוד מקור | עריכה]
הויגנס כתב בדרך כלל בצרפתית או בלטינית (באותם ימים השפה המקובלת בהגות ובמדע). עוד בשנותיו כסטודנט באוניברסיטת ליידן החל בהתכתבות עם המתמטיקאי מארה מרסן, שמת זמן קצר לאחר מכן, ב-1648. מרסן כתב לאביו של הויגנס על כישרונו של בנו, כריסטיאן, למתמטיקה, ואף החמיא לו ” אם ימשיך כך יתעלה על ארכימדס עצמו”[2]. במכתבים אלו מתבררים מוקדי העניין המוקדמים של הויגנס במתמטיקה. באוקטובר 1646 מופיע הנושא גשר תלוי, וההדגמה שקו השרשרת אינו פרבולה כפי שסבר גליליי, זאת כאשר פרסום ההוכחה הפורמלית של יואכים יונגיוס(אנ') איחר להתפרסם אחרי מות יונגיוס, רק ב-1669. לימים ניסח הויגנס את מהות העקומה במקביל ליוהאן ברנולי וללייבניץ. בשנים 1647–1648 עולים הניסיון הכושל של סן ואנסון(אנ') לתרבע המעגל, חישוב אורך של אליפסות ועקומות, ותיאור תנודות "מיתר רוטט". כמה מתחומי העניין של מרסן בתקופה זו, כמו הציקלואיד (הוא שלח את חיבורו של אוונג'ליסטה טוריצ'לי על העקום), מרכז הקשה, וקבוע הכבידה, הם נושאים שהויגנס לקח ברצינות רק לקראת סוף המאה ה-17.
מרסן עסק גם בתורת המוזיקה, וכן כתב בנושא להויגנס, שציין את העדפתו לכוונון הלא-מושווה "מינטון" (עד המאה ה-19 לא היו אמצעים להשגת כוונון מושווה) וכן פיתח באופן עצמאי את הכוונון המוכר בשם "31 כוונון מושווה" (אנ'), והראה באמצעות לוגריתמים (נוסחו כ-50 שנים קודם לכן על ידי ג'ון נפייר) הקרבה של כוונון זה לכוונוני מינטון המקובלים באותה תקופה. ייתכן ואף סביר שהויגנס נדרש למחקר המוזיקלי בעקבות עיסוקו של אביו בהלחנה כמו גם המסורת הענפה בתחום בארצות השפלה אותן שנים.
בכורה מדעית ופרסומים מוקדמים[עריכת קוד מקור | עריכה]

הויגנס פרסם בזהירות את הממצאים והעבודות שלו, גם בהשפעת מורו ואן סחוטן שחשש למוניטין האישי שלו. פרסום הבכורה שלו ב-1651 היה בגאומטריה (עד המאה ה-18 גאומטריה הייתה הענף המתמטי המקובל והממוסד היחידי) "תרבוע גופי סיבוב"[3]. היא כללה ממצאים ופיתוחים עוד מההתכתבותו עם מרסן בשנים קודם לכן, למשל הכשל הלוגי בתרבוע המעגל של סן ואנסון. השיטות המועדפות עליו היו אלו של ארכימדס ופרמה. בעיות תרבוע היו סוגיה מרכזית בשנות ה-50 של המאה ה-17, ובתיווך קלוד מילון(אנ'), עורב הויגנס בדיון על המתמטיקה של תומאס הובס, בו הצביע בהתמדה על הטעויות בעבודתו של הובס וכך קנה לו מוניטין בינלאומי.
בשנים 1652 – 1653 עסק במחקר תאורטי של עדשות כדוריות, אך לא פרסם ממצאיו, שמקבילים להם פרסם אייזק בארו ב-1669 באופן עצמאי. המניע המרכזי של הויגנס היה הבנת עקרונות הפעולה של הטלסקופ. ב-1655 החל ללטש עדשות יחד עם אחיו קונסטנטין. ב-1662 תכנן את מה שמכונה בימינו, על שמו, עינית הויגנס בת שתי העדשות. ייצור עדשות היה מוקד עניין משותף, דרכו התאפשר להויגנס לפגוש את ברוך שפינוזה (ליטש עדשות לפרנסתו), אשר אחז בהשקפות שונות על המדע, והיה מחויב יותר להשקפת העולם הקרטזית. באופן דומה, בעקבות העיסוק המשותף בליטוש עדשות, התוודע הויגנס לעבודתו של אנטוני ואן לוונהוק ממציא המיקרוסקופ, ועורר את עניינו של אביו בעולם המיקרוסקופי.
ב-1657, בעקבות התוודעותו לעיסוקם של פרמה, פסקל, ודסארג במשחקי מזל, פרסם את החיבור השיטתי הראשון בתורת ההסתברות, "היקש במשחקי מזל"[4]. מורו לשעבר, ואן סחוטן, תרגם את החיבור המקורי של הויגנס מהולנדית ללטינית ופרסם אותו בספרו "תרגילים מתמטיים"[5]. החיבור עוסק במשחקי מזל, ומתמקד במיוחד בבעיית הניקוד. הויגנס התבסס על המושגים האינטואיטיביים "משחק הוגן" ו-"חוזה שוויוני", ונעזר בהם כדי לנסח תאוריה של ערכי תוחלת. ב-1662 שלח רוברט מארי(אנ') להויגנס את רשימותיו של ג'ון גראונט על תוחלת החיים של אוכלוסיות, ובעקבות כך הויגנס ואחיו הצעיר לודוויק עבדו על התאוריה של תוחלת חיים. בכך היו שניים לעסוק באקטואריה רק לגראונט עצמו.
ב-3 במאי 1661, יום הכתרתו של צ'ארלס השני, ובמהלך שהותו של הויגנס בלונדון, צפה במעבר של כוכב הלכת חמה על פני השמש, בעזרת הטלסקופ מתוצרתו של ריצ'רד רייב (שעבד בין היתר עם רוברט הוק וכריסטופר רן), יחד עם האסטרונום תומאס סטריט ורייב. לימים תצפית זו עוררה מחלוקת, עם פרסמו של יוהנס הווליוס איור מפורט של המעבר כתב לו הנרי אולדנבורג, ממיסדי החברה המלכותית, כי תומאס סטריט טוען לאי התאמה בין התיעוד ותצפיתם. כך החלה התכתבות של הויגנס עם הווליוס, בה העביר לו כתב יד של ג'רמיה הורוקס על מעבר נוגה על פני השמש ב-1639.
באותה שנה, הויגנס, שעסק בעבר בתורת המוזיקה, בין היתר בהתכתבות עם מרסן, היה בעל השכלה מוזיקלית וניגן בצ'מבלו, שב לעסוק בתורת המוזיקה ובפרט בתאוריות של סימון סטייפין(אנ'). הוא גילה מעט רצון לפרסם את התאוריות שלו על זכות וצרימה, אשר כמה מהן נותרו אבודות במשך מאות שנים. תצוין הקרבה בין התחום המוזיקלי לענף הפיזקלי בחקר גלים ותנועה הרמונית.
ב-1663 נבחר לכהן כחבר זר בַּחברה המלכותית.
בצרפת[עריכת קוד מקור | עריכה]
הויגנס היה דמות מוכרת במה שכונה "האקדמיה של מונמור", חוג פורה של הוגים ומדענים. במחלוקת שהביאה להפסקת פעילות הסלון תמך בסיעה "הפורשת" שראתה ההבטחה שבתכנון וביצוע ניסויים על פני דיונים תאורטיים מוגבלים בשל היעדר הגבולות שבהם ובהיעדר נקודת משען לבד מטיעון הקוגיטו. במהלך 1663 בביקורו השלישי בפריז עם תום פעילות הסלון, ניצל הויגנס ההזדמנות כדי לצדד בפעולה מבית מדרשו האמפריציסטי של פרנסיס בייקון כעתיד למדע. ב-1666 היגר לפריז וזכה למשרה באקדמיה הצרפתית למדעים שרק נוסדה בחסות לואי ה-14.
בפריז הויגנס מצא לו פטרון ומכותב, ז'אן בטיסט קולבר. יחסיו עם חברי האקדמיה האחרים לא היו טובים, וב-1670, בעודו חולה מאוד, הוא פנה לפרנסיס וורנון כאחראי למימוש צוואתו, ובה מסירת חזקה על מאמריו לַחברה המלכותית עם מותו. אולם, זמן קצר לאחר מכן, פרצה מלחמת הולנד–צרפת, וככל הנראה בשל תמיכתה של אנגליה בצרפת, הופסקו קשרי החברה המלכותית עמו, כנראה לפי החלטתו של נשיאה רוברט הוק.
דניס פפין, לימים ממציא מנוע הקיטור היה עוזרו של הויגנס ב-1671. באחד הניסויים שלהם, אשר לא הניב פירות באופן ישיר, עמד פיתוחו של מנוע בעירה פנימית המתודלק באבק שרפה. ב-1678 עבר פפין לאנגליה והמשיך את מחקרו בתחום.
במצפה הכוכבים בפריז, שבנייתו הושלמה ב-1672, המשיך הויגנס לערך תצפיות אסטרונומיות. ב-1678 הציג הויגנס את עוזרו החדש בפני ניקולא מלבראנש, ג'ובאני קאסיני ומדענים והוגים נוספים, המתמטיקאי והפיזיקאי בן ארצו, ניקולאס הרטסוקר, והציגו מיקרוסקופ פרי פיתוחו של הרטסוקר. לימים נתגלעו היחסים בין השנים כאשר למורת רוחו של הרטסוקר, במאמרים שפרסם בסמוך הויגנס השמיט את שמו.
זה היה בפריז, גם, שהויגנס פגש את הדיפלומט הצעיר גוטפריד לייבניץ, ב-1672. באותה שנה לייבניץ עמל על בניית מכונת החישוב שלו, ועבר להתגורר בלונדון בתחילת 1673 יחד עם דיפלומטים ממיינץ. במרץ 1673, עם שובו של לייבניץ לפריז, החל ללמוד מתמטיקה בהוראת הויגנס. התכתבות ענפה התפתחה בין השניים, ובה בין היתר הויגנס גילה חוסר רצון לקבל את יתרונות השיטות בחשבון אינפיניטסימלי שפיתח לייבניץ, שהן למעשה הכללות של שיטות גאומטריות, דוגמת התרבוע, שפותחו עוד על ידי ארכימדס ושוכללו במאה ה-17 בין היתר על ידי הויגנס עצמו.
אחרית ימיו[עריכת קוד מקור | עריכה]

ב-1681 שב הויגנס להאג עם שקיעתו בדיכאון חמור. ב-1684 פרסם את חיבורו[6] על המצאתו שלו ושל אחיו "טלסקופ נטול שפופרת". ככל הנראה ברוח הפיתוח היו גם רעיונותיו של ניקולאס הרטסוקר, עוזרו לשעבר של הויגנס.
ב-12 ביוני 1689, במהלך ביקורו השלישי באנגליה, פגש את אייזק ניוטון. הם שוחחו על פצלת איסלנדית, והמשיכו בהתכתבות על כוח גרר.
במכתב מ-1693 לפיליפ דה לה איר(אנ') תיאר הויגנס מופע טבעי של התופעה האקוסטית הידועה כיום בשם פלאנג'ינג[7].
הוא נפטר בהאג ב-8 ביולי 1695, ונקבר בגרוטה קרק. את עיזבונו הרוחני הוריש לאוניברסיטת ליידן[8].
הויגנס מעולם לא נישא, לא ידוע על קשרים שקיים עם נשים.
עבודתו כמדען[עריכת קוד מקור | עריכה]
הויגנס מוערך כפילוסוף של הטבע המוביל באירופה בתקופה שבין דקארט לניוטון, 1650 עד בערך 1672. הוא מיקד את פועלו במה שהוגדר כחללים שהפילוסופיה המכניסטית טרם הצליחה להסביר, ובאופן ספציפי חיפש הסבר לפעולת כח הכבידה שלא כלל את מושג הפעולה מרחוק, לשיטתו של הויגנס הסבר משמעו ניסוי.
חוקי התנועה, התנגשויות והכבידה[עריכת קוד מקור | עריכה]
הגישה המקובלת של ה"פילוסופים המכניסטים" (למעשה אבות הפיזיקה) הייתה להגות תאוריות המתבססות על מושג ה-"פעולה דרך מגע". הויגנס אימץ גישה זאת, לא מבלי לראות את הקשיים המושגיים שהיא מעוררת ואת נקודות התורפה שלה. לעומתו, לייבניץ, שהיה תלמידו בתקופת שהותו בפריז, נטש גישה זו. הנחת מוצא זו של "פעולה דרך מגע" הפכה את "תאוריית ההתנגשויות" למרכזית בפיזיקה כמו גם את הפילוסופיה האטומיסטית. לתפיסתו של הויגנס על הדרישות מהפילוסופיה המכנית להיות קפדניות ככל תחום פילוספי אחר. חומר בתנועה יצר את היקום, ולכן רק הסברים במונחים מסוג זה, כלומר חומר ותנועה, יהיו ברי הבנה. כמרבית ההוגים והמדענים הושפע מהגישה הקרטזית, אך לא היה מחסידיה האדוקים, דוגמת שפינוזה. הוא חקר התנגשויות אלסטיות בשנות ה-50 של המאה ה-17 אך השהה את פרסום התוצאות אליהן הגיע משך יותר מעשור.

כמו חוקרים אחרים, הסיק הויגנס שחוקי דקארט לתיאור התנגשויות אלסטיות של שני גופים שגויים, וניסח חוקים מתוקנים, נכונים הנדסית. צעד חשוב לקראת ניסוח החוקים שלו היה קבלת תוקפו של עקרון היחסות של גלילאו בתיאור התנגשויות. במהלך שנים הפיץ את ממצאיו באופן אישי לאישים דוגמת כריסטופר רן, ויליאם ברונקר, אך גם בשל מלחמות הולנד-אנגליה, קשריו עם החברה המלכותית נקטעו לפרקים, ומהתכתבות מזכיר החברה המלכותית, הנרי אולדנבורג ושפינוזה מתבהר כמה מעט היה ידוע על התקדמות הויגנס בתחום. לבסוף נתקבעו ממצאיו סופית עם ההוצאה לאור של הפרינקיפיה מאת ניוטון ב-1684, ממצאים אליהם הגיע ניוטון באופן עצמאי.
בספרו "מדע המכניקה" מציין מאך כי הויגנס ניסח בעבודותיו את החוק השני של ניוטון ואף נוסח מסובך ופחות כללי לחוק התנועה השלישי[9]. ב-1659 כימת את הכוח הצנטריפטלי (מכפלה של נגזרת ההעתק), הפועל על גוף הנע בתנועה מעגלית. בסימון מודרני, הנוסחה של הויגנס היא:
כאשר m הוא מסת העצם, v המהירות ו-r הרדיוס. הויגנס חקר את טבעו של הכוח הצנטריפוגלי, והדגים את קווי הדמיון בין כוח זה לכוח הכבידה (ראו גם עקרון השקילות).
הגישה של הויגנס החמיצה מספר מושגים מרכזיים בפיזיקה מתמטית, אך הוליכה להתקדמויות משמעותיות רבות בידי אחרים. עבודתו על מטוטלות הייתה המתקדמת מסוגה לתיאור תנועה הרמונית פשוטה, אך הנושא תואר בשלמותו מאוחר יותר בפרינקיפיה מאת ניוטון. ב-1678 לייבניץ ניסח על בסיס עבודתו של הויגנס על התנגשויות את הרעיון של חוק שימור, שהויגנס הותיר בלתי מפורש, והגה את רעיון "כוח החי"[10] שבמהרה היה למקובל בחישובים הנדסיים אף שלא היה חלק מהמכניקה הניוטונית הפורמלית שנוסחה על יסוד חוק שימור התנע ולא מכירה במושג האנרגיה ובשימורה המתגלם בניסוח "כוח החי".
סטטיקה והידרוסטטיקה[עריכת קוד מקור | עריכה]
הויגנס תרם תרומה משמעותית בפיתוח כלים אנליטיים חדשים וביישום פיזיקלי של כלים אלו, לעיתים קרובות תוך יישום מוקדם של שיטות שכיום הן חלק מהחשבון האינפיניטסימלי (בעיקר בהשפעת פרמה) ושבימיו היו בגדר חידושים גאומטריים וראשית מיסודן של שיטות אלגבריות. בעשותו כן, הוא תרם לענפי המכניקה המתהווים של הסטטיקה וההידרוסטטיקה. הוא היה בין הפותרים של סדרת בעיות מתמטיות-פיזיקליות שהוצגו כאתגר עבור המתמטיקאים באירופה של שלהי המאה ה-17 (בעיות שחלקן הוצגו על ידי גלילאו גליליי בעבודותיו המכוננות של הפיזיקה), כדוגמת בעיית קו השרשרת - המבקשת למצוא את משוואת העקום המתאר כבל התלוי בין שני עמודים.
כפי שצוין בפרק על המכניקה של הויגנס, תפיסתו של הויגנס המכניקה כולה הייתה למעשה תפיסה סטטית מצומצמת, הוא שלל מכל וכל עקרון פעולה מרחוק.
כשניגש לבעיית קו השרשרת, ולבעיות בסטטיקה ובהידרוסטטיקה בכלל, הויגנס הניח כאקסיומה שמערכת מכנית נמצאת בשיווי משקל אם מרכז הכובד שלה הוא במיקום הנמוך ביותר האפשרי תחת האילוצים של הבעיה. זוהי דוגמה לניסוח סוגיה פיזיקלית כבעיית קיצון מתמטית (ראו גם משפט פרמה). בגישה זו נקט גם בחיבורו המרכזי על הידרוסטטיקה, "על הגופים הצפים"[11], שכתב בגיל 21 ולא טרח לפרסמו[12], וזאת כדי לגזור את חוק ארכימדס על ציפה. חיבורו זה על הידרוסטטיקה דומה מאוד באופיו לעל גופים צפים של ארכימדס ומשחזר חלק מהתוצאות שלו. החיבור מעיד על הבנה מעמיקה של הויגנס את ממצאיו של ארכימדס ואת היישום הכמותי (מרובה בדוגמאות לחישוב מרכז כובד), ומתעד ניסויים בציפה ואיזון שערך בעצמו, תוצאות מקוריות והרחבה של עבודתו של ארכימדס. אף על פי שבכתיבת חיבור זה הויגנס הפך למדען הראשון שהתקדם מעבר למחקריו ההידרוסטטיים של ארכימדס, הויגנס עצמו לא העריך את החיבור כבעל חשיבות או תועלת רבה[13].
אופטיקה[עריכת קוד מקור | עריכה]
אופטיקה גאומטרית; טכניקות אופטיות[עריכת קוד מקור | עריכה]

בשנת 1653 העלה על הכתב את ידיעותיו וניסיונו באופטיקה גאומטרית, ב"דיון על החזרה וטלסקופיה"[14]. בכתב יד זה, שפורסם רק לאחר מותו ב-1703[15] כינס את ידיעותיו על חוק השבירה, על מציאת מוקדי העדשה ומקדמי השבירה שלה, על מבנה העין, על תאוריית ההגדלה של עדשות, ועל בניית טלסקופים. אף על פי שעיקר המאמר הוא שיחזור תוצאותיהם של קודמיו וחוקרים בני זמנו, בעיקר של תוצאותיו של קפלר ב"דַיוֹפְטְריס"[16] שראה אור ב-1611 והיה חלק מספרי הלימוד של שטאמפיון (מורו של הויגנס), התייחדה עבודתו של הויגנס בדיוק על פני קירובים בלבד שהציעו קודמיו[17]. באמצעים חישוביים תכנן ובנה את הרכיב האופטי המוכר כיום כעינית הויגנס, שהייתה לעינית הראשונה שהורכבה משתי עדשות. הוא החל לחקור את האברציה הכדורית ב-1665, וגזר עבור עדשות עם מפתח[דרושה הבהרה] ואורך מוקד מסוימים את הצורה אשר תביא לעיוות כדורי מינימלי בעבור שטף קרניים מקבילות. הוא חקר גם את הקשר בין ההגדלה, הבהירות והרזולוציה (חדות) בעבור טלסקופים באורך נתון.
הויגנס רכש מיומנות טכנית גבוהה יחד עם אחיו ביצור ובפרט בליטוש עדשות כדוריות. העדשות שייצרו החל משנת 1655 היו מאיכות מעולה, כך שהטלסקופים תוצרת האחים הויגנס היו הטובים ביותר בזמנם. ב-1685 הויגנס סיכם את הידע הטכני שלו בנוגע לייצור עדשות בחיבורו "אודות ייצור וליטוש עדשות טלסקופ"[18]. בחיבורו "תצפית שמימית מוקטנת"[19] הוא תיאר סוג חדש של טלסקופ חסר צינור, הנקרא "טלסקופ אווירי"(אנ') שהמצאתו לעיתים מיוחסת גם לאדריאן אוֹזוּט(אנ').
התאוריה הגלית של האור[עריכת קוד מקור | עריכה]
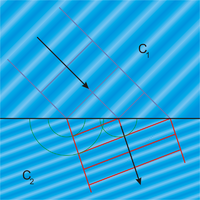
הויגנס זכור במיוחד בשל התאוריה הגלית שלו על טבע האור, אותה הציג לראשונה ב-1678 בפני האקדמיה הצרפתית למדעים. היא פורסמה לראשונה ב-1690 בחיבורו Traité de la lumière (חיבור על אור), והפכה לתאוריה המתמטית הראשונה של האור.
עיקרון יסודי של התאוריה של הויגנס הוא שמהירות האור סופית, עובדה שהייתה מושא להדגמה ניסויית בידי אולה רמר (ב-1679 במצפה הכוכבים של פריז), אך שסוברים שהויגנס כבר האמין בה עוד לפני כן. התאוריה של הויגנס היא קינמטית באופייה וההיקף שלה מוגבל בעיקר לאופטיקה גאומטרית. היא מכסה מעט מהתחום שכעת ידוע כאופטיקה פיזיקלית. היא עוסקת בחזיתות גלים והקרניים הישרות המייצגות אותן, כאשר התקדמות הגל מתוארת באמצעות גלים כדוריים הנפלטים מחזית הגל (ראו גם עקרון הויגנס-פרנל). היא הוצדקה כתאוריה אתרית, המערבת העברת גלים באמצעות חלקיקים אלסטיים לחלוטין, בהתאם להשקפתו של דקארט. טבע האור היה לפיכך זהה לזה של גל אורכי.
הויגנס ערך כבר ב-1672 ניסויים הקשורים לתופעת השבירה הכפולה בגבישי קלציט, תופעה שתוארה בספרות המדעית ב-1669 על ידי ראסמוס ברתולין. במבט ראשון הוא לא היה יכול להסביר את הממצאים. מאוחר יותר הוא הסביר את התופעה בעזרת התאוריה שלו של חזיתות גלים ומושג האוולוטים. הויגנס גזר נוסחאות המתארות את התופעה, ותיאר באופן מבריק את התנהגות הקרן הבלתי רגילה באמצעות בנייה גאומטרית מפורסמת[20] של המעטפת של גלים אליפסואידים הנפלטים מפני הגביש. הוא גם פיתח רעיונות על קאוסטיקות. ניוטון בספרו אופטיקה (Opticks) ב-1704 הציע במקום זאת תאוריה חלקיקית של האור. התאוריה של הויגנס לא נתקבלה על ידי מספר מדענים, בעיקר מכיוון משום שגלים אורכיים לא יכולים להפגין שבירה כפולה. תבניות ההתאבכות של תומאס יאנג אשררו את נכונותה של התאוריה הגלית; תוצאות הניסויים לא היו ניתנות להסבר באמצעות חלקיקי אור. הפתרון לבעיה שניצבה במקור בפני הויגנס היה שהאור הוא גל רוחבי. כדי לקרוא על נקודת המבט הפיזיקלית המודרנית ראו דואליות גל חלקיק.
הויגנס חקר גם את השימוש של עדשות במקרנים. נזקף לזכותו הקרדיט על המצאת פנס הקסם, שתואר על ידו בהתכתבות ב-1659. גם למדענים אחרים מהתקופה נזקף הקרדיט על המצאת פנס כזה; לב המחלוקת הוא מי השתמש לראשונה בעדשות לצורך הקרנה טובה יותר.
גילויים אופטיים חשובים נוספים של הויגנס הם הסברו החדשני לתופעת ההילה, וההבחנה הראשונית של תכונת קיטוב האור - ב-1690 הויגנס ערך[21] ניסוי בו פיצל אור שמש לשתי קרניים (באמצעות העברתו דרך גביש שבירה כפולה), ולאחר מכן העביר את כל אחת מהקרניים דרך גביש קלציט נוסף. הויגנס גילה שאם מציבים את הגביש השני בזווית נכונה, כל אחת מהקרניים שנוצרו במעבר בגביש הראשון עשויה להיעלם לגמרי. הויגנס הדגים שאם מסובבים את הגביש השני סביב כיוון הקרן העוברת דרכו, קיימת זווית מסוימת בו מידת העברת הקרן בתוך הגביש מתאפסת לגמרי. הויגנס הסביר את הממצאים בכך שגביש השבירה הכפולה "מפצל" את אור השמש לשתי קרניים בעלי תכונות שונות זו מזו (במינוח מודרני: בעלות קיטובים ניצבים) ושונות באופן מהותי מאור השמש הרגיל (אור לא מקוטב).
מנוע הויגנס[עריכת קוד מקור | עריכה]
הויגנס הגה ותכנן, ביחד עם דניס פפין (הידוע כממציא מנוע הקיטור), סוג של מנוע בעירה פנימית העובד על בסיס אבק שרפה. הפרויקט הזה של מנוע אבק שרפה (gunpowder engine) לא הניב פירות באופן ישיר, אך כמה מהעקרונות שהופיעו בהתכתבות שלהם מצאו את דרכם לבניית מנוע הקיטור.
הורולוגיה[עריכת קוד מקור | עריכה]
הויגנס תכנן שעונים מדויקים יותר מאלו שהיו קיימים בתקופתו. ההמצאה שלו את שעון המטוטלת הייתה פריצת דרך בבקרת זמן, והוא הכין אב-טיפוס שלו בסוף 1656. עוד לפני כן, הוכיח הויגנס כי זמן המחזור של מטוטלת תלוי רק באורכה, ובעקבות כך הדרך להמצאתו של שעון המטוטלת, המדויק בהרבה משאר שעוני התקופה, הייתה קצרה. השעון החדש היה מתאים פוטנציאלית לשימוש לצורכי ניווט (מציאת קו אורך לפי כרונומטר). ניצול ההמצאה לניווט ימי היה מאוד בעייתי, עם זאת.
מטוטלות[עריכת קוד מקור | עריכה]

ב-1673 הויגנס פרסם את Horologium Oscillatorium sive de motu pendulorum, עבודתו המרכזית על מטוטלות והורולוגיה, ואחד החיבורים החשובים על מכניקה שנכתבו במאה ה-17. לפני פרסום העבודה, נצפתה על ידי מרסן ואחרים התכונה שמטוטלות הן לא לגמרי איזוכרוניות; זמני המחזור שלהם תלויים במשרעת התנודה, כאשר תנודות רחבות יותר לוקחות יותר זמן מתנודות צרות יותר.
הויגנס ניתח את הבעיה הזאת באמצעות מציאת העקום אשר משקולת תחליק במורדו באותה כמות זמן, ללא קשר לנקודת ההתחלה שלה; בעיה זו נקראת בעיית הטאוטוכרון. באמצעות שיטות גאומטריות שהיוו למעשה שימוש מוקדם בשיטות החשבון האינפיניטסימלי, הוא הראה שעקום זה הוא ציקלואיד, במקום הקשת המעגלית של קצה המטוטלת, ולפיכך שמטוטלות הן לא איזוכרוניות. ב-Horologium Oscillatorium הויגנס עוסק גם בתאוריה המתמטית של אוולוטים, וזה בנוסף על פתרון בעיית הטאוטוכרון, הויגנס הוכיח שהאוולוט של עקום הציקלואידה הוא בעצמו ציקלואידה (שני חצאי ציקלואידה), עובדה שאיפשרה לו לבנות שעון מטוטלת איזוכרוני (שנקרא מטוטלת ציקלואידית).

בספרו זה, הוא גם פתר את הבעיה הבאה שהוצעה על ידי מרסן: איך לחשב את זמן המחזור של מטוטלת קשיחה שצורתה שרירותית. הפתרון לבעיה היה כרוך בגילוי מרכז התנודה (center of oscillation) ואת הקשר ההפוך שלו עם מיקום נקודת התמיכה. באותה עבודה, הוא ניתח את המטוטלת הקונית, המורכבת ממשקולת על מיתר שמתווה חרוט במרחב, וזאת באמצעות מושג הכוח הצנטריפוגלי. הויגנס היה הראשון שגזר את הנוסחה לזמן המחזור של מטוטלת מתמטית אידיאלית (עם מוט חסר מסה ואורך שגדול בהרבה מהמשרעת של התנודה), ובסימון מודרני:
כאשר T הוא זמן המחזור, l הוא אורך המטוטלת ו-g היא תאוצת הכובד. בעבודתו על זמן המחזור של מטוטלות מורכבות הוא עשה תרומות מכרעות להעלאת מושג מומנט האינרציה.
בין גילוייו היותר מעמיקים בתחום תורת התנודות נמנית הבחנה חשובה אליה הגיע בזמן שצפה בתנודות מצומדות: שניים משעוני המטוטלת שלו שהוצבו על אותה משענת (מעיין חוט אופקי מתוח) נטו להסתנכרן זה עם זה, ולנוע בכיוונים הפוכים (כלומר עם אותו זמן מחזור ובהפרש פאזה של 180 מעלות). הוא דיווח על התוצאות דרך מכתב לחברה המלכותית, שם החלו להשתמש במונח "צורה מוזרה של סימפתיה" לתיאור התופעה. המושג ידוע כעת בשם entrainment.
שעון "גלגל איזון קפיצי"[עריכת קוד מקור | עריכה]
הויגנס פיתח שעון בו גלגל האיזון(אנ') הוא קפיץ פיתול, בערך באותה תקופה, ובאופן בלתי תלוי ברוברט הוק. הרעיון החלוצי של הויגנס היה לרתום את תופעת התהודה לשימוש מעשי, ולהוסיף לגלגל האיזון, קפיץ אשר יגרום לו להתנודד בתדירות התהודה הטבעית של המערכת, כך שיבקר את מהירות סיבוב גלגלי השעון ויאפשר להם לשמור על קצב סיבוב אחיד. המחלוקת על שאלת קדימות ההמצאה נמשכה מאות שנים. הדגם של הויגנס נעזר בקפיץ איזון ספירלי; הוא נעזר בסוג זה של קפיץ כי מנגנון האיזון בשעון הראשון שלו השלים יותר מסיבוב וחצי. מאוחר יותר השתמש בקפיצים כאלו בשעונים קונבנציונליים יותר, שנבנו למענו על ידי משפחת טוראה[22] בפריז בסביבות 1675.
קפיצים מסוג זה הפכו לרכיבי מפתח בשעונים מכניים מודרניים עם תמסורת מנוף נתיקה כיוון שהם איזוכרוניים יותר. שעונים קודם להוק ולהויגנס, לעומת זאת, השתמשו במנגנון תמסורת של "כננת כתר" או "מחגר משונן"[23] (אנ').
בשנת 1675 רשם הויגנס פטנט על רכיב בשעוני כיס. שעונים אלו יוצרו בפריז החל מ-1675 על ידי משפחת טוראה. מרשמיו עולה כי ככל הנראה, הויגנס ביקש להחליף את גלגלת ה"פוזאה"(אנ') בשעונים בקפיץ פיתול וכך לתזמן באופן שווה (איזוכרוני) את גלגל האיזון, באותו האופן סבר שמתלה בצורת ציקלואידה יהפוך את שעון המטוטלת לאיזוכרוני.
אסטרונומיה[עריכת קוד מקור | עריכה]
הטבעות של שבתאי וירחו טיטאן[עריכת קוד מקור | עריכה]

ב-1655, הויגנס הציע כי שבתאי היה מוקף בטבעת מוצקה, אותה תיאר כ-"טבעת דקה, שטוחה, שאינה נושקת בשום מקום, ונטויה ביחס למישור המילקה". שנה מאוחר יותר, ב-1656, גילה כי הטבעות סביב שבתאי מורכבות מסלעים. באמצעות טלסקופ שבירה עם כוח הגדלה של פי 50 שתכנן בעצמו, הויגנס גם גילה את הראשון מבין הירחים של שבתאי, טיטאן. באותה שנה הוא צפה ושרטט באופן סכמטי את ערפילית אוריון. התרשים שלו, הראשון שידוע של ערפילית אוריון, פורסם בחיבורו Systema Saturnium מ-1659. באמצעות הטלסקופ המודרני שלו הוא הצליח לחלק את הערפילית לכוכבים שונים. החלק הפנימי הבוהק יותר ידוע כעת כאזור ההויגני, בהוקרה לתרומתו. הוא גם גילה מספר ערפיליות בין כוכביות ומספר כוכבים כפולים.
מאדים וכתם Syrtis[עריכת קוד מקור | עריכה]
ב-1659, הויגנס היה הראשון לתעד בדייקנות את תוואי השטח של כוכב אחר, כשגילה את Syrtis Major, מישור וולקני על מאדים. הוא השתמש בתצפיות חוזרות על תנועת האזור הזה במהלך מספר ימים כדי להעריך את אורך היממה על מאדים, אותו חישב באופן מדויק למדי כ-24.5 שעות. ערך זה סוטה רק מספר דקות מהערך המודרני שלו, שהוא כ-24 שעות ו-37 דקות.
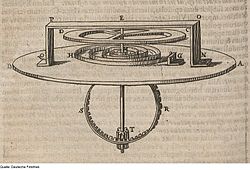
הפלנטריום של הויגנס[עריכת קוד מקור | עריכה]
בהקשר של עבודתו האסטרונומית, ב-1680 הויגנס החל לפתח פלנטריום מכני בעבור האקדמיה המלכותית למדעים. מעבר לתרומה שלו לבניית מנגנונים מכניים המדמים את תנועת גרמי השמיים, הפלנטריום של הויגנס חשוב כי כדי לבנות אותו הויגנס השתמש[24] בכלי מתמטי שלפני כן נחשב לנחלת המתמטיקה הטהורה בלבד - שברים משולבים. את הקישור המעניין שעשה הוא פרסם במאמר שעסק בשיטות לשימוש בהתכנסות של שברים משולבים כדי למצוא את הקירובים הרציונליים הטובים ביותר ליחסי גלגלי שיניים (gear ratios). קירובים אלה אפשרו לו להעריך את מספר השיניים שצריכים להיות על כל גלגל.
קוסמותאורוס[עריכת קוד מקור | עריכה]
זמן קצר לפני מותו ב-1695, הויגנס השלים את כתיבת ספרו Cosmotheoros, שפורסם לאחר מותו ב-1698. בספר זה הויגנס העלה את האפשרות של קיום חיים מחוץ לכדור הארץ על פלנטות, והחשיב זאת לסביר שהם יהיו דומים מאוד לאלו שעל כדור הארץ. ספקולציות כאלו לא היו בלתי נפוצות באותה תקופה, שכן הייתה להן הצדקה איתנה בהשקפת העולם הקופרניקאית ועקרון השפע, אולם הויגנס העמיק יותר בכניסתו לפרטים.
הויגנס כתב שהזמינות של מים במצב צבירה נוזלי היא הכרחית לקיומם של חיים ושתכונות המים חייבות להשתנות מפלנטה לפלנטה כדי להתאים לטווח הטמפרטורות המשתנה. הוא החשיב את התצפיות שלו על כתמים כהים ובהירים על פני השטח של מאדים וצדק כעדות לקיומם של מים וקרח על הפלנטות האלה. הוא טען שלקיום חיים חוץ-ארציים אין אשרור ואין הכחשה בתנ"ך, ושאל מדוע האל ברא את הפלנטות האחרות אם לא כדי לשרת תכלית נעלה יותר מאשר רק לשמש מושא לסגידה בקרב תושבי כדור הארץ. הויגנס טען שמבחינה תאולוגית, המרחקים הגדולים שבין הפלנטות מעידים שכשהאל ברא את העולם הוא לא הועיד את הישויות התבוניות על פלנטה אחת לדעת על אלו שבפלנטות אחרות.
בספר זה הויגנס גם פרסם את השיטה שלו להערכת מרחקים בין כוכביים. הוא הכין סדרה של חורים הולכים וקטנים במסך הפונה לעבר השמש, עד אשר העריך באופן גס כי הבהירות של החור (כפי שנצפית מעמדת התצפית שלו) הייתה זהה בקירוב לזה של הכוכב סיריוס. לאחר מכן הוא חישב שהקוטר הזוויתי של החור (כפי שנראה מעמדת התצפית שלו) הוא כ-1/27,664 מהקוטר הזוויתי של השמש (שהוא כחצי מעלה), ועל פי כן מצא שסיריוס מרוחק מכדור הארץ מרחק גדול פי 27,664 ממרחק השמש ממנו על בסיס ההנחה (השגויה) שסיריוס פולט אור באותה מידה כמו השמש. טכניקת חישוב זה מניחה באופן לא מפורש את חוק היפוך הריבוע של הבהירות; כיוון שבהירות החור יחסית לשטח הזוויתי שלו בעיני הצופה (המכתיב כמה אור שמש הוא "אוסף") וזה יחסי לקוטר הזוויתי בריבוע, כלל היפוך ריבוע המרחק קובע ששורש יחס השטחים הזוויתיים של החור והשמש שווה ליחס המרחקים של סיריוס והשמש מכדור הארץ. תחום הפוטומטריה נשאר בוסרי מאוד עד אשר פייר בוגה ויוהאן היינריך למברט המשיכו את פיתוח התחום.
הנצחה[עריכת קוד מקור | עריכה]
את עבודתו של הויגנס הוקירו במגוון דרכים. בין השאר נקראו על שמו:
- מכתש הויגנס על המאדים
- אסטרואיד 2801הויגנס שהתגלה ב-1935
- הר הויגנס על הירח (ההר הכי גבוה, אולם לא הנקודה הכי גבוהה על הירח)
- גשושית המחקר הוגינס שנחתה על טיטאן, ירח של שבתאי
- עקרון הויגנס-פרנל
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- כריסטיאן הויגנס, באתר פרויקט הגנאלוגיה במתמטיקה
- כריסטיאן הויגנס, באתר MacTutor (באנגלית)
- אתר על הויגנס
- ביוגרפיה באתר ה-BBC
- עוד אתר על הויגנס
- אתרים רבים על הויגנס
- כריסטיאן הויגנס, באתר אנציקלופדיה בריטניקה (באנגלית)
- כתבי כריסטיאן הויגנס בפרויקט גוטנברג (באנגלית)
- כריסטיאן הויגנס, באתר "Find a Grave" (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ ראו גם בית נאסאו
- ^ C. D. Andriesse (25 August 2005). Huygens: The Man Behind the Principle. Cambridge University Press. pp. 78.
- ^ Theoremata de quadratura
- ^ De ratiociniis in ludo aleae
- ^ Exercitationum mathematicarum
- ^ Astroscopia Compendiaria מלטינית, אפשר "חיבור קצר על מכשיר תצפית אסטרונומית"
- ^ Frans A Bilsen& R. J. Ritsma, "Repetition Pitch and Its Implication for Hearing Theory", Acta Acustica united with Acustica 22(2),January 1969
- ^ ארכיון הויגנס
- ^ Ernst Mach, The Science of Mechanics (1919), e.g. p.148 & p.199
- ^ לטינית: Vis Viva, ובניסוח המקובל בימינו לעומת המושג המקובל במכניקה ניוטונית, תנע:
- ^ לטינית: De iis quae liquido supernatant
- ^ פורסם במסגרת מחקר היסטורי במאה ה-20
- ^ Nowacki H. (2010) The Heritage of Archimedes in Ship Hydrostatics: 2000 Years from Theories to Applications. In: Paipetis S., Ceccarelli M. (eds) The Genius of Archimedes -- 23 Centuries of Influence on Mathematics, Science and Engineering. History of Mechanism and Machine Science, vol 11. page 240. Springer, Dordrecht
- ^ במספר נוסחים צרפתית :Tractatus de refractione et telescopiis
- ^ Olivier Darrigol, A History of Optics from Greek Antiquity to the Nineteenth Century, OUP Oxford, 2012
- ^ לטינית:Dioptrice
- ^ Fokko Jan Dijksterhuis, Lenses and Waves: Christiaan Huygens and the Mathematical Science of Optics in the Seventeenth Century, Springer Science & Business Media, 2006
- ^ הולנדית ארכאית:Memorien aengaende het slijpen van glasen tot verrekijckers
- ^ מקור בהשפעה לטינית: Astroscopia compendiaria
- ^ Treatise on light[1]
- ^ Polarized Light, Revised and Expanded [2]
- ^ צרפתית: Thuret
- ^ רכיב הדומה למפתח ראצ'ט
- ^ Christiaan Huygens’ Planetarium [3]




