גל עומד

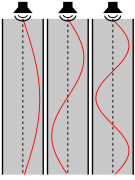
גל עומד הוא מושג פיזיקלי המתאר גל שאינו מתקדם במרחב. המונח נטבע בידי הפיזיקאי הגרמני פרנץ מלדה.
מאפיינים[עריכת קוד מקור | עריכה]

גל עומד הוא צורה רציפה של אופן תנודה. בגל עומד כל האלמנטים המרחביים (מיוצגים על ידי הקואורדינטות x,y,z) מתנודדים באותה תדירות ובאותה פאזה (מגיעים ביחד לנקודת שיווי המשקל), אך לכל אלמנט מרחבי אמפליטודה משלו.
משום שהגל העומד אינו נע במרחב אין לו מהירות חבורה וקצב התנודות שלו מובע על ידי מהירות פאזה.
מבחינה פיזיקלית, גלים עומדים נוצרים על ידי התאבכות: סופרפוזיציה של גלים (נוסעים) וההחזרות שלהם. גל עומד יכול להיווצר כתוצאה משני גלים הנעים בכיוונים הפוכים או כתוצאה מגל המתקדם בתוך תווך שנע לכיוון השני, כפי שיוצג בהמשך.
אופני התנודה של גלים עומדים מייצגים את מצבי התהודה (אופני התנודה העצמיים) של המערכת, כלומר את המצבים שבהם ניתן לעורר את המערכת להיכנס לתנודות בקלות יחסית.
תיאור מתמטי[עריכת קוד מקור | עריכה]
ניתן לתאר גל עומד כהפרעה שבה התלות בזמן "מופרדת" מהתלות במרחב:
כאשר:
- הוא הזמן.
- הוא המקום במרחב.
תיאור מתמטי על ידי גל סינוס[עריכת קוד מקור | עריכה]
במקרים רבים התלות במרחב והתלות בזמן מתוארות על ידי גל סינוסי, למשל:
כאשר:
- - היא המהירות הזוויתית או התדירות הזוויתית - מאחר שבדרך כלל מתארים גלים על ידי פונקציות טריגונומטריות, נהוג לנרמל את התדירות, כך שהארגומנט יהיה כפולה של . לכן , כאשר האות f מייצגת את התדירות. המשמעות של התדירות הופכית לזו של זמן המחזור, ולכן: . כתוצאה מכך אפשר לכתוב את המהירות הזוויתית גם כך:
- - הוא מספר הגל (או וקטור הגל). מספר הגל הוא המקביל המרחבי לתדירות הזוויתית. כשם שהתדירות הזוויתית מתקשרת לזמן המחזור על ידי , מספר הגל מתקשר לאורך הגל על ידי .
- - היא הפרש המופע (פאזה) או זווית המופע. גודל זה מתאר את ההפרש בין הארגומנטים של שני גלים.
גל עומד במיתר[עריכת קוד מקור | עריכה]
גל עומד יכול להיווצר במיתר שבו נעים שני גלים בכיוונים הפוכים. בהקשר הפיזיקלי המונח "מיתר" מתייחס לתווך חד ממדי כלשהו, כמו חוט או חבל. כפי שיוצג בהמשך מאפייניו של הגל העומד מיושמים בין היתר גם בכלי מיתר המשמשים לצורך הפקה של מוזיקה.
- λ=2π/k הוא אורך הגל
התאבכות וסכום אלגברי של גלים מנוגדים[עריכת קוד מקור | עריכה]

גל עומד יכול להיווצר כסכום של שני גלים הנעים בכיוונים מנוגדים, כתוצאה מסופרפוזיציה של שני הגלים.
אלו הן משוואות הגלים של שני גלים הרמוניים הנעים בכיוונים מנוגדים:
כאשר, הסימנים "-" ו- "+" מציינים את כיווני הגלים. מציינים גל סינוס שנע בכיוון ימין של ציר ה- X (הציר האופקי) ב- "-" וגל שנע לכיוון שמאל ב- "+".
הסכום של שני גלים אלו הוא גל עומד:
והוא מתאפס בנקודות x = 0, λ/2, λ, 3λ/2
הסכום של הגלים המנוגדים משקף את התוצרות של ההתאבכות ביניהם.

באיור לעיל מתוארת התאבכות של שני גלים.
- התאבכות בונה (באיור השמאלי) מתרחשת כאשר כל הגלים מגיעים בשיא ומחזקים זה את זה.
- התאבכות הורסת (באיור הימני) מתרחשת כאשר סכום האמפליטודות שווה לאפס. עבור שני גלים, כאשר שני גלים בעלי אותה אמפליטודה מגיעים במופע הפוך (הפרש מופע של חצי מחזור) מתרחשת התאבכות הורסת שכן גל אחד מגיע בשיא והשני בשפל (שיא שלילי).
נקודות צומת וטבור[עריכת קוד מקור | עריכה]

בגל העומד ישנן מספר נקודות בעלות תכונות משותפות:
- נקודות צומת (node) - הן נקודות על המיתר שאינן זזות ולכן נמצאות כל הזמן במנוחה. נקודות אלו נוצרות כתוצאה מכך שסכום הגלים העוברים דרכן תמיד מתאפס.
- נקודות טבור (antinode) - הן הנקודות שבהן מתרחשת התנועה המרבית.
בגל עומד כל הנקודות שאינן נקודות צומת נמצאות בתנועה. תנועה זו מאופיינת במתנד הרמוני. משרעת התנועה של כל נקודה גדלה ככל שהיא רחוקה יותר מנקודת צומת וקרובה יותר לנקודת טבור.
יצירת גל עומד במיתר[עריכת קוד מקור | עריכה]

ישנן מספר דרכים ליצירה של גל עומד במיתר, כתלות במצב של הקצוות.
כאשר שני הקצוות חופשיים, יש ליצור בו זמנית בכל צד של המיתר גל מחזורי שיהיה מנוגד לגל שנוצר בצדו השני.
כאשר אחד הצדדים תפוס, גל מחזורי שנוצר בצדו האחד יוחזר בכיוון הפוך מהצד השני.
ניתן גם ליצור גל עומד במיתר שתפוס בשני קצותיו. על עיקרון זה מתבססים כלי נגינה רבים כפי שיוצג בהמשך. מצב זה הוא שונה מהאחרים, שבהם לפחות אחד מקצוות המיתר חופשי.
אופני התנודה של מיתר התפוס בשני קצותיו[עריכת קוד מקור | עריכה]


כאמור, תנועתו של גל עומד במיתר שתפוס בשני קצותיו שונה מזו של מיתר שבו לפחות אחד הקצוות חופשי. זאת משום שכאשר המיתר תפוס בשני קצותיו כל אחד מהם מהווה נקודת צומת. דבר זה מגביל את אורכי הגל האפשריים עבור הגל העומד.
תדירות הגל של מיתר התפוס בשני קצותיו, עבור כל אחד מאופני התנודה תהיה:
כאשר:
- f - תדירות
- L - אורך המיתר
- n מייצג את אופני התנודה
על פי המשוואה היסודית של הגלים:
כאשר:
- v - מהירות פאזה
- - אורך הגל
ומכאן הקשר בין אורך המיתר לאורכי הגל האפשריים:
כלומר, גל עומד במיתר ייווצר רק עבור גלים שאורך המיתר מהווה כפולה שלמה של מחצית אורך הגל שלהם. כאשר מחצית אורך הגל שווה לאורך המיתר מתקבל אופן התנודה הבסיסי (n=1).
גלים עומדים בכלי נגינה[עריכת קוד מקור | עריכה]
אופן פעולתם של מרבית כלי הנגינה מבוסס על יצירת גלים עומדים באופנים שונים.
במוזיקה, אופני תנודה של כלים רוטטים (כלי מיתר, חלילים וכלי נשיפה, תופים ועוד) נקראות הרמוניות או צלילים עיליים.
מיתר[עריכת קוד מקור | עריכה]

במיתר של כלי מיתר המקובע בשני קצותיו ניתן ליצור גלים עומדים על ידי פריטה. פעולת הפריטה גורמת למיתר להתנודד באחד או יותר מאופני התנודה שלו. ניתן להתייחס לגל עומד במיתר כסכום של שני גלים המתקדמים בכיוונים הפוכים. כשכל אחד מהגלים מגיע לנקודת הקצה הקבועה, הוא מוחזר לאחור, ואם מדובר במעבר מתווך אחד לתווך צפוף יותר, הרי שיתרחש גם היפוך מופע הגל.
צליל המופק מפריטה רגילה של גיטרה מורכב בעיקר מאופן התנודה הבסיסי בתוספת צלילים עיליים חלשים יותר הקרויים גם הרמוניות.
עוגב[עריכת קוד מקור | עריכה]
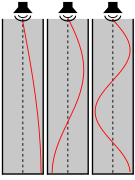
עקרון הפעולה של עוגב שונה מזה של כלי מיתר בכך שהצלילים שהוא מפיק נוצרים על ידי הרעדה של עמודי אוויר בצינורות, ובכך שלרוב צינורות אלה הם סגורים רק למחצה. באקוסטיקה, בקצוות חופשיים יש תמיד נקודת צומת של לחץ הגל, ואילו בקצוות סגורים יש תמיד נקודת טבור שלו. זה נובע מכך שערך הלחץ בקצה החופשי חייב לעמוד תמיד על לחץ האוויר בסביבה המיידית שמחוץ לצינור (הלחץ האטמוספירי), בעוד הקצוות הסגורים מחזירים את גל הלחץ כמעט במלואו ובמופע זהה לזה של הגל הפוגע. בניגוד לכך, להעתק של מולקולות האוויר נקודת טבור בקצה הפתוח (שם הן חופשיות לנוע) ונקודת צומת בקצה הסגור; כלומר בגל קול עומד נוצרת הפרדה בין גל ההעתק המקושר אליו לגל הלחץ המקושר אליו, בשונה מהמצב בגלי קול באוויר הפתוח.
-
1
-
2
באיור 1 מוצג גרף של הלחץ בעמוד אוויר שבצינור פתוח בשני קצותיו, בעוד שבאיור 2 מוצג הלחץ בעמוד אוויר בצינור פתוח למחצה.
כתוצאה מתנאי שפה אלה ניתן להסיק שאורך הגל "המותר" הראשון בצינור פתוח-למחצה באורך L הוא , והתדירות היסודית המתאימה לו היא . בשונה מתרחישים אחרים, כאן אורכי הגל המותרים אינם כוללים את כל המנות השלמות של אורך הגל היסודי, אלא מתקבלים מן הנוסחה , כך שהתדירויות המותרות הן רק ההרמוניות האי-זוגיות של התדירות היסודית.
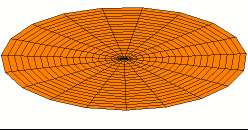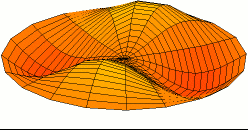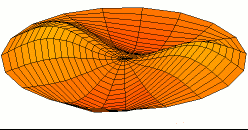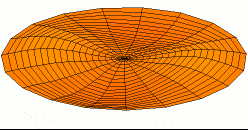
משטח המקובע בקצותיו[עריכת קוד מקור | עריכה]
במשטח המקובע בקצותיו, כמו למשל בתוף, אופני התנודה האפשריים מורכבים יותר מאשר במיתר. אופני התנודה המשטחיים תלויים בצורתו של המשטח ובנקודות או בקווים בהם הוא מקובע.
תיבת תהודה[עריכת קוד מקור | עריכה]
 ערך מורחב – תיבת תהודה
ערך מורחב – תיבת תהודה
גל קול עומד באוויר מתקבל על ידי עירור בקצב מתאים של חלל תהודה כגון תיבת התהודה בגיטרה קלאסית או עמוד האוויר בכלי נשיפה. בגיטרה קלאסית תנודות המיתר מועברות לתיבת התהודה באמצעות הגשר שאליו מחוברים המיתרים.
גלים עומדים בתמסורת[עריכת קוד מקור | עריכה]
זרם חילופין המוזרם דרך קו תמסורת מכיל מידע שצריך להיות מועבר מהמקור ליעד, למשל לאנטנה המיועדת לשידור גלי רדיו. אם קיים תיאום עכבות בין המקור לקו התמסורת ובין קו התמסורת ליעד, לא תהיה החזרה של גלים בעת המעבר מרכיב אחד לאחר. חוסר תיאום עכבות מוביל ליצירת גלים עומדים בקו התמסורת ולהפסדי הספק. יחס גלים עומדים מהווה מדד לתיאום עכבות זה.
באנטנה עצמה נוצר גל עומד של זרם חשמלי ושל מתח חשמלי. אורכה של אנטנה רגילה צריך להיות חצי מאורך הגל של אות הרדיו המשודר. גלים שעבורם אורך האנטנה לא מהווה מכפלה של אורך הגל במספר שלם יונחתו וההספק היוצא מהאנטנה עבורם יהיה קטן יותר.
גל עומד כתוצאה מתנועת התווך[עריכת קוד מקור | עריכה]
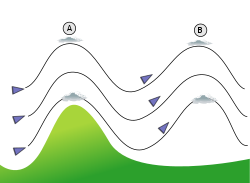
גלי חסי (lee waves; חסי הוא הצד המוגן מפני הרוח) הם דוגמה לגלים עומדים שנוצרים כתוצאה מתנועת גושי אוויר. גלים אלו, שיש להם חשיבות לעוסקים בדאייה, נוצרים כתוצאה מפגיעת הרוח במכשול גדול דוגמת הר. התנודה הראשונה עוקבת אחרי צורת ההר, ותנודות נוספות נוצרות מעל שטחים מישוריים בצד המוגן מפני הרוח. בתנאים של לחות מספקת, נוצרים בקרבת שיאי התנודות עננים הקרויים ענני גל (wave cloud).
גל עומד במים, הקרוי זנק הידראולי, נוצר כשיש שינוי פתאומי במהירות זרימת המים. דוגמאות לגלים עומדים כאלו ניתן למצוא באשדים בנהרות ובמקווי מים בהם קיימים זרמי גאות.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- גל עומד, באתר אנציקלופדיה בריטניקה (באנגלית)
| גלים | ||
|---|---|---|
| מאפיינים | משרעת • תדירות • מופע • אורך גל • וקטור גל • מספר גל • מהירות פאזה • מהירות חבורה • קיטוב | 
|
| תופעות | החזרה • העברה • שבירה • התאבכות • עקיפה • נפיצה • בליעה | |
| מושגים | גל עומד • אפנון • חבילת גלים • תווך • מתנד הרמוני • תהודה • אפקט דופלר | |
| אנליזה | משוואת הגלים • משוואת הלמהולץ • עקרון הויגנס • עקרון פרמה • חוקי פרנל | |
| סוגי גלים | גל מישורי • גל כדורי • גל רוחב • גל אורך • פולס • קרינה אלקטרומגנטית • גל קול • גל (מים) • פונקציית גל | |