השורש הריבועי של 2

השורש הריבועי של 2 הוא אורכו של היתר במשולש ישר-זווית ושווה-שוקיים שאורך ניצביו הוא 1.

השורש הריבועי של 2, ידוע גם כקבוע פיתגורס, לרוב מסומן כ- $\sqrt{2}$ , הוא המספר הממשי החיובי שכאשר יוכפל בעצמו, תהיה התוצאה שווה ל-2. זהו ככל הנראה המספר האי רציונלי הידוע הראשון. השורש הריבועי של 2, מעוגל לחמישים הספרות הראשונות הוא:‏

37695 71875 85696 69807 24209 16887 04880 73095 35623 1.41421

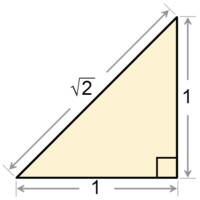
על פי משפט פיתגורס, השורש הריבועי של 2 הוא אורך האלכסון בריבוע שאורך צלעותיו הוא 1.

הקירוב בשברים $\tfrac{99}{70}$ עבור שורש 2 מדויק עד לספרה הרביעית אחרי הנקודה העשרונית.

המספר $\ 1+\sqrt{2}$ נקרא לפעמים "יחס הכסף".

היסטוריה

תבליט נחושת בבלי (המתאורך ל-1800 עד 1600 לפני הספירה) עם הסברים

תבליט נחושת בבלי (המתוארך ל-1800 עד 1600 לפנה"ס) נותן קירוב של $\sqrt{2}$ בדיוק של ארבע ספרות סקסגסימליות שהן כשש ספרות דצימליות:

$.1 + \frac{24}{60} + \frac{51}{60^2} + \frac{10}{60^3} = 1.41421\overline{296}$

אזכור קדום נוסף של $\sqrt{2}$ בקירוב מופיע במסמך הודי עתיק הנקרא "שולבא-סוטרא": "הגדילו את אורך הצלע בשליש ממנה, הוסיפו רבע מן השליש שלה והפחיתו אחד חלקי שלושים וארבע של הרבע שהוספתם" - שזה אומר:

$.1 + \frac{1}{3} + \frac{1}{3 \cdot 4} - \frac{1}{3 \cdot4 \cdot 34} = \frac{577}{408} \approx 1.41421\overline{5686}$

הקירוב ההודי העתיק הוא למעשה המספר השביעי בסדרת פל, והמספרים הבאים בסדרת פל משמשים לקירוב יותר מדויק של השורש הריבועי של 2.

גילוי המספרים האי-רציונליים מיוחס להיפאסוס, מחברי האסכולה הפיתגוראית, שמצא הוכחה שהשורש הריבועי של 2 הוא מספר אי-רציונלי. אולם, דבר הגילוי נשמר בסוד על-מנת שלא לסתור את הטענה של האסכולה הפיתגוראית שהעולם כולו ניתן לתיאור כיחסים בין מספרים טבעיים, והיפאסוס סולק מן האסכולה הפיתגוראית (ולפי גרסאות אחרות הוטבע על ידי פיתגורס ותלמידיו). עם זאת, אין לסיפור זה סימוכין.

חוקרים בני זמננו סבורים כי גילויים של המספרים האי רציונלים, לא זעזע את עולמו של פיתגורס. הם מסבירים שהמקור לאגדה זו הוא שהיוונים בתקופתו של פיתגורס, השתמשו באותה מילה כדי לתאר מספרים אי רציונלים וכדי לתאר תופעה "לא רציונלית" - תופעה שהיא בבחינת "לא תיאמן". קיומם של מספרים אי רציונליים מוזכר לראשונה אצל אפלטון, יותר ממאה שנים לאחר מותו של פיתגורס.

דרכים לחישוב $\sqrt{2}$

ישנן דרכים רבות לחישוב השורש הריבועי של 2 - ניתן להיעזר בשיטות למציאת שורש ריבועי, שהשיטה הבבלית היא אחת מהן. שיטה נוספת היא להיעזר בסדרת פל - ככל שנתקדם בחישוב איברים נוספים של הסדרה נקבל ערך מדויק יותר של השורש הריבועי של 2. למעשה, ניתן לבטא זאת באמצעות שבר משולב:

$\sqrt 2 = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{\ddots\,}}}}}$

מן השבר הזה מתקבלת סדרה של קירובים בשברים: $\ \frac{3}{2}, \frac{7}{5}, \frac{17}{12}, \frac{41}{29}, \frac{99}{70}, \dots$.

בשנת 1996 חושב הערך של השורש הריבועי של 2 עד כדי 137,438,953,444 (כ-137.4 מיליארד) ספרות לאחר הנקודה, על ידי מתמטיקאי יפני, יאסומסה קאנאדה. בשנת 2006 נשבר השיא של חישוב ספרות לאחר הנקודה של השורש הריבועי של 2 והגיע ל-200 מיליארד ספרות לאחר הנקודה; החישוב, במחשב ביתי, נמשך 13 ימים ו-14 שעות.

למעשה, בין הקבועים המתמטיים האי רציונליים (שאינם שבר מחזורי), רק הקירוב של פאי חושב יותר ספרות לאחר הנקודה.

הוכחת אי רציונליות

ישנן הוכחות רבות לאי-רציונליות של שורש 2. ההוכחה המפורסמת ביותר ניתנה על ידי אוקלידס והיא ניתנת כאן:

נניח בשלילה כי קיימים מספרים טבעיים זרים $\ p$ ו-$\ q$ כך ש $\, \left(\frac{p}{q}\right)^2 = 2$. אז $\,p^2 = 2q^2$, ולכן $\ p^2$ זוגי. כיוון שהעלאה של מספר אי-זוגי בריבוע נותנת מספר אי-זוגי, גם $\ p$ זוגי, ולכן $\ p=2m$ כאשר $\ m$ מספר טבעי. נציב ונקבל $\,(2m)^2 = 2q^2$, כלומר $\,2m^2=q^2$. באותו אופן גם $\ q^2$ זוגי, ולכן $\ q$ זוגי - בסתירה להנחה ש-$\ p$ ו-$\ q$ זרים. לכן אין ל-2 שורש רציונלי.

הוכחה לא בונה

שורש 2 משמש תפקיד מרכזי בדוגמה מפורסמת להוכחה לא בונה (הוכחה המראה קיומו של עצם מבלי להראות כיצד ניתן להשיגו). ההוכחה מראה קיום של מספר אי רציונלי בחזקת מספר אי רציונלי הנותן תוצאה רציונלית. נתבונן בשורש 2 בחזקת שורש 2, כלומר: $\sqrt{2}^\sqrt{2}$. אם הוא רציונלי, מצאנו. אחרת, נעלה מספר זה בחזקת שורש 2 ונקבל את התוצאה הרציונלית 2.

בזכות משפט גלפונד-שניידר ידוע כי במקרה הזה $\sqrt{2}^\sqrt{2}$ מספר טרנסצנדנטי ולכן גם אי-רציונלי.

תכונות

השורש הריבועי של 2 הוא מספר אלגברי, ויתר על כן, הוא שלם אלגברי, שכן הוא שורש של הפולינום המתוקן $\,x^2-2\in \mathbb{Z}[x]$.

$\ \sqrt2$ בחזקת עצמו אינסוף פעמים שווה ל-2 (ראו מגדל חזקות).

שימושים

לגליונות ניר בתקן ISO 216 יחס $\sqrt 2$ בין אורכי צלעותיהם. כך יחס הצלעות נשמר בקיפול מדויק של הגיליון לשניים. לדוגמה, מידות דף A4 הן 210 על 297 מילימטרים - יחס מדויק עד הספרה הרביעית אחרי הנקודה העשרונית. סדרות הגליונות בתקן זה מוגדרות כך שכל דף קצר פי $\sqrt 2$ במידות האורך מקודמו בסדרה (A4 קצר פי $\sqrt 2$ מ-A3), וכך תוצאת קיפול או חיתוך גיליון לשנים מתקבלת במידותיו של הגיליון הבא בסדרה.