משתמש:Aizenr/פורטל:מתמטיקה
did u know[עריכת קוד מקור | עריכה]
במתמטיקה כמו במדעי הטבע נהוג לשער השערות על בסיס אינדוקציה (הסקת מסקנות מהפרט אל הכלל). אולם, בשונה ממדעי הטבע, על מנת שהשערה תהפוך למשפט (מתמטיקה) נדרשות גם הוכחות ש"לוכדות את האינסוף" ולא רק מספר סופי של מקרים. על אף שבהרבה מקרים השערות עם ראיות מספריות חזקות מוכחות בסופו של דבר, חלקן מופרכות. תופעה זאת נקראת לעתים חוק המספרים הקטנים.
דוגמה לתופעה זאת הייתה ההשערה לפיה המספרים 31, 331, 3331 וכו' ראשוניים, שהייתה נכונה למספרים הראשונים בסדרה והופרכה רק כשהתגלה ש-333,333,331 פריק.
דוגמה קיצונית אף יותר, גם היא עוסקת במספרים ראשוניים, קשורה למשפט המספרים הראשוניים, שמספק קירוב טוב למספר הראשוניים מתחת למספר . הקירוב נתון על ידי פונציית הלוגוריתם האינטגרלי(אנ') (ששווה בקירוב, פחות מדויק, ל, דהיינו X לחלק לתוצאת הלוגריתם הטבעי עבורו).
לאחר בדיקת כמות עצומה של מספרים, הערכה זו תמיד מפריזה במעט במספר הראשוניים, אך ג'ון אדנזור ליטלווד גילה שבשלב כלשהו הנוסחה תמעיט בכמות המספרים הראשוניים, מבלי להצביע על המספר בו יקרה ההיפוך.
להשערות חשובות כמו המשפט האחרון של פרמה והשערת רימן נמצאו ראיות התקפות למספרים רבים בעזרת מחשבי על. אולם בהעדר הוכחה הן נשארו פתוחות במשך שנים רבות (האחרונה עד היום).
פורטל:מתמטיקה/תמונה נבחרת/64[עריכת קוד מקור | עריכה]
כיסוי האוריינטציות של טבעת מביוס.
כיסוי האוריינטציות הוא כלי לחקר יריעות לא אוריינטביליות. עבור משטח במרחב, ניתן לתאר את כיסוי האוריינטציות באופן הבא: נדמיין שהמשטח עשוי מנייר דו-שכבתי. נפריד את השכבות. היריעה שתתקבל תהיה מרחב הכיסוי של כיסוי האוריינטציות. העתקת הכיסוי תהיה ההדבקה של שתי השכבות בחזרה.
במקרה של טבעת מביוס (זאת אומרת טבעת עם חצי פיתול) היריעה המתקבלת לאחר הפרדת השכבות היא טבעת עם פיתול שלם. יריעה זאת דיפאומורפית לטבעת רגילה, ובפרט אוריינטבילית.
2 did u know[עריכת קוד מקור | עריכה]


המתמטיקאי לאופולד קרונקר היה פיניטיסט(אנ') מושבע. הוא האמין שיש להימנע מבניות מתמטיות שמערבות את האינסוף, ועל אחת כמה וכמה אינסוף לא בן-מנייה. כך גם התנגד נחרצות לתורת הקבוצות שאותה פיתח המתמטיקאי גאורג קנטור, בן זמנו של קרונקר.
במסגרת אידאולוגיה זאת טבע את האמרה:
אלוהים יצר את המספרים הטבעיים, כל היתר הוא מעשה האדם
כיום נהוג להשתמש בציטוט כדי לציין שבניות רבות במתמטיקה מתבססות על מושג המספרים הטבעים (לרבות מושגים אינסופיים בעליל כמו המספרים הממשיים). פרפרזה מודרנית על הציטוט הזה המשויכת לאסקולת בורבקי אומרת:
אלוהים יצר את הקבוצה הריקה, כל היתר הוא מעשה האדם
גרסה זאת מתקשרת לכך שמנקודת המבט של תורת הקבוצות האקסיומטית כל איבר בקבוצה צריך להיות קבוצה בפני עצמיו. מכאן שרק הקבוצה הריקה לא מתבססת על קבוצות אחרות. למשל, מנקודת מבט זאת, נהוג לתאר את קבוצת המספרים הטבעים כך:
תורת הקבוצות האקסיומטית היא הפיתוח המודרני של תורתו של קנטור, בה קרונקר נלחם בלהט.
sors[עריכת קוד מקור | עריכה]
http://www-gap.dcs.st-and.ac.uk/~history/Biographies/Kronecker.html
3 did u know[עריכת קוד מקור | עריכה]


שני הפרדוקסים המרכזיים של תורת הקבוצות הנאיבית, פרדוקס קנטור ופרדוקס ראסל קשורים קשר הדוק.
פרדוקס קנוטור מבוסס על "קבוצת כל הקבוצת". לפי משפט קנטור קבוצת החזקה של "קבוצת כל הקבוצת" חייבת להיות גדולה בעוצמתה מ"קבוצת כל הקבוצת". מה שעומד בסתירה לכך שקבוצת החזקה היא תת-קבוצה של "קבוצת כל הקבוצת".
אם מנתחים את הוכחת משפט קנטור במקרה הזה, מגלים שנקדת המפתח היא חקר "קבוצת כל הקבוצת שאינן איבר של עצמן" אשר מוביל לסתירה. על "קבוצה" זאת מבוסס פרדוקס ראסל.
אפשר לומר כי פרדוקס ראסל הוא מיצוי של הסתירה מתוך פרדוקס קנטור.
jank[עריכת קוד מקור | עריכה]
<center> <math>\begin{multline*}\{ 0=\emptyset,\\ \{ \emptyset\},\\1=\left\{\{ \emptyset,\{ \emptyset\}\right\},\\2=\left\{\emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\}\right\},\\3=\left\{ \emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\}, \{\emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\}\}\right\},\\ \dots \}\end{multline*}</math> </center> <center> <math> \begin{eqnarray} \{0&=&\emptyset, \\ 1&=& \{ \emptyset\}, \\ 2&=&\left\{ \emptyset,\{ \emptyset\}\right\}, \\ 3&=&\left\{\emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\}\right\}, \\ 4&=&\left\{ \emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\},\{\emptyset,\{\emptyset\},\{\{\emptyset,\{\emptyset\}\}\}\right\}, \\ &\dots & \\ n&=& \{0,\dots, n-1\} \\&\dots\}& \end{eqnarray} </math> </center> <center> <math>\begin{eqnarray*} \{0&=&\emptyset, \\ 1&=& \{ \emptyset\}, \\ 2&=&\left\{ \emptyset,\{ \emptyset\}\right\}, \\ 3&=&\left\{\emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\}\right\}, \\ 4&=&\left\{ \emptyset, \{ \emptyset\}, \{\{ \emptyset,\{ \emptyset\}\},\{\emptyset,\{\emptyset\},\{\{\emptyset,\{\emptyset\}\}\}\right\}, \\ &\dots & & \\ n&=& \{0,\dots, n-1\} \\&\dots\}& \end{eqnarray*}</math> </center>
פורטל:מתמטיקה/תמונה נבחרת/9[עריכת קוד מקור | עריכה]

בקבוק קליין, מוטבע במרחב התלת-ממדי. בקבוק קליין הוא משטח קומפקטי לא אוריינטבילי, זאת אומרת שיש לו צד אחד בלבד. למרות שהמשטח הוא דו-ממדי, ודומה למישור בסביבה הקרובה של כל נקודה, הוא אינו ניתן לשיכון במרחב האוקלידי התלת-ממדי, אלא רק במרחב בעל ארבעה ממדים או יותר.
come an help[עריכת קוד מקור | עריכה]
רוצים לעזור? הנה כמה משימות שבהן אתם יכולים לתרום:
- ערכים מבוקשים וערכים טעוני שיפור
- קצרמרים להרחבה
- רשימות אוטומטיות (יש לגלול את המסך כלפי מטה):
כלים[עריכת קוד מקור | עריכה]
- לשיתוף פעולה בנושאי מתמטיקה בקרו בחבורת אוילר - המעדון המתמטי של וויקיפדיה
- לדיונים בנושאי מתמטיקה בקרו בחוג של מרסן
- להסבר על עריכת נוסחאות מתמטיות ראו עזרה:נוסחאות
portal talk head[עריכת קוד מקור | עריכה]
- דיונים כלליים בנושא מתמטיקה בויקיפדיה עדיף לנהל בחוג של מרסן (במקרה הצורך ניתן להשאיר הודעה קצרה כאן ו/או במזנון ו/או בלוח המודעות)
- שאלות מתמטיקה (הרלבנטיות לערכי ויקיפדיה) יש לשאול בהכה את המומחה – שאלות במדעים מדויקים
- דיונים הנוגעים לאחד מדפי המשנה של הפורטל עדיף לנהל בדף השיחה של דף המשנה (במקרה הצורך ניתן להשאיר הודעה קצרה כאן ו/או בחוג של מרסן ו/או בלוח המודעות)
מי יוצא דופן?[עריכת קוד מקור | עריכה]
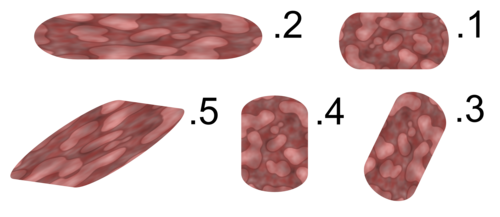
| רמז | |
|---|---|
|
|
| חידת רמז | |||||||
|---|---|---|---|---|---|---|---|
|
| פתרון | |
|---|---|
|
בקשת משוב[עריכת קוד מקור | עריכה]
האם החידה קלה מדי?
Thanks[עריכת קוד מקור | עריכה]
Many thanks to Amirki for he picture.
suggestions to improve the riddle[עריכת קוד מקור | עריכה]
- I suggest to make at list 2 of the pictures deformed by a non linear transformation like the one in 5 in the previous version of the picture
- If the riddle is too easy, one can also the picture with a non text image. (the picture should not be too symmetrical). Then the current picture can serve as another hint.
animation[עריכת קוד מקור | עריכה]
שגיאות פרמטריות בתבנית:תמונות מרובות
פרמטרים ריקים [ 1 ] לא מופיעים בהגדרת התבנית

הגדלה[עריכת קוד מקור | עריכה]
שגיאות פרמטריות בתבנית:תמונות מרובות
פרמטרים ריקים [ 1 ] לא מופיעים בהגדרת התבנית
שגיאות פרמטריות בתבנית:תמונות מרובות
פרמטרים ריקים [ 1 ] לא מופיעים בהגדרת התבנית

שגיאות פרמטריות בתבנית:תמונות מרובות
פרמטרים ריקים [ 1 ] לא מופיעים בהגדרת התבנית
שגיאות פרמטריות בתבנית:תמונות מרובות
פרמטרים ריקים [ 1 ] לא מופיעים בהגדרת התבנית

הנה הרעיון שלי איך לבצעה את ההגדלה. הכנתי 11 פרימים (0-11). ואני צריך להכין עוד 10 (0..-11.., חלקם כבר מוכנים).
את ההגדלה אפשר לבצעה ב11 פרימים: הראשון יהיה "0" השני היה "1" שעליו מונך "..1" עם מקדם שקיפות 90% (מקדם "נראות" 10%). השלישי יהיה "2" שעליו מונך "..1" עם מקדם שקיפות 80% (מקדם "נראות" 90%). כך הלה עד האחרון שהיה 11...
הערות:
- יש בעיה עם "7". אני לא מצליח להאלות אתו כמו שצריך (אולי צריך לט לו זמן להתעדכן).
- ניסיתי למקם את התמונות כך שהם יתאימו אחת לשניה (לםחל 0 ו0.. צריכות להיות באותו מקום). אני לא בטוח שהצלחתי, אני לי את הכלים ליבדוק את זה
- ההגדלה כאן היא פי 2. בפועל צריך הגדלה מעת גדולה יותר. מה מקדם האמיתי?
מה דעתך? האם זה יעבוד? האם לצור את התמונות החסרות?
בקשה נוספת:
- בסוף כדאי ליצור גם אנימציה בגודל מלא (כמו הגודל המקורי) כך יהיה אפשר לקשר אלה מה אנימציה המוקטנת בפורטל כדי שהיה אפשר לראות את הפרטים טוב יותר.
תודה רבה. רמי (Aizenr) - שיחה 22:07, 5 ביוני 2013 (IDT)