פוטון
 | |
| פוטונים הנפלטים בקרן קוהרנטית מלייזר | |
| מידע כללי | |
|---|---|
| הרכב | חלקיק יסודי |
| סטטיסטיקה | בוזון |
| קבוצת שיוך | בוזון כיול |
| אנטי-חלקיק | עצמו |
| סמל | γ |
| תכונות | |
| מסת מנוחה |
0 kg 0 MeV/c2 |
| מטען חשמלי | 0 e |
| ספין | 1 ħ |
| מספר לפטוני | 0 |
| מספר באריוני | 0 |
| מטען צבע | 0 |
| אינטראקציות | אלקטרומגנטיות, הכוח החלש, כבידה |
| אורך חיים | יציב |
| היסטוריה | |
| נצפה? | כן |
| תאריך גילוי | 1905[א] |
| הכרה | פרס נובל לפיזיקה לשנת 1921 |
פֿוֹטוֹן (Photon) הוא חלקיק יסודי, המהווה את הקוונטום של השדה האלקטרומגנטי ונשא הכוח של הכוח האלקטרומגנטי. הפוטון הוא בוזון כיול, נטול מסה ומטען חשמלי, בעל ספין של 1. כל פוטון נושא אנרגיה ומהווה מנה (קוונטום) של קרינה אלקטרומגנטית, לרבות אור וגלי רדיו. אנרגיית הפוטון נקבעת אך ורק לפי התדר או לפי אורך הגל של הפוטון (לחלופין, התדר ואורך הגל נקבעים לפי אנרגיית הפוטון). ההבדל בין אנרגיות פוטון שונות אחראי למגוון רחב של תופעות, לרבות מגוון צבעי האור הנראה, תדרים שונים של שידורי רדיו, ההבחנה בין קרינה מייננת לקרינה בלתי מייננת ועוד.
לפוטון, כמו לכל חלקיקי היסוד האחרים, ישנן תכונות הן של גל והן של חלקיק, תופעה המכונה "דואליות גל-חלקיק".[1] התופעות דמויות-הגל שמציגים פוטונים הן, לדוגמה, שבירה על ידי עדשה והתאבכות. התכונות החלקיקיות של הפוטון הן, בין השאר, פיזור והעברת אנרגיה במנות בדידות. פוטון שעובר אינטראקציה מלאה עם אטום או עם מולקולה נבלע ומוסר, או נפלט ומקבל, את כל האנרגיה שלו תוך כך. בעקבות האינטראקציה עוברים האטום או המולקולה עירור או יינון. עבור אור בתחום הנראה, האנרגיה הנישאת על ידי פוטון יחיד של אור ירוק לדוגמה היא כ-4×10-19 ג'ול בקירוב, כמות אנרגיה המספיקה לעורר מולקולה יחידה של תא קולט אור בעין, וליצור בכך אות עצבי שהוא הבסיס הפיזיולוגי לראייה.
פוטונים מקיימים מגוון רחב של אינטראקציות עם חומר, כגון אפקט קומפטון, בו משנה הפוטון את האנרגיה אותה הוא נושא ולכן גם את אורך הגל שלו,[2] ויצירת זוג, תהליך בו אלקטרון ופוזיטרון נוצרים מפוטון בודד העובר ליד אטום.[3] פוטונים יכולים להיפלט מגרעין אטום לא יציב בצורת קרינת גמא, וכמו כן הם יכולים להיפלט על ידי חלקיקים טעונים הנמצאים בתאוצה.[4]
באלקטרודינמיקה קוונטית, הפוטון משמש כמתווך בתהליכים אלקטרומגנטיים, כלומר, האינטראקציה מתרחשת באמצעות החלפת פוטונים בין חלקיקים טעונים. למעשה, כל השדות החשמליים והמגנטיים ניתנים לתיאור באמצעות פוטונים. לפי המודל הסטנדרטי של פיזיקת החלקיקים, קיום הפוטון הוא תוצאה של הדרישה כי לחוקים הפיזיקליים תהיה סימטריה מסוימת בכל נקודה במרחב-זמן. תכונות הפוטונים, כגון מטען חשמלי, מסה וספין, נקבעות על ידי מאפייני סימטריה זו (סימטריית כיול).
הרעיון כי האור נישא במנות בדידות, כלומר באמצעות פוטונים, פותח על ידי אלברט איינשטיין החל מ-1905.[5] איינשטיין פירש את הנוסחה שהציע מקס פלאנק על מנת להסביר את הספקטרום של קרינת גוף שחור:
- E = hν
כאשר h הוא קבוע פלאנק. איינשטיין זיהה את E עם אנרגיית קוונט אחד של קרינה אלקטרומגנטית, שלימים נקרא פוטון, ואת ν עם תדר הקרינה. באמצעות מודל הפוטונים, הצליח איינשטיין להסביר את האפקט הפוטואלקטרי. הנוסחה E = hν מכונה נוסחת פלאנק-איינשטיין (Planck-Einstein formula). יחד עם הפיזיקאי ההודי סאטינדרה נאת בוז, סיפק איינשטיין תיאור סטטיסטי של אור, המסביר את קרינת פלאנק. בנוסף, מתוך שיקולים סטטיסטיים, הסיק איינשטיין את קיומו של מנגנון הפליטה המאולצת, וכן מצא קשרים בין מקדמי הבליעה והפליטה של אור על ידי חומר.
גילוי מודל הפוטון הביא לפריצות דרך בפיזיקה הניסויית והתאורטית, כגון פיתוח הלייזרים, יצירת עיבוי בוז-איינשטיין ובאופן כללי הביא להתפתחות מכניקת הקוונטים. תחומים רבים אחרים התקדמו בזכות הבנת מושג הפוטון, למשל פוטוכימיה, מיקרוסקופיה בהפרדה גבוהה ומדידת מרחקים ברמה המולקולרית. בתחילת המאה ה-21 נמצא שימוש לפוטונים בודדים במחקרים העוסקים במחשוב קוונטי וביישומי תקשורת אופטית מתקדמים, כגון הצפנה קוונטית.
אטימולוגיה[עריכת קוד מקור | עריכה]
במאמרו המקורי מ-1905 נתן אלברט איינשטיין לפוטון את השם "קוונט האור" (בגרמנית: "das Lichtquant").[6] מקור השם המודרני "פוטון" הוא במילה היוונית "פוס" (אור). השם נטבע ב-1926 על ידי הכימאי גילברט ניוטון לואיס, שפרסם תאוריה ספקולטיבית שלפיה פוטונים בלתי ניתנים ליצירה או להשמדה.[7] התאוריה של לואיס לא התקבלה, מאחר שהיא נסתרה על ידי ניסויים רבים, אך השם החדש "פוטון" אומץ מיד על ידי רוב הפיזיקאים. דעה אחרת מוצגת בספרו של אייזק אסימוב "הנייטרינו, חלקיק הרפאים של האטום" (1966). אסימוב זוקף לזכותו של ארתור קומפטון את הגדרת קוונט האור כפוטון ב-1927.
בפיזיקה, הפוטון מסומן בדרך-כלל באות היוונית גמא, γ. מקור הסמל, ככל הנראה, בקרינת גמא. קרניים אלה התגלו ב-1900 על ידי פול אולריך וילארד. ב-1914 הראו ארנסט רתרפורד ואדוארד אנדרד שהן למעשה קרינה אלקטרומגנטית. בכימיה ובהנדסה אופטית, פוטונים וקרינה אלקטרומגנטית מסומנים פעמים רבות hν.[ב]
היסטוריה[עריכת קוד מקור | עריכה]


רוב תאוריות האור עד המאה ה-18 תיארו את האור כעשוי מחלקיקים. אחת מהתאוריות החלקיקיות המוקדמות ביותר נוסחה על ידי אבן אל-היית'ם בספרו "ספר האופטיקה" מ-1021. קרני האור תוארו שם כזרמי חלקיקים זערוריים "חסרי תכונות מוחשיות למעט אנרגיה". מאחר שהמודלים החלקיקיים של האור אינם מסבירים בקלות תופעות כגון שבירה, עקיפה ושבירה כפולה, הוצעו מאוחר יותר תאוריות גליות על ידי רנה דקארט (1637), רוברט הוק (1665) וכריסטיאן הויגנס (1678); למרות זאת, המודלים החלקיקיים נותרו דומיננטיים, בעיקר עקב השפעתו של אייזק ניוטון. בתחילת המאה ה-19 הראו תומאס יאנג ואוגוסטן פרנל כי האור מקיים תופעות התאבכות ועקיפה, ועד 1850 המודלים הגליים כבר היו מקובלים על רוב המדענים. ב-1865 שיער ג'יימס קלרק מקסוול, באמצעות המשוואות שפיתח, כי האור הוא גל אלקטרומגנטי, והשערה זו אושרה כשהיינריך הרץ גילה את גלי הרדיו. התגלית נדמתה כסותמת את הגולל על המודלים החלקיקיים של האור.[8][9]
למרות האמור לעיל, תאוריית הגלים של מקסוול לא הסבירה את כל תכונות האור. תאוריית מקסוול גורסת כי אנרגיית הגל תלויה אך ורק בעוצמתו, ולא בתדירותו; אף על פי כן, מספר ניסויים בלתי תלויים הראו כי האנרגיה שהאור מעניק לאטומים כן תלויה בתדירות שלו, ולא בעוצמה. לדוגמה, חלק מהתגובות הכימיות נגרמות רק על ידי אור שתדירותו גבוהה מערך סף מסוים; אור בתדירות נמוכה מהסף, ללא תלות בעוצמתו, לא יגרום לתגובה. באותו אופן ניתן לקרוע אלקטרונים ממשטח מתכתי על ידי הארתו בתדירות גבוהה מספיק. זהו האפקט הפוטואלקטרי. אנרגיית האלקטרון הנפלט נקבעת לפי תדירותו של האור, ולא לפי עוצמתו.
במקביל, המחקרים בקרינת גוף שחור שבוצעו במשך ארבעה עשורים (1860-1900) על ידי חוקרים רבים הגיעו לשיאם בהשערה של מקס פלאנק כי האנרגיה של כל מערכת הקולטת או פולטת קרינה אלקטרומגנטית עם תדר ν היא כפולה שלמה של קוונט האנרגיה E = hν. אלברט איינשטיין הראה כי אם מניחים צורה כלשהי של קוונטיזציית אנרגיה, ניתן להסביר את שיווי המשקל התרמודינמי הנצפה בין החומר והקרינה האלקטרומגנטית. עבור הסבר זה של האפקט הפוטואלקטרי, קיבל איינשטיין את פרס נובל לפיזיקה ב-1921.
מאחר שתאוריית האור של מקסוול מאפשרת לקרינה אלקטרומגנטית לקבל כל ערך שרירותי של אנרגיה, רוב הפיזיקאים הניחו שקוונטיזציית האנרגיה נובעת ממגבלה בלתי-ידועה כלשהי של החומר שספג ופלט את הקרינה, ולא מגבלה על הקרינה עצמה. ב-1905, היה איינשטיין הראשון להעלות את ההשערה שקוונטיזציית האנרגיה היא תכונה של הקרינה האלקטרומגנטית עצמה. אף על פי שאיינשטיין קיבל את תקפותה של תאוריית מקסוול, הוא הצביע על כך שניתן להסביר תוצאות של ניסויים רבים שלא עלו בקנה אחד עם התאוריה, אם אנרגיית גלי האור הייתה מרוכזת בקוונטים נקודתיים אשר נעו בנפרד אחד מהשני, אפילו אם הגל עצמו נפרש באופן רציף בחלל. ב-1909 וב-1916 הראה איינשטיין כי לפי חוק פלאנק לקרינת גוף שחור, קוונטי האנרגיה חייבים לשאת גם תנע המוגדר על ידי p = h / λ, ולכן ניתן להתייחס אליהם כאל חלקיקים יסודיים במלוא מובן המילה. תנע הפוטון נצפה בניסוי על ידי ארתור קומפטון, ועל כך הוא קיבל את פרס נובל לפיזיקה ב-1927. נתונים אלו העלו את השאלה החשובה שהעסיקה פיזיקאים רבים: כיצד לאחד את התאוריה הגלית של מקסוול עם טבעו החלקיקי של האור כפי שנצפה בניסוי. התשובה לשאלה זו העסיקה את איינשטיין בשארית חייו, ונפתרה לבסוף באמצעות אלקטרודינמיקה קוונטית וממשיכת דרכה, תאוריית המודל הסטנדרטי.
תכונות פיזיקליות[עריכת קוד מקור | עריכה]

הפוטון חסר מסה[ג] וחסר מטען חשמלי, ואינו מתפרק באופן ספונטני בריק. מהירות האור בריק, c, היא קבוע שערכו 299,792,458 מטרים לשנייה. לכן, פוטון לא יכול להימצא במצב מנוחה. יש לו שני מצבי קיטוב אפשריים, וניתן לתארו על ידי שלושה פרמטרים רציפים בדיוק: רכיבי וקטור הגל שלו. הם קובעים את אורך הגל λ וכיוון ההתפשטות של הפוטון. פוטון נע במסלול גאודזי ממוצע, כלומר בדרך הקצרה ביותר במרחב-זמן. פוטון נושא אנרגיה ותנע הקשורים זה לזה בהתאמה לאורך הגל שלו, כפי שמודגם בניסוח האפקט הפוטו-אלקטרי ובמשוואת דה ברויי.
פוטון הוא חלקיק אלמנטרי מסוג בוזון, כלומר חלקיק בעל ספין שלם המציית לסטטיסטיקת בוז-איינשטיין, ולכן ניתן לדחוס מספר לא מוגבל של פוטונים לתוך אותו מצב קוונטי.[ד] לפוטון ספין שלם של 1 אך מכיוון שהוא חסר מסה, יש לו בורגיות מוגדרת ולכן הספין יכול לקבל רק את הערכים .
על פי תורת השדות, הפוטון הוא בוזון הכיול של הכוח האלקטרומגנטי, כלומר, הכוחות החשמליים והמגנטיים הם תוצר של החלפת פוטונים. כל שאר המספרים הקוונטים של הפוטון, כגון מספר לפטוני, מספר באריוני ומוזרות, הם אפס בדיוק. מכיוון שמסת הפוטון היא 0, הכוח החשמלי הוא כוח ארוך טווח (למעשה, בעל טווח אינסופי) ועוצמתו פרופורציונלית לאחד חלקי המרחק בריבוע. זאת, בניגוד, לדוגמה, לגלואון, הנושא את הכוח החזק. אף שגם הגלואון הוא בעל מסה של 0, הרי שלגלואון עצמו יש מטען צבע. כתוצאה מכך, הגלואונים נמשכים זה לזה בעוצמה רבה; תגובה זו מקצרת את טווח הפעולה של הגלואונים ומביאה לכך שהכוח החזק הוא כוח קצר טווח, כאשר מרבית האינטראקציה החזקה מתקיימת בתוך הקוטר של האדרון בודד.
פוטונים נפלטים בתהליכים טבעיים רבים. לדוגמה, כאשר חלקיק טעון מואץ בעת מעבר מולקולרי, אטומי או גרעיני לרמת אנרגיה נמוכה יותר, או כאשר חלקיק ואנטי-חלקיק שלו מתאיינים. פוטונים נבלעים בתהליכים ההפוכים (מבחינת סדר התרחשותם) לתהליכים המוזכרים לעיל: לדוגמה, ביצירת זוג של חלקיק ואנטי-חלקיק או במעבר מולקולרי, אטומי או גרעיני לרמת אנרגיה גבוהה יותר.
האנרגיה והתנע של פוטון[עריכת קוד מקור | עריכה]
בחלל ריק, הפוטון נע במהירות האור, c. בין האנרגיה שלו E לבין התנע שלו קיים יחס הנפיצה הבא: . לשם השוואה, המשוואה המתאימה לחלקיקים עם מסת מנוחה m, כפי שהיא מנוסחת בתורת היחסות הפרטית, היא: .
אנרגיית הפוטון תלויה רק בתדירות ν או באורך הגל λ שלו, שכן ו-h הוא קבוע פלאנק):
כאשר הוא קבוע פלאנק המצומצם ו- , תדירות זוויתית.
התנע של הפוטון תלוי אך ורק באורך הגל שלו:
כאשר הוא וקטור הגל (שגדולו הוא ). כיוון ה- מצביע לכיוון התקדמות של הפוטון.
לעומת זאת, הספין של הפוטון אינו תלוי בתדירותו. גודל הספין הוא ורכיבו הנמדד בכיוון התנועה חייב להיות , כאשר פלוס מתאים לספין "מעלה" ומינוס לספין "מטה". שתי אפשרויות אלו מתאימות לשני מצבי הקיטוב המעגלי של הפוטון (קיטוב ימני וקיטוב שמאלי).
כאשר חלקיק והאנטי-חלקיק שלו מתאיינים, חייבים להיווצר לפחות שני פוטונים. במערכת הייחוס ביחס למרכז המסה של החלקיקים המתנגשים, אין להם תנע כולל, בעוד שלפוטון יחיד תמיד יש תנע (מאחר שהוא תלוי, כאמור, בתדירות או באורך הגל בלבד, והם אינם אפס). לכן, חוק שימור התנע דורש כי ייווצרו לפחות שני פוטונים, והתנע הכולל שלהם במערכת יהיה זהה לשל החלקיקים, כלומר אפס. ניתן לקבוע את התדירות והאנרגיה של שני החלקיקים באמצעות חוק השימור של ארבע תנע[ה] פרשנות נוספת גורסת כי הפוטון יכול להיחשב כאנטי-חלקיק של עצמו. התהליך ההפוך לזה שתואר לעיל, יצירת זוג, הוא אחד המנגנונים שגורמים לפוטונים באנרגיה גבוהה, כמו קרני גמא, לאבד אנרגיה בעת שהם עוברים דרך חומר.
את הנוסחאות לאנרגיה ולתנע של קרינה אלקטרומגנטית ניתן לבטא מחדש במונחים של פוטונים. לדוגמה, לחץ הקרינה של קרינה אלקטרומגנטית על עצם נובע מהעברת התנע של הפוטונים למשטח הפגיעה. כאשר מחשבים את התנע ליחידת זמן ויחידת שטח מקבלים יחידות של לחץ.
העובדה שלפוטון יש תנע זכתה למגוון רחב של יישומים. במלקחיים אופטיים ניתן להחזיק כדורי זכוכית קטנים בעזרת קרן לייזר הממוקדת לנקודה במרחב. עקרון הפעולה של מלקחיים אלו מבוסס על כך שהפוטונים הנשברים בכניסה וביציאה מכדור הזכוכית, מעבירים לכדור תנע הדוחף אותו לכיוון המוקד של קרן הלייזר. כמו כן, טכניקות של קירור אטומים על ידי לייזר מבוססות גם הן על כך שאטומים הבולעים פוטונים מקבלים תנע, היכול לשמש לקירורם.
דואליות גל-חלקיק ועקרון אי-הוודאות[עריכת קוד מקור | עריכה]
פוטונים מקיימים דואליות גל-חלקיק, כלומר מראים הן תכונות של גלים והן תכונות של חלקיקים, בהתאם לסוג הניסוי[10]. הפוטון מציג תופעות גליות, כגון עקיפה והתאבכות, בקנה המידה של אורך הגל שלו. פוטון יחיד העובר בניסוי שני הסדקים פוגע במסך בהתפלגות הנקבעת לפי תבנית ההתאבכות המתאימה למשוואות מקסוול. אף על פי כן, ניסויים ממחישים כי שהפוטון אינו פעימה קצרה של גל אלקטרומגנטי, בדומה לפעימות של גלי ים או גלי קול; הוא אינו מתפרש בחלל בעת תנועתו, ואינו מתחלק לשניים כאשר הוא נתקל במפצל קרניים. במקום זאת, נראה הפוטון כחלקיק נקודתי, מאחר שהוא נפלט או נבלע בשלמותו על ידי מערכות קטנות באופן שרירותי, קטנות בהרבה מאורך הגל שלו. דוגמאות למערכות כאלה הן גרעין האטום, אשר קוטרו הוא מסדר גדול של פמטומטר אחד, או אפילו האלקטרון, שמקיים דואליות גל-חלקיק בעצמו. למרות זאת, הפוטון אינו חלקיק נקודתי שמסלולו נקבע באופן הסתברותי על ידי השדה האלקטרומגנטי, כפי שסברו בעבר; הנחה זו הופרכה אף היא על ידי הניסויים המתוארים בסוף הפסקה הקודמת. לפי גישות מודרניות, המודל הסטנדרטי רואה בפוטונים בוזני כיול של הכוח האלקטרומגנטי[11].

יסוד עיקרי במכניקת הקוונטים הוא עקרון אי-הוודאות של הייזנברג, אשר לפיו לא ניתן למדוד בו-זמנית את המיקום ואת התנע של חלקיק בכיוון מסוים. למעשה, עקרון אי-הוודאות עבור חלקיקים חומריים טעונים מחייב את הקוונטיזציה של האור לפוטונים, וכן את התלות של האנרגיה והתנע של הפוטון בתדירותו. המחשה לכך ניתן למצוא בניסוי המחשבתי של הייזנברג, בו מוצאים את מיקומו של אלקטרון באמצעות מיקרוסקופ אידיאלי (ראו מסגרת). מיקום האלקטרון יכול להיקבע רק עד לרמת ההפרדה הזוויתית של המיקרוסקופ, אשר ניתנת באמצעות הנוסחה הבאה מתחום האופטיקה הקלאסית:
כאשר זה אורך גל של האור ו היא זווית הפתח במיקרוסקופ. מנוסחה זו נובע כי אי-הוודאות במיקום יכולה להיות קטנה ככל הנדרש באמצעות הקטנת אורך הגל . בתנע של האלקטרון איננו יכולים להיות בטוחים, מאחר שהוא קיבל "פעימה" מהאור שפגע בו והתפזר אל תוך המיקרוסקופ. אם האור לא היה בדיד, אי-הוודאות הייתה יכולה להיעשות קטנה ככל הנדרש על ידי הקטנת עוצמת האור. במקרה זה, מאחר שניתן לשלוט באורך הגל ובעוצמת האור באופן בלתי-תלוי, ניתן למדוד את המיקום והתנע של האלקטרון במידת דיוק גדולה ככל הנדרש, וזוהי הפרה של עקרון אי הוודאות. לעומת זאת, הנוסחה של איינשטיין לתנע של הפוטון משמרת את עקרון אי הוודאות: מאחר שהפוטון עשוי להתפזר בכל מקום, אי-הוודאות בתנע שהועברה שווה ל-
ומכאן נובע היחס , הוא עקרון אי-הוודאות של הייזנברג. מכאן, היקום כולו הוא בדיד; הן החומר והן השדות חייבים לציית למערכת עקבית של חוקים קוונטים, ולא ייתכן שרק אחד מהם יהיה בדיד והשני לא.
עקרון אי-ודאות נוסף קובע כי לא ניתן למדוד בו זמנית את המספר של פוטונים בגל אלקטרומגנטי ואת המופע של אותו גל:
למידע נוסף, ראו מצבים קוהרנטיים.
בניסוי שני הסדקים, נוצרת תבנית התאבכות הן במקרה של פוטונים והן במקרה של חלקיקים חומריים כגון אלקטרונים. כאשר מדובר בפוטונים, זוהי תבנית ההתאבכות הנובעת ממשוואת הגל האלקטרומגנטי של מקסוול, ואילו כאשר מדובר בחלקיקים חומריים, זוהי תבנית ההתאבכות הנובעת ממשוואת שרדינגר. אומנם דמיון זה עשוי לגרום לנו לחשוב כי משוואות מקסוול הן פשוט משוואת שרדינגר במקרה הפרטי של פוטונים, אך רוב הפיזיקאים אינם סבורים כך. ראשית, קיימים הבדלים מתמטיים; ההבדל הברור ביותר הוא כי את המשוואה (היחידה) של שרדינגר פותרים בשדה מרוכב, ואילו את (ארבעת) המשוואות של מקסוול פותרים בשדה ממשי. באופן כללי יותר, המושג של פונקציית גל הסתברותית אינו ישים לגבי פוטונים. מאחר שלפוטונים אין מסה, לא ניתן להגבילם למקום מסוים מבלי להשמיד אותם; בצורה טכנית יותר, לפוטונים לא יכול להיות מצב עצמי הקובע את המיקום, ומכאן עקרון אי הוודאות הרגיל של הייזנברג אינו תקף לגבי פוטונים. מספר פונקציות גל חלופיות הוצעו בעבר עבור הפוטון, אך אף אחת מהן לא נמצאת בשימוש נפוץ. במקום זאת, הפיזיקאים מקבלים את תאוריית הקוונטיזציה השנייה של הפוטונים המתוארת להלן, אלקטרודינמיקה קוונטית, ובה הפוטונים הם עירורים בדידים של מצבים אלקטרומגנטיים.
מודל בוז-איינשטיין לגז פוטונים[עריכת קוד מקור | עריכה]
ב-1924, הוכיח הפיזיקאי סאטינדרה נאת בוז את חוק פלאנק לקרינת גוף שחור ללא כל שימוש באלקטרומגנטיות, אלא באמצעות התאמה של תהליך מסוים במרחב מופע. איינשטיין הראה כי התאמה זו שקולה להנחה כי הפוטונים הם זהים לחלוטין, הנחה שמרמזת על קיומה של "אינטראקציה לא מקומית מסתורית", שכיום מבינים אותה כדרישה למצב קוונטי סימטרי. גילויים אלו הובילו להגדרת המושג מצבים קוהרנטיים, ולפיתוחו של הלייזר. בנוסף, הרחיב איינשטיין את ההוכחה של בוז לחלקיקים חומריים (בוזונים), וניבא כי הם יתעבו למצב הקוונטי הנמוך ביותר שלהם בטמפרטורות נמוכות מספיק. תופעה זו, עיבוי בוז-איינשטיין, נצפתה בניסוי ב-1995. השימוש במילה "עיבוי" בהקשר זה הוא אנלוגיה לתהליך העיבוי, שבו חומר רגיל עובר ממצב צבירה גז לנוזל.
על מנת לאפשר סופרפוזיציה של שדות אלקטרומגנטים, המצב בו משוואות מקסוול הן ליניאריות, על הפוטונים לפעול לפי התפלגות בוז-איינשטיין. כל החלקיקים נחלקים לבוזונים - בעלי ספין שלם, ולפרמיונים, בעלי ספין לא שלם שהוא כפולה של 1⁄2. משפט ספין-סטטיסטיקה מראה כי כל הבוזונים מצייתים להתפלגות בוז-איינשטיין, ואילו כל הפרמיונים מצייתים להתפלגות פרמי-דיראק, או, באופן שקול, לעקרון האיסור של פאולי. עקרון האיסור קובע כי שני פרמיונים זהים אינם יכולים להימצא באותו מצב קוונטי בו-זמנית. מכאן, אם הפוטון היה פרמיון, רק פוטון אחד היה יכול לנוע בכיוון מסוים בזמן נתון, וזאת בסתירה לתצפית הניסויית שלפיה לייזרים מסוגלים לייצר אור קוהרנטי, שבו פוטונים רבים נעים באותו כיוון בדיוק. מכאן, הפוטון חייב להיות בוזון ולציית להתפלגות בוז-איינשטיין. (ראו גם: גז בוז).
אינטראקציה בין פוטונים לחומר[עריכת קוד מקור | עריכה]
על פי התמונה הקלאסית, כלומר על פי משוואות מקסוול, האור מורכב משדות חשמליים ומגנטיים המתנדנדים בזמן. משום כך, כאשר אור עובר בקרבת חומר טעון הוא גורם לו להתנדנד. בתהליך זה, עוברת אנרגיה מהאור לחומר ונוצרת בליעה של אור. באותו אופן יכול להתרחש גם התהליך ההפוך: מטענים טעונים המשנים את מהירותם יוצרים שדות חשמליים ומגנטיים משתנים, ולפיכך פולטים אור. תהליכים אלו תוארו לראשונה באופן תאורטי על ידי ג'יימס מקסוול ואוששו באופן ניסיוני לראשונה על ידי היינריך רודולף הרץ.
התמונה הקוונטית של אותם תהליכים היא, שכאשר פוטון עובר בקרבת מערכת קוונטית, כגון אטום, הוא יכול להיבלע, בעוד המערכת עוברת למצב קוונטי גבוה יותר, בהתאם לאנרגיה של הפוטון. התהליך ההפוך הוא שמערכת יורדת ממצב מעורר למצב נמוך יותר, תוך כדי פליטת פוטון. תהליכים אלו הם חד-פוטוניים, והם יוצרים את מגוון התופעות שנחקרות במסגרת האופטיקה הליניארית. בנוסף, ישנו מגוון רחב של תהליכים שבהם מעורב יותר מפוטון אחד (תהליכים רב-פוטוניים), ואלה יוצרים את התופעות של האופטיקה הלא ליניארית.
בליעה ופליטה של פוטון בודד - יצירת הספקטרום האלקטרומגנטי[עריכת קוד מקור | עריכה]
כאמור, כאשר פוטון עובר בקרבת מערכת קוונטית הוא יכול להיבלע בה, בתנאי שאנרגיית הפוטון מתאימה לאנרגיה של מעבר רמות בתוך החומר. חלקים שונים של הספקטרום האלקטרומגנטי מתאימים לסוגים שונים של עירורים של החומר. להלן מספר דוגמאות:
- גלי רדיו (אורך גל 1 קילומטר - 1 סנטימטר) - גלים אלו מתאימים לפלזמונים המתארים תנודה של אלקטרונים בתוך מתכות.
- קרינה תת-אדומה (אורך גל 1 מילימטר - 750 ננומטר) - קרינה זו מתאימה לעירור של רוטציות ויברציות במולקולות.
- אור נראה וקרינה אולטרה סגולה (אורך גל 750 ננומטר - 10 ננומטר) - קרינה זו מתאימה למעברים אלקטרוניים באטומים ובמולקולות.
- קרני רנטגן (אורך גל 10 ננומטר - 5 פיקומטר) - מתאימה ליינון של מולקולות.
- קרני גמא (אורך גל קטן מ-5 פיקומטר) - פיזיקה גרעינית (עירורים שונים המתרחשים בתוך גרעין האטום), תהליכי יצירת זוג (בהם נבלע פוטון ונוצר חלקיק ואנטי חלקיק שלו, כמו יצירת אלקטרון ופוזיטרון).
האופטיקה הליניארית[עריכת קוד מקור | עריכה]
תהליכים אלו של בליעה, פליטה ופליטה של אור אחראים לתופעות השייכות לתחום האופטיקה הליניארית, כגון בליעה של אור (בחומרים שאינם שקופים), פיזור אור והחזרת אור כתוצאה מפליטה, וכן האטה של מהירות האור הנע בתוך חומר היוצרת את אפקט השבירה של האור. בתופעות אלו נעשה שימוש באופטיקה על מנת ליצור מראות ועדשות, המשמשות למגוון רחב של יישומים הכוללים טלסקופים, מיקרוסקופים, משקפיים, וכדומה.
מקורות אור, כמו נורות ועדשות, מבוססים על תופעת הפליטה הספונטנית. בנורות חשמל רגילות, כמו גם בכוכבים, החום הגדול של חוט הלהט גורם לכך שהאטומים בחוט מעוררים, ופולטים את האנרגיה שלהם בצורת פוטונים, הנפלטים בספקטרום הנקרא קרינת גוף שחור. בנורות ניאון, או בנורות שמבוססות על גזים אחרים, נעשה שימוש בהתפרקויות חשמליות על מנת לעורר את האטומים לרמות גבוהות, וכתוצאה מכך נפלט אור בתדרים המאפיינים את האטומים בגז.
כפי שצוין, לפוטונים יש לא רק אנרגיה אלא גם תנע, ולכן אטום הבולע או הפולט אור מקבל גם "דחיפה" בכיוון או נגד הכיוון שבו נפלט האור. על בסיס תופעה זו הומצאו שיטות לקירור אטומים באמצעות אור. שיטות אלו איפשרו קירור אטומים לטמפרטורה הקרובה לאפס המוחלט והביאו לשורה של תגליות, כגון שעונים אטומיים, יצירתם של גלי חומר ושל עיבוי בוז-איינשטיין ותופעות אחרות.
תופעות מסדרים גבוהים יותר - אופטיקה לא ליניארית[עריכת קוד מקור | עריכה]
בנוסף לבליעה ולפליטה של פוטון בודד, יכולים להתרחש תהליכים בהם מעורב מספר רב יותר של פוטונים.
אור יכול לבלוע שני פוטונים במקביל אם סכום האנרגיות שלהם מתאים למעבר רמה בתוך האטום. תהליך זה אסור משיקולי סימטריה בחומר איזוטרופי, אך קורה במצבים שבהם הסימטריה נשברת. השימוש העיקרי בתהליך זה הוא בגבישי הכפלה, המשמשים להכפלת תדר האור היוצא מלייזרים. התופעה ההפוכה גם היא אפשרית - אטום מעורר יכול לדעוך לרמת היסוד על ידי פליטה של שני פוטונים שסכום האנרגיות שלהם שווה למעבר הרמה שלו. תופעה זו משמשת לבנייה של לייזרים מסוג OPO, שהם לייזרים שניתן לשלוט בנקל על אורך הגל שלהם. לתופעה זו יש גם שימושים רבים באופטיקה קוונטית, כפי שיוסבר בהמשך.
תופעת רמן היא תופעה שבה שני פוטונים בעלי אנרגיות שונות פוגעים במולקולה וגורמים לה לעלות לרמה גבוהה ומיד אחר-כך לרדת לרמה נמוכה השונה מרמת היסוד. באופן זה המולקולה בולעת אנרגיה כוללת השווה להפרש האנרגיות של שני האטומים, וכך, לדוגמה, ניתן לחקור רמות ויברציה של מולקולות בעזרת שני פוטונים באורכי גל של האור הנראה, במקום בעזרת פוטונים תת-אדומים.
התהליך הלא ליניארי החשוב ביותר הוא תהליך שבו שני פוטונים נבלעים ופוטון אחד נפלט בו זמנית. תהליך זה נקרא תופעת קר (Kerr effect). תהליך זה איננו אסור משיקולי סימטריה, ולכן הוא מתרחש, אם כי בסבירות נמוכה (ולכן ניתן להבחין בו רק כאשר עוצמת האור גבוהה מאוד) בכל מעבר שהוא של אור בחומר. התוצאה של תהליך זה היא שמקדם השבירה של האור בחומר תלוי בעוצמת האור הפוגע.
תהליכים לא ליניאריים נוספים הם תהליכים של יצירת הרמוניות גבוהות. משיקולי סימטריה, כל מספר אי-זוגי של פוטונים יכול להיבלע בו-זמנית, וכך ניתן להמיר מספר רב של פוטונים לפוטון אחד בעל אנרגיה השווה לסך האנרגיות של הפוטונים הנבלעים. באופן עקרוני, ככל שמעורבים בתהליך יותר פוטונים, כך ההסתברות לתהליך קטנה יותר, ולכן, כדי ליצור הרמוניות גבוהות יותר ויותר, יש להשתמש בעוצמת אור גבוהה מאוד. אולם, בסוף שנות ה-80 של המאה ה-20 התגלה כי באור בעל עוצמה גדולה מאוד ניתן ליצור, באופן פשוט יחסית, הרמוניות גבוהות מאוד, כתוצאה מתהליך שבו הפוטונים מייננים את האטומים, מאיצים את האלקטרונים וגורמים להם להתנגש שוב באטום - ולפלוט את כל האנרגיה שהאלקטרונים צברו. תהליך זה משמש, בין השאר, לייצור של פולסים קצרים במיוחד של לייזר, שנמשכים כמה עשרות אטו-שניות בודדות (1 אטו-שנייה = 10−18 שניות).
פליטה מאולצת וספונטנית[עריכת קוד מקור | עריכה]
 ערך מורחב – משוואות הקצב של איינשטיין
ערך מורחב – משוואות הקצב של איינשטיין
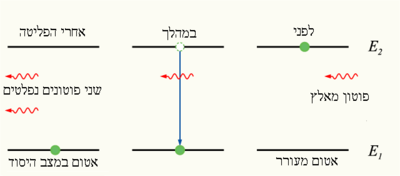
ב-1916 הראה איינשטיין כי מחוק פלאנק עולה קשר בין התדירויות שבהן אטומים פולטים וקולטים פוטונים. מצב זה נובע מההנחה כי האור נפלט ונבלע על ידי אטומים בצורה בלתי תלויה, וכן כי באינטראקציות עם האטומים נשמר שיווי המשקל התרמודינמי. בחלל הנמצא בשיווי משקל תרמודינמי ומכיל קרינה אלקטרומגנטית ואטומים שיכולים לפלוט ולקלוט את הקרינה, דורש שיווי המשקל התרמודינמי כי מספר הפוטונים ליחידת נפח בעלי תדירות יהיה קבוע לאורך זמן. מכאן, קצב הפליטה של פוטונים בתדירות זו חייב להיות שווה לקצב הקליטה שלהם.
איינשטיין שיער כי הקצב שבו המערכת קולטת פוטון בתדירות ועוברת מרמת אנרגיה נמוכה לרמת אנרגיה גבוהה יותר הוא יחסי למספר של המולקולות עם אנרגיה והמספר ליחידת נפח של פוטונים בתדירות זו המקיפים אותן, כך שמתקיימת הנוסחה הבאה:
כאשר הוא קבוע הקצב של הקליטה.
איינשטיין שיער גם, בתעוזה רבה יותר, כי הקצב ההפוך , שבו המערכת פולטת פוטון בתדירות ועוברת מרמת אנרגיה גבוהה לרמת אנרגיה נמוכה יותר מורכב משני ביטויים:
כאשר הוא קבוע הקצב של פליטת פוטון בצורה ספונטנית, ו- הוא קבוע הקצב של פליטת פוטון בתגובה לפוטונים שבסביבה (פליטה מאולצת).
המודל הקינטי הפשוט שתיאר איינשטיין נתן תמריץ משמעותי למחקר, מאחר שהוא היה הפרשנות הסטטיסטית הראשונה לאירועים קוונטים שמעורבים בהם חלקיקים בודדים. איינשטיין הצליח להראות כי , כלומר קבועי הקצב של פליטה וקליטה מאולצת, הם שווים. בנוסף, הוא הראה כי
איינשטיין לא יכול היה להצדיק את משוואות הקצב שלו בצורה מלאה, מאחר שאת ו- היה ניתן לגזור אך ורק ממה שהוא כינה "התאמה של מכניקה ואלקטרודינמיקה להנחה הקוונטית". במכניקת הקוונטים, היחסים בין קבועי הקצב הם תוצאה של הצורה הפשוטה של אברי המטריצה למיקום ולתנע של מתנד הרמוני, מאחר שהשדה האלקטרומגנטי הוא אוסף של מתנדים הרמוניים.
פול דיראק הסיק את קבוע הקצב ב-1926 באמצעות שימוש במודל "חצי-קלאסי", וב-1927 הסיק את כל קבועי הקצב מעקרונות ראשוניים. עבודתו של דיראק היוותה את היסוד לאלקטרודינמיקה הקוונטית, שהיא הקוונטיזציה של השדה המגנטי. הגישה של דיראק נקראת גם "קוונטיזציה שנייה" או תורת השדות הקוונטית. הטיפולים המוקדמים יותר התייחסו רק אל החלקיקים החומריים כקוונטים, ולא לשדה האלקטרומגנטי עצמו.
איינשטיין הוטרד מהעובדה כי התאוריה שלו נראתה בלתי שלמה, מאחר שהיא לא קבעה את כיוון תנועתם של הפוטונים הנפלטים באופן ספונטני. טבעה ההסתברותי של תנועת חלקיקי האור שוער לראשונה על ידי אייזק ניוטון במסגרת טיפולו בשבירה כפולה, ובאופן כללי יותר, בפיצול קרני האור במשטחים לקרן פוגעת ולקרן מוחזרת. ניוטון הניח כי משתנים חבויים בחלקיק האור קובעים את מסלולו. בדומה, איינשטיין קיווה לתאוריה שלמה יותר שלא תשאיר מקום למקריות, ומשום כך סירב לקבל את מכניקת הקוונטים ובהדרגה הפסיק לעבוד עליה. באופן אירוני, הפרשנות ההסתברותית של פונקציית הגל, שפיתח מקס בורן, קיבלה את השראתה מחיפושיו המאוחרים יותר של איינשטיין אחר תאוריה שלמה יותר, ובאופן ספציפי יותר, מניסיונותיו לבנות תאוריית "שדה-רפאים" שבה פוטונים נקודתיים מונחים בצורה הסתברותית על ידי שדות-רפאים הפועלים לפי משוואות מקסוול.
הלייזר[עריכת קוד מקור | עריכה]
 ערך מורחב – לייזר
ערך מורחב – לייזר
גילויו של מנגנון הפליטה המאולצת על ידי איינשטיין הוביל לרעיון לפיו ניתן לבצע הגברה של אור. בתהליך הפליטה המאולצת, גורם פוטון אחד להיווצרותו של פוטון נוסף, וכך נוצרת הכפלה של אור. רעיון זה עומד בבסיס אחת ההמצאות הטכנולוגיות החשובות של המאה ה-20, הלייזר.
הלייזר מבוסס על ייצור של היפוך אוכלוסין - מצב שבו רוב האטומים נמצאים במצב מעורר. באופן זה, כשפוטון פוגע באחד מהאטומים הוא מוכפל כתוצאה מפליטה מאולצת. הפוטונים המתקבלים מוכפלים אף הם, וכך הלאה. כאשר תהליך זה מתבצע בתוך מהוד אופטי[ו] מתקבלת כמות עצומה של פוטונים, שנמצאים באותו מצב קוונטי (בעלי אותו אורך גל, אותו קיטוב ואותו כיוון). תגלית זו זכתה למספר רב של יישומים טכנולוגיים הכוללים צייני לייזר, מכשירי ריתוך בלייזר, תקשורת אופטית, ועוד.
הלייזר הביא לפריצת דרך באופטיקה ולייסוד האופטיקה המודרנית.
קוונטיזציה שנייה[עריכת קוד מקור | עריכה]
ב-1910 הראה פטר דביי כי ניתן להסיק את חוק פלאנק לקרינת גוף שחור מתוך הנחה פשוטה למדי. הוא פירק את השדה האלקטרומגנטי בתוך חלל לאופני תנודה עצמיים, והניח כי האנרגיה בכל אופן תנודה היא כפולה שלמה של hν, כאשר ν היא התדירות. חוק פלאנק לקרינת גוף שחור נובע מיד כסכום גאומטרי. למרות זאת, הגישה של דביי לא הצליחה להניב את הנוסחה הנכונה לשינויים באנרגיה של קרינת גוף שחור, אותה גילה איינשטיין שנה קודם לכן.
ב-1925 נתנו בורן, הייזנברג ויורדן פרשנות חדשה וחשובה לרעיון של דביי. כפי שניתן להראות באמצעות התאוריה הקלאסית, אופני התנודה של השדה האלקטרומגנטי - קבוצה שלמה של גלים מישוריים המסומנים לפי וקטור הגל k ומצב הקיטוב שלהם - שקולים לקבוצה של מתנדים הרמוניים פשוטים חופשיים. בתאוריה הקוונטית, רמות האנרגיה של המתנדים הן E = nhν, כאשר ν היא תדירות המתנד. החידוש העיקרי היה בזיהוי של אופן תנודה אלקטרומגנטי בעל אנרגיה E = nhν כמצב ובו n פוטונים, כל אחד מהם בעל אנרגיה hν. גישה זו מניבה את הנוסחה הנכונה לשינויים באנרגיה.
דיראק עשה צעד נוסף קדימה: הוא התייחס לאינטראקציה בין מטען ושדה אלקטרומגנטי כהפרעה קטנה אשר גורמת לשינויים במצבי הפוטונים ובמספר הפוטונים באופן התנודה, אך משמרת את האנרגיה והתנע הכולל. כאמור בסעיף הקודם, דיראק הסיק את קבועי הקצב ו- של איינשטיין מעקרונות ראשוניים, והראה כי התפלגות בוז-איינשטיין של הפוטונים היא תוצאה טבעית של קוונטיזציה נכונה של השדה האלקטרומגנטי. גישה זו היא הפוכה לזו של בוז עצמו, אשר קיבל את חוק פלאנק לקרינת גוף שחור מתוך התפלגות בוז-איינשטיין (ולא להפך). בזמנו של דיראק, עדיין לא היה ידוע כי כל הבוזונים, ולא רק הפוטונים, חייבים לציית להתפלגות בוז-איינשטיין.
תורת ההפרעות מסדר שני של דיראק עשויה לכלול פוטונים וירטואליים - מצבי-ביניים ארעיים של השדה האלקטרומגנטי. הפוטונים הווירטואליים מתווכים באינטראקציות החשמליות והמגנטיות הסטטיות. בתורות קוונטיות של השדות כגון אלה, אמפליטודת ההסתברות של אירועים נצפים מחושבת על ידי חיבור כל מצבי-הביניים האפשריים, אפילו אלה שאינם פיזיקליים. מכאן, פוטונים וירטואליים אינם מוכרחים לקיים את הנוסחה E = pc, ועשויים להיות להם מצבי קיטוב נוספים: שלושה או ארבעה מצבים כאלה (תלוי בכיול), במקום שניים בלבד בפוטונים אמיתיים. אף על פי שהפוטונים הווירטואליים אינם ברי-גילוי בניסוי, הם תורמים במידת-מה להסתברויות של אירועים. למעשה, חישובים הפרעתיים מסדר שני וגבוה יותר עשויים לתרום במידה אינסופית לסכום, ובכך לגרום לתוצאות שאינן פיזיקליות אשר ניתן לתקנן באמצעות רנורמליזציה. חלקיקים וירטואליים נוספים עשויים לתרום לסכום גם הם: לדוגמה, שני פוטונים עשויים לקיים אינטראקציה ביניהם באמצעות זוגות וירטואליים של אלקטרון ופוזיטרון. המילה "וירטואליים" מציינת כי החלקיקים מתאיינים לאחר פרק זמן קצר מספיק על-מנת שעקרון אי הוודאות "יפצה" על ההפרה של חוקי שימור האנרגיה והתנע.
בסימון מודרני, המצב הקוונטי של שדה אלקטרומגנטי נכתב כמכפלה טנזורית של המצבים של כל אחד מאופני התנודה האלקטרומגנטים:
כאשר מייצג את המצב בו פוטונים נמצאים באופן תנודה . בסימון זה, יצירתו של פוטון חדש (למשל פליטתו בעת מעבר אנרגיה באטום) באופן תנודה נכתב בצורה . הסימון נועד לבטא את הרעיון של בורן, הייזנברג ויורדן שצוין לעיל, ואינו מחדש שום דבר מבחינה פיזיקלית.
שזירה: פוטונים כנושאי מידע קוונטי[עריכת קוד מקור | עריכה]
היתרון הגדול של הפורמליזם של הקוונטיזציה השנייה הוא, שהיא מאפשרת להתייחס בצורה נכונה לשזירה בין פוטונים. על פי תורת הקוונטים חלקיקים יכולים להיות במצבים שזורים (entangled) – כלומר, מקרים בהם מצב של חלקיק אחד תלוי במצב של חלקיקים אחרים, ומדידה של אחד מהם משפיעה על המצב של האחרים. דוגמה למצב כזה הוא מצב שבו שני פוטונים נמצאים בסופרפוזיציה קוונטית של שני מצבים: מצב בו שניהם בקיטוב מאונך, ומצב בו שניהם נמצאים בקיטוב מאוזן. מצב זה מסומן בקוונטיזציה שנייה באופן הבא:
כאשר 0 או 1 מציינים קיטוב אופקי או אנכי, ו-A,B מציינים את שני הפוטונים. כאשר שני פוטונים נמצאים במצב כזה, אזי במדידה של הקיטוב של כל אחד מהם יש סיכוי של חצי שהקיטוב יהיה אופקי או מקביל, אבל במקרה שהקיטוב של אחד נמדד כאנכי אזי בהכרח הקיטוב של השני גם הוא יהיה אנכי.
האופטיקה הקוונטית היא תחום מחקר בפיזיקה החוקר את תכונות השיזור בין הפוטונים. ישנם מספר שיטות ניסיוניות המאפשרות ליצור זוגות של פוטונים שזורים, שהמקובלת ביותר מביניהם היא על ידי שימוש בהמרה אופטית כלפי מטה (optical down conversion). בתהליך זה פוטון העובר דרך גביש נבלע ונפלטים שני פוטונים אשר סכום האנרגיות שלהם שווה לאנרגיה של הפוטון המקורי. הפוטונים המתקבלים שזורים זה בזה.
אופטיקה קוונטית הועלתה גם כאפשרות ליישום מערכות של חישובים קוונטיים. תחום המידע הקוונטי והחישובים הקוונטיים החל ברעיון של ריצ'רד פיינמן לפיו ביצוע של חישובים במערכות שזורות, דומה לביצוע מספר רב של חישובים במקביל. בעקבות רעיון זה נמצאו אכן במהרה מספר אלגוריתמים המאפשרים ביצוע פעולות חישוב בעזרת חישובים קוונטיים, בצורה מהירה הרבה יותר מאשר חישובים במחשבים קלאסיים - כולל אלגוריתם לפירוק מהיר של מספר לרכיבים ראשוניים. בעקבות עבודות תאורטיות אלו החל מאמץ גדול ליישם מחשבים קוונטיים, והועלו מספר רב של מערכות כמועמדים למחשבים קוונטיים הכוללות MRI, מלכודות יונים, נקודות קוונטיות (quantum dots) וכן שיטות אופטיות. רעיונות אחרים הנוגעים לשימושים במידע קוונטי הם הצפנה קוונטית וטלפורטציה. הצפנה קוונטית מסתמכת על כך שבתורת הקוונטים, מדידה משפיעה על המצב של מערכת. על בסיס הרעיון הזה הומצאו פרוטוקולים של התקשרות באמצעות מידע קוונטי המבטיחים שאם גורם כלשהו מנסה להאזין להתקשרות, ניתן יהיה להבחין בכך. טלפורטציה קוונטית, שמקורה בפרדוקס EPR (איינשטיין פודולסקי רוזן) מקורה ברעיון לפיו ניתן ליצור חלקיקים השזורים זה בזה ולהביא אותם למרחק רב זה מזה, ולאחר מכן ביצוע פעולות על אחד מהם ישפיע גם על השני. בדרך זו ניתן, תאורטית, להעביר אינפורמציה על פני מרחקים גדולים במהירות רבה.
יתרונם של פוטונים כנושאי מידע קוונטי הוא בכך שהאינטראקציה בינם לסביבה קטנה ביותר, ומשום כך מידע קוונטי המאוחסן בפוטונים יהיה עמיד מאוד לרעש (decoherence). משום כך פוטונים נחשבים ככלי מועדף להעברה של מידע קוונטי על פני מרחקים גדולים, דבר הנחוץ בשביל תקשורת קוונטית ובשביל טלפורטציה קוונטית. אך יתרון זה הוא גם חיסרון: מכיוון שהאינטראקציה בין פוטונים לבין הסביבה קטנה מאוד, קשה מאוד לבצע על פוטונים פעולות חישוב, וכן קשה מאוד לייצר מצבים בהם מספר רב של פוטונים שזורים.
הפוטון כבוזון כיול[עריכת קוד מקור | עריכה]
את השדה האלקטרומגנטי ניתן להבין כשדה כיול, כלומר שדה הנובע מהדרישה לסימטריה בלתי-תלויה בכל נקודה במרחב-זמן. סימטריית הכיול של השדה האלקטרומגנטי היא סימטריית U(1) אבלית של מספר מרוכב, אשר משקפת את היכולת לשנות את המופע של מספר מרוכב בלי לשנות את המספר הממשי הנובע ממנו, כגון אנרגיה או הלגראנז'יאן.
הערכים הקטנים ביותר של שדה כיול אבלי חייבים להיות בוזונים חסרי מסה ומטען, כל עוד הסימטריה אינה שבורה; מכאן נוכל להסיק כי הפוטון יהיה חסר מסה, בעל מטען חשמלי אפס וספין שלם. במקרה הספציפי של הכוח האלקטרומגנטי, לפוטון צריך להיות ספין ±1, ולכן הרכיב שלו שנמדד בכיוון התנועה חייב להיות . שתי האפשרויות (פלוס ומינוס) מתאימות לשני מצבי הקיטוב המעגלי של הפוטון (ימני ושמאלי). לפוטונים הווירטואליים (אשר תוארו בסעיף הקודם) עשויים להיות מצבי קיטוב נוספים, לא-פיזיקליים.
במודל הסטנדרטי של פיזיקת החלקיקים, הפוטון הוא אחד מארבעה בוזוני הכיול של הכוח האלקטרו-חלש. השלושה האחרים מסומנים W+, W- ו-Z0 והם אחראים לפעולתו של הכוח החלש. שלא כמו הפוטון, לבוזוני הכיול האחרים יש מסת מנוחה, מכיוון שסימטריית הכיול SU(2) שלהם שבורה. איחוד הפוטון עם בוזוני הכיול W ו-Z במסגרת הכוח האלקטרו-חלש בוצע על ידי שלדון לי גלשאו, עבדוס סלאם וסטיבן ויינברג, ובזכותו הם קיבלו את פרס נובל לפיזיקה ב-1979. הפיזיקאים ממשיכים לנסות למצוא תאוריה מאוחדת גדולה אשר תאחד בין ארבעת בוזוני הכיול המוזכרים לעיל לבין שמונת הגלואונים המתוארים בכרומודינמיקה הקוונטית - אך ניבויים חשובים של התאוריות הללו, כגון התפרקות פרוטון, לא נצפו בניסוי.
תרומות למסה של מערכת[עריכת קוד מקור | עריכה]
מערכת הפולטת פוטון מאבדת כמות אנרגיה השווה לאנרגיה E של הפוטון, כפי שנמדדה במערכת הייחוס שבה נמצאת המערכת הפולטת במנוחה. איבוד האנרגיה שקול לאיבוד מסה בכמות E / c2. בדומה, בליעת פוטון שקולה לרכישת מסה בכמות מתאימה.
קונספט זה מעורב בתחזית חשובה של האלקטרודינמיקה הקוונטית. התאוריה מצליחה לחזות את מומנט הדיפול המגנטי של לפטונים ברמת דיוק גבוהה במיוחד; מדידות ניסיוניות של מומנט הדיפול המגנטי תאמו את התחזיות בצורה מושלמת. התחזיות דורשות להביא בחשבון את התרומה של פוטונים וירטואליים למסה של הלפטון. דוגמה נוספת לתרומה כזו אשר אושרה בניסוי היא הסחת לם אשר נצפה במבנה העל-דק של זוגות לפטונים קשורים, כגון מיואוניום (אטום אקזוטי המורכב מאנטי-מיואון ואלקטרון) ופוזיטרוניום (אטום אקזוטי המורכב מאלקטרון ופוזיטרון).
מאחר שפוטונים תורמים לטנזור המאמץ והאנרגיה, הם מפעילים משיכה כבידתית על עצמים אחרים, לפי תורת היחסות הכללית. גם להפך, הפוטונים עצמם מושפעים מהכבידה; מסלוליהם, הישרים בדרך כלל, עשויים להתעקם על ידי מרחב-זמן מעוקם (עובדה ששימשה כהוכחה הראשונה לנכונותה של תורת היחסות הכללית), תופעה הבאה לידי ביטוי בעידוש כבידתי. כמו כן, תדירותם עשויה להפוך נמוכה יותר (לעבור הסחה לאדום) על ידי מעבר לפוטנציאל כבידתי גבוה יותר, כגון בניסוי פאונד-רבקה. אפקטים אלו אינם ייחודיים למודל הפוטונים; אותם אפקטים בדיוק נחזים על ידי המודל הקלאסי של גל אלקטרומגנטי.
פוטונים בחומר[עריכת קוד מקור | עריכה]

אור שעובר דרך חומר שקוף נע במהירות נמוכה ממהירות האור בריק. לדוגמה, פוטונים חווים התנגשויות רבות כל כך בדרכם מליבת השמש, שעשויות לעבור מיליון שנה עד שהם יגיעו אל פני השטח; אך ברגע שהם הגיעו לחלל הפתוח, הם יעברו את המרחק עד כדור הארץ ב-8.3 דקות בלבד. הגורם בו מוקטנת המהירות נקרא מקדם השבירה של החומר. לפי מודל הגל הקלאסי, ניתן להסביר את ההאטה בכך שהאור יוצר קיטוב חשמלי בחומר, החומר המקוטב מקרין אור חדש, והאור החדש יוצר התאבכות עם גל האור הישן וגורם לעיכובו. הסבר נוסף הוא שבתור קרינה אלקטרומגנטית, מהירות התפשטותו של גל האור נתונה על ידי משוואות מקסוול: כאשר הוא המקדם הדיאלקטרי ו- הוא מקדם הפרמביליות. בחומר, מקדמים אלה שונים מערכם בוואקום, ולכן מהירות הפוטון שונה. במודל החלקיקי, ניתן לתאר את ההאטה כערבוב של הפוטון עם עירורים קוונטים של החומר (דמוי-חלקיקים כגון פונונים ואקסיטונים) ליצירת פולריטון; לפולריטון יש מסה אפקטיבית שונה מאפס, ולכן אינו יכול לנוע במהירות c. אור בתדירויות שונות עשוי לנוע בחומר במהירויות שונות; אפקט זה נקרא נפיצה. מהירות ההתפשטות של הפולריטון, , זהה למהירות החבורה שלו, שהיא הנגזרת של האנרגיה לפי התנע:
כאשר ו- הם האנרגיה וגודל התנע של הפולריטון, ו- ו- הם התדירות הזוויתית ומספר הגל בהתאמה. במקרים מסוימים, הנפיצה עשויה לגרום לאור לנוע במהירות איטית מאוד בחומר. בתוצאות האינטראקציה של הפוטון עם דמוי-חלקיקים אחרים ניתן לצפות באופן ישיר בתהליכי פיזור רמן ופיזור ברילואי.
פוטונים עשויים להיבלע על ידי אלקטרונים באטומים ובמולקולות, ולגרום לשינויים ברמות האנרגיה שלהם. דוגמה קלאסית לכך היא התהליך המולקולרי ברטינל (C20H28O, ראו תמונה משמאל), המולקולה שאחראית על הראייה. תהליך זה נתגלה ב-1958 על ידי הביוכימאי זוכה פרס נובל ג'ורג' ואלד ועמיתיו. כפי שניתן לראות, בליעת הפוטון גורמת לאיזומריות ציס-טראנס אשר, בשילוב עם תהליכים אחרים, מתורגמת לאותות עצביים. בליעת הפוטונים עשויה אפילו לפרק קשרים כימיים, למשל בפוטוליזה של כלור; בתהליכים כאלה עוסקת הפוטוכימיה.
יישומים טכנולוגיים[עריכת קוד מקור | עריכה]
לפוטונים יישומים רבים בטכנולוגיה. בדוגמאות שלהלן נבחרו יישומים של מודל הפוטונים עצמו, ולא יישומים אופטיים כלליים שהיו מתאימים גם למודל הגלי הקלאסי. הלייזר הוא דוגמה ליישום חשוב במיוחד (ראו למעלה).
בפוטונים בודדים ניתן להבחין באמצעות מספר שיטות. שפופרת מכפילת אור מנצלת את האפקט הפוטואלקטרי: פוטון שפוגע בלוח מתכת פולט אלקטרון, וגורם לתגובת שרשרת גוברת והולכת של אלקטרונים. שבבי CCD משתמשים באפקט דומה במוליכים למחצה: פוטון מייצר מטען שניתן לגלותו על קבל מיקרוסקופי. גלאים אחרים כגון מונה גייגר משתמשים ביכולת של פוטון ליינן מולקולות גז, וכך לגרום לשינוי במוליכות שניתן להבחין בו.
נוסחת פלאנק-איינשטיין, E = hν, משמשת לעיתים קרובות מהנדסים וכימאים, גם על מנת לחשב את השינוי באנרגיה כתוצאה מבליעת פוטון וגם כדי לחזות את תדירות האור שנפלט ממעבר אנרגיה מסוים. לדוגמה, את ספקטרום הפליטה של נורת פלואורסצנט ניתן לקבוע על ידי שימוש במולקולות גז בעלות רמות אנרגיה שונות, והתאמת האנרגיה הטיפוסית של האלקטרונים הפוגעים במולקולות הגז שבתוך הנורה.
בתנאים מסוימים, אף על פי שלפוטון יחיד אין מספיק אנרגיה כדי לעורר מעבר אנרגיה, ניתן לעשות זאת באמצעות שני פוטונים כאלה. שיטה זו מאפשרת מיקרוסקופיה בהפרדה גבוהה, מאחר שהדגימה בולעת אנרגיה רק באזורים בהם שתי קרניים מצבעים שונים חופפות בצורה משמעותית, ואזור החפיפה עשוי להיות קטן בהרבה מאזור הפגיעה של קרן יחידה (ראו מיקרוסקופ דו-פוטוני). יתרון נוסף הוא ששני הפוטונים גורמים פחות נזק לדגימה, מאחר שהם בעלי אנרגיה קטנה יותר בהשוואה לפוטון יחיד.
ישנם מקרים בהם שני מעברי אנרגיה עשויים להיקשר כך שבעוד מערכת אחת קולטת פוטון, מערכת אחרת "גונבת" את האנרגיה שלו ופולטת מחדש פוטון בתדירות שונה. זהו הבסיס לשיטת העברת אנרגיה לפי פרסטר אשר משמשת למדידת מרחקים ברמה המולקולרית.
מחקר נוכחי[עריכת קוד מקור | עריכה]
כיום סבורים שטבעו היסודי של הפוטון ידוע ומובן מבחינה תאורטית: לפי המודל הסטנדרטי, הפוטון הוא בוזון כיול בעל ספין 1, ללא מסה וללא מטען, הנובע מסימטריית הכיול U(1) ומתווך באינטראקציות אלקטרומגנטיות. למרות זאת, הפיזיקאים ממשיכים לחפש אי-התאמות בין התאוריה והניסוי, בתקווה למצוא רמזים לתאוריות אפשריות אשר ירחיבו את המודל הסטנדרטי. בפרט, פיזיקאים ניסיוניים ממשיכים להגדיר גבולות עליונים טובים יותר ויותר למטען והמסה של הפוטון: אם יתגלה ערך שונה מאפס לאחד מהערכים האלו, תהא זו הפרה חמורה של המודל הסטנדרטי. בכל זאת, כל המידע הניסיוני שנאסף עד עתה מצביע על כך שלפוטון מטען ומסה אפס. הגבולות העליונים המקובלים כיום למטען ולמסה של הפוטון הם 5×10−52 קולון (או 3×10−33 כפול המטען האלמנטרי) ו-1.1×10−52 קילוגרם (או 1×10−22 כפול מסת האלקטרון), בהתאמה.
מחקר רב נערך בנושא היישום של פוטונים באופטיקה קוונטית. פוטונים הם מועמדים מתאימים לתפקיד הגורמים במחשב קוונטי, ושזירה קוונטית בפוטונים היא מוקד למחקר רב. אופטיקה לא ליניארית היא תחום מחקר פעיל נוסף, ובו נושאים כגון קליטה דו-פוטונית, מודולציית מופע עצמית ומתנד פרמטרי אופטי. למרות זאת, תהליכים כאלה בדרך כלל אינם דורשים את הנחת קיומם של הפוטונים כשלעצמה; לעיתים קרובות ניתן להסביר אותם באמצעות התייחסות לאטומים כאל מתנדים לא ליניארים. התהליך הלא-ליניארי של המרת SPDC משמש לעיתים קרובות ליצירת מצבים של פוטון יחיד. לבסוף, פוטונים הם חיוניים בהיבטים מסוימים של תקשורת אופטית, ובמיוחד הצפנה קוונטית.
לקריאה נוספת[עריכת קוד מקור | עריכה]
- פרופ' קירש יורם, בן-יעקב מיכל, יסודות הפיזיקה ב (כרך 7), האוניברסיטה הפתוחה, 1998
- Clauser, JF. (1974). "Experimental distinction between the quantum and classical field-theoretic predictions for the photoelectric effect". Phys. Rev. D. 9: 853–860. doi:10.1103/PhysRevD.9.853.
- Kimble, HJ; Dagenais M.; Mandel L. (1977). "Photon Anti-bunching in Resonance Fluorescence". Phys. Rev. Lett. 39: 691–695. doi:10.1103/PhysRevLett.39.691.
- Grangier, P; Roger G.; Aspect A. (1986). "Experimental Evidence for a Photon Anticorrelation Effect on a Beam Splitter: A New Light on Single-Photon Interferences". Europhysics Letters. 1: 501–504. doi:10.1209/0295-5075/1/4/004.
- Thorn, JJ; Neel MS; Donato VW; Bergreen GS; Davies RE; Beck M. (2004). "Observing the quantum behavior of light in an undergraduate laboratory". American Journal of Physics. 72: 1210–1219. doi:10.1119/1.1737397.
- Proof of the Existence of Photons (the Grangier Experiment)
- Pais, A. (1982). Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford University Press.
- "Roy Glauber's Nobel Lecture, "100 Years of Light Quanta"".
- Lamb, WE (1995). "Anti-photon". Applied Physics B. 60: 77–84. doi:10.1007/BF01135846.
- Special supplemental issue of Optics and Photonics News (vol. 14, October 2003)
- Roychoudhuri, C; Rajarshi R. "The nature of light: what is a photon?". Optics and Photonics News. 14: S1 (Supplement).
- Zajonc, A. "Light reconsidered". Optics and Photonics News. 14: S2–S5 (Supplement).
- Loudon, R. "What is a photon?". Optics and Photonics News. 14: S6–S11 (Supplement).
- Finkelstein, D. "What is a photon?". Optics and Photonics News. 14: S12–S17 (Supplement).
- Muthukrishnan, A; Scully MO; Zubairy MS. "The concept of the photon—revisited". Optics and Photonics News. 14: S18–S27 (Supplement).
- Mack, H; Schleich WP. "A photon viewed from Wigner phase space". Optics and Photonics News. 14: S28–S35 (Supplement).
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- ארז גרטי, חלקיקי החומר – הפוטון, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 4 ביולי 2011
- פוטון, באתר אנציקלופדיה בריטניקה (באנגלית)
 פוטונים, דף שער בספרייה הלאומית
פוטונים, דף שער בספרייה הלאומית
ביאורים[עריכת קוד מקור | עריכה]
- ^ ההסבר של האפקט הפוטואלקטרי על ידי אלברט איינשטיין נחשב לגילוי הפוטון.
- ^ הביטוי מייצג את אנרגיית הפוטון, כאשר h הוא קבוע פלאנק והאות היוונית ν (נו) היא תדר הקרינה. לעיתים מסומן הפוטון גם hf, כאשר f מסמלת את התדר.
- ^ מסת הפוטון נחשבה לאפס בדיוק, בהתבסס על ניסויים והתחשבויות תאורטיות המתוארים בגוף הערך. מספר מקורות מציינים גם את רעיון ה"מסה היחסותית", שהיא רק סקאלת האנרגיה ליחידות מסה. עבור פוטון עם אורך גל λ או אנרגיה E, יהיה הדבר שווה ל-h/λc או E/c^2. שימוש זה במושג "מסה" אינו מקובל יותר בספרות הפיזיקה.
- ^ להבדיל מפרמיונים, כמו אלקטרונים, ששניים מהם לא יכולים להיות באותו מצב קוונטי. כך, למשל, אין הם יכולים להיות בעלי אותו ספין ובאותו אורביטל בעת ובעונה אחת (לא חשוב אם האורביטל הוא אורביטל אטומי או מולקולרי).
- ^ ארבע תנע הוא ההכללה של התנע התלת־ממדי הרגיל לארבעת הממדים של היקום לפי תורת היחסות, המכונים יחדיו המרחב-זמן. מכיוון שהתנע הוא וקטור במרחב, הוא ארבע וקטור במרחב-זמן.
- ^ מהוד אופטי הוא מתקן ובו שתי מראות, אשר דרך אחת מהן יש אפשרות לחלק קטן מהפוטונים להימלט. מרחקן של המראות זו מזו מתאים לאורך הגל הרצוי. רוב הפוטונים נעים הלוך ושוב בתוך המהוד, כך שהם יכולים לגרום לעוד ועוד פליטות מאולצות. הפוטונים שנמלטים דרך אחת המראות הם אלה שיוצרים את קרן הלייזר.
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Wave-Particle Duality , אתר hyperphysics
- ^ אפקט קומפטון, אנציקלופדיה בריטניקה
- ^ יצירת זוג, אנציקלופדיה בריטניקה
- ^ Why do electrons emit radiation?, אתר physics.stackexchange
- ^ Historians still call the year 1905 the annus mirabilis, אתר hyperhistory
- ^ Albert Einstein und das Lichtquantum, מאמרו של מקס בורן מ-1955 (גרמנית)
- ^ The Conservation of Photons, מאמרו של לואיס מ-1926
- ^ Light through the ages: Ancient Greece to Maxwell, אתר groups.dc
- ^ Physics: Light 1.a Introduction, Ancient History of theories of light, אתר web.stanford.edu
- ^ דואליו גל-חלקיק, אתר photonterrace.net
- ^ Gauge boson exchange , אתר hep.ucl.ac.uk











































































