גרדיאנט

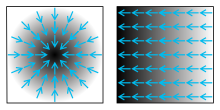
המחשה של גרדיאנט. באיורים האלה, השדה הסקלרי מתואר באמצעות שינוי הצבע, כאשר אזורים כהים יותר הם ערכים גדולים יותר של הפונקציה. החצים הכחולים מתארים את הגרדיאנט הנגזר מהשדה הסקלרי. החצים פונים אל עבר האזורים הגבוהים יותר.

בחשבון אינפיניטסימלי של מספר משתנים, גרדיאנט הינו אופרטור וקטורי המופעל על שדה סקלרי.
הגרדיאנט של שדה סקלרי הוא שדה וקטורי המשייך לכל נקודה במרחב וקטור המצביע אל הכיוון בו השינוי בשדה הסקלרי מקסימלי (חיובי), ואשר גודלו כשיעור השינוי המקסימלי.

אינטואיציה

נתבונן לדוגמה באזור הררי. הגובה של כל נקודה יתואר על ידי פונקציה (שדה סקלרי). בכל נקודה ניתן להסתכל על הכיוון בו השיפוע לפונקציה זו הוא הגדול ביותר (זהו הכיוון בו הגובה משתנה בצורה החזקה ביותר. אם נשחרר כדור בנקודה זו הכדור יתגלגל בדיוק לכיוון ההפוך). באופן זה ניתן להתאים לכל נקודה וקטור שכיוונו הוא כיוון השיפוע הגדול ביותר וגודלו נקבע על פי גודל שיפוע זה. וקטור זה הוא וקטור הגרדיאנט.

סימון

אם $\ f$ פונקציה סקלרית והגרדיאנט שלה הוא פונקציה וקטורית $\vec F$, נסמן:

$\vec F = \operatorname{grad} \ f = \nabla \ f = \vec \nabla \ f$

כאשר $\vec{\nabla}$ מסמל את אופרטור הגזירה דֶל (סמל המשולש עצמו נקרא בשם "נבלה") המוגדר כווקטור של נגזרות חלקיות, כלומר:

$\vec{\nabla} \equiv \hat{x}\frac{\partial}{\partial x} +\hat{y} \frac{\partial}{\partial y } + \hat{z}\frac{\partial}{\partial z} \equiv \left( \ \partial_x \ , \ \partial_y \ , \ \partial_z \right)$

הגדרה פורמלית במרחב האוקלידי התלת ממדי

במרחב אוקלידי תלת ממדי, הגרדיאנט של שדה סקלרי כלשהו שמתואר על ידי קואורדינטות קרטזיות $\ \psi(x,y,z)$ מוגדר כך:

$\vec{\nabla} \psi(x,y,z) \equiv \frac{\partial \psi(x,y,z)}{\partial x}\hat{x} + \frac{\partial \psi(x,y,z)}{\partial y}\hat{y} + \frac{\partial \psi(x,y,z)}{\partial z}\hat{z}$

כאשר $\{\hat{x}, \hat{y}, \hat{z}\}$ הינם וקטורי היחידה המקבילים לצירים.

באופן כללי, עבור $\ f$ פונקציה סקלרית כלשהי מעל מרחב וקטורי בעל $\ n$ ממדים, ניתן להגדיר את הגרדיאנט כך:

$\operatorname{grad}f(a) \equiv \left( \frac{\partial f}{\partial x_1}(a), \frac{\partial f}{\partial x_2}(a), \dots , \frac{\partial f}{\partial x_n}(a) \right)$

דוגמה

הפוטנציאל הוא שדה סקלרי $\ U(\vec{r})$, והכח שפועל על חלקיק שנמצא בהשראת אנרגיה פוטנציאלית הוא הגרדיאנט של האנרגיה הפוטנציאלית $\ \vec{F}(\vec{r}) = -\vec{\nabla}U(\vec{r})$ (ראה דוגמאות ספציפיות בערך אנרגיה פוטנציאלית). לכן, הכח שיפעל על הגוף ימשוך אותו לכיוון בו הפוטנציאל יקטן הכי הרבה.

דוגמה נוספת (חישובית):

יהי $f(\mathbf{r}) = |\mathbf{r}| = r$ שדה סקלרי (הגזיר בכל מקום פרט ל-$\mathbf{r}=0$). אזי הגרדיאנט שלו (בקואורדינטות קרטזיות) הוא

$\vec{\nabla} f = \frac{\partial r}{\partial x} \hat{\mathbf{e}}_x + \frac{\partial r}{\partial y} \hat{\mathbf{e}}_y + \frac{\partial r}{\partial z} \hat{\mathbf{e}}_z = \frac{ x \hat{\mathbf{e}}_x + y \hat{\mathbf{e}}_y + z \hat{\mathbf{e}}_z }{ \sqrt{ x^2 + y^2 + z^2} } = \frac{\mathbf{r}}{r} = \hat{\mathbf{r}}$

שכן $\frac{\partial}{\partial x} r = \frac{\partial}{\partial x} \sqrt{x^2 + y^2 + z^2} = \frac{2 x}{2 \sqrt{x^2 + y^2 + z^2}}$.
כדאי לשים לב שהחישוב הוא מיידי בקואורדינטות כדוריות, שם הגרדיאנט נתון על ידי הנוסחה

$\vec \nabla f = \frac{\partial f}{\partial r} \hat{\mathbf{r}} + \frac{1}{r}\frac{\partial f}{\partial \theta} \hat{\mathbf{ \theta}} + \frac{1}{r\sin\theta}\frac{\partial f}{\partial \phi} \hat{\mathbf{\phi}}$

ומאחר ש $\frac{\partial r}{\partial \theta} = 0 = \frac{\partial r}{\partial \phi}$ מקבלים ש-

$\vec \nabla f = \frac{\partial f}{\partial r} \hat{\mathbf{r}} = \frac{\partial r}{\partial r} \hat{\mathbf{r}} = \hat{\mathbf{r}}$.

כצפוי, בשתי הדרכים קיבלנו תוצאה זהה.

גרדיאנט באנליזה על יריעות

את הגרדיאנט יותר טבעי להגדיר דווקא כפונקציונל הנקרא "דיפרנציאל":

$\ df = \sum_{\mu} \frac{ \partial f}{ \partial x^\mu} dx^\mu$

פונקציונל זה מקבל וקטור v ומחזיר את הסקלר

$\ ( df ) (\vec{v}) = \lang df , \vec{v} \rang = \sum_{\mu} v^\mu \frac{ \partial f}{ \partial x^\mu}$

האות $\mu$ הכתובה בכתיב עילי מייצגת אינדקס רץ שמייצג קואורדינטה של וקטור ולא חזקה.

במרחב עם מטריקה, אפשר להגדיר את הגרדיאנט כווקטור על ידי "העלאת אינדקסים", כלומר, על ידי התאמת וקטור $\vec{\nabla} f$ ל df כך ש

$\ df( \vec{v} ) = g( \vec{v} , \vec{\nabla} f)$

כאשר g היא המטריקה: תבנית בילינארית סימטרית וחיובית בהחלט.

בקואורדינטות אפשר לכתוב את וקטור הגרדיאנט כך:

$\ \vec{\nabla} f = \sum_{\mu , \nu} g^{\mu \nu} (df)_{\nu} \partial_\mu = \sum_\mu \left( \sum_{\nu} g^{\mu \nu} \frac{ \partial f}{\partial x^\nu} \right) \partial_\mu$

כאשר $g^{\mu \nu}$ הוא האיבר בשורה ה-$\mu$ והעמודה ה--$\nu$ של המטריקה ההפכית (כלומר: המטריצה ההפכית למטריקה, g^-1) ו-$\partial_\mu = \frac{\partial \vec{r} }{\partial x^\mu}$ הם הווקטורים המשיקים הפורשים את המרחב המשיק בנקודה.

גרדיאנט במערכת קואורדינטות אורתוגונליות כלשהי

נניח מערכת קואורדינטות אורתוגונלית $(q_1 , q_2 , q_3)$. כלומר, וקטורי היחידה המתאימים מקיימים

$\hat{\mathbf{e}}_i \cdot \hat{\mathbf{e}}_j = \delta_{ij}$

כאשר

$\delta_{ij} = \begin{cases} 1 & \textrm{ If } \ i=j \\ 0 & \textrm{ If } \ i \neq j \end{cases}$

הוא הדלתא של קרונקר.

הווקטורים המשיקים הם $\frac{\partial \mathbf{r}}{\partial q_i} = h_i \hat{\mathbf{e}}_i$.

נרשום צורה כללית לגרדיאנט של פונקציה סקלרית כלשהי $f$:

$\nabla f = \sum_{i=1}^{3} f_i \hat{\mathbf{e}}_i$

ונמצא את המקדמים $f_1 , f_2 , f_3$.

לשם כך נחשב את הדיפרנציאל של $f$:

$df = \sum_{i=1}^{3} \frac{\partial f}{\partial q_i} dq_i$

מתקיים ש-$df = \nabla f \cdot d\mathbf{r}$ אבל

$d\mathbf{r} = \sum_{i=1}^{3} \frac{\partial \mathbf{r}}{\partial q_i}dq_i = \sum_{i=1}^{3} h_i \hat{\mathbf{e}}_i dq_i$

ולכן, בגלל שווקטורי היחידה המשיקים הם אורתוגונליים $\hat{\mathbf{e}}_i \cdot \hat{\mathbf{e}}_j = \delta_{ij}$ מתקיים

$\sum_{i=1}^{3} \frac{\partial f}{\partial q_i} dq_i = df = \nabla f \cdot d\mathbf{r} = \sum_{i=1}^{3} f_i h_i dq_i$

מכיוון ש-$dq_1, dq_2 , dq_3$ בלתי תלויים נשווה מקדמים איבר איבר ונקבל

$f_i = \frac{1}{h_i} \frac{\partial f}{\partial q_i}$

ומכאן נקבל

$\nabla f= \sum_{i=1}^{3} \frac{1}{h_i} \frac{ \partial f}{\partial q_i} \hat{\mathbf{e}}_i = \frac{1}{h_1} \frac{\partial f}{\partial q^1} \hat{\mathbf{e}}_1+ \frac{1}{h_2} \frac{\partial f}{\partial q^2} \hat{\mathbf{e}}_2 + \frac{1}{h_3} \frac{\partial f}{\partial q^3} \hat{\mathbf{e}}_3$

כנדרש. $\blacksquare$

הערה: ההכללה לממד כלשהו n מיידית. עובדים עם הצגת הסכומים כ-$\Sigma$ ונותנים לכל אינדקס לרוץ מ-1 עד n.

הוכחה המבוססת על גאומטריה דיפרנציאלית

נניח מערכת קואורדינטות אורתוגונלית $(q^1 , q^2 , q^3)$.

הוקטורים המשיקים הם: $\partial_{q^i} = \frac{ \partial \mathbf{r} }{\partial q^i} = h_i \hat{\mathbf{e}}_i$ כאשר $\hat{\mathbf{e}}_i$ הם וקטורים משיקים מנורמלים ו-$h_i$ הם ה-scale factors.

הטנזור המטרי במקרה של קואורדינטות אורתוגונליות

$g = \mbox{diag}(h_1^2 , h_2^2 , h_3^2)$

הוא מטריצה אלכסונית, ונזכור ש-

$\ dq^i = \sum_j g^{ij} \partial_{q^j}$

כאשר $g^{ij} = g^{-1} = \mbox{diag}( 1/h_1^2 , 1/h_2^2 , 1/h_3^2 )$ היא המטריצה ההופכית ל-g.

נציב בהגדרת הגרדיאנט,

$\nabla f = \sum_i \frac{ \partial f}{\partial q^i} dq^i = \sum_{ij} g^{ij} \frac{\partial f}{\partial q^i} \partial_{q^j} = \sum_{ij} \frac{1}{h_i^2} \delta^{ij} \frac{\partial f}{\partial q^i} \partial_{q^j} = \sum_i \frac{1}{h_i^2} \frac{ \partial f}{\partial q^i} h_i \hat{\mathbf{e}}_i$

(המעבר השלישי נעשה כי $g^{ij}$ מטריצה אלכסונית, $g^{ij} = (1/h_i^2) \delta^{ij}$ כאשר $\delta^{ij}$ היא הדלתא של קרונקר)
ובסך הכל נקבל

$\nabla f= \frac{1}{h_1} \frac{\partial f}{\partial q^1} \hat{\mathbf{e}}_1+ \frac{1}{h_2} \frac{\partial f}{\partial q^2} \hat{\mathbf{e}}_2 + \frac{1}{h_3} \frac{\partial f}{\partial q^3} \hat{\mathbf{e}}_3$

קשרים בין אופרטורים

• דיברגנץ, גרדיאנט ולפלסיאן: $\operatorname{div} \ \operatorname{grad} = \Delta$

משפט הגרדיאנט

משפט הגרדיאנט אומר שאם $f(\mathbf{r}) = f(x,y,z)$ היא שדה סקלרי (פונקציה $f:\mathbb{R}^3 \to \mathbb{R}$ ) חלק מספיק (גזיר ברציפות), אזי לכל מסילה שמתחילה בנקודה כלשהי A ומסתיימת בנקודה כלשהי B האינטגרל הקווי על $\nabla f$ לאורך המסילה לא תלוי במסילה עצמה אלא רק בנקודות הקצה ומתקיים

$\int_\mathbf{A}^\mathbf{B} \nabla f \cdot d\mathbf{r} = f(\mathbf{B})-f(\mathbf{A})$

לשדה הווקטורי $\nabla f$ קוראים "שדה וקטורי משמר" או בהקשר של פיזיקה "כוח משמר" ומתקיים

$\nabla \times \nabla f = 0$

ראו גם

• פונקציונל
• טנזור
• קואורדינטות

לקריאה נוספת

• מורי ר. שפיגל, אנליזה וקטורית, סדרת שאום