קרטוגרפיה


קַרְטוֹגְרַפְיָה (בעברית: מַפָּאוּת) היא תורת היצירה, העריכה, הקריאה, העיבוד וההדפסה של מפות גאוגרפיות. המפה היא תיאור מישורי מוקטן, מכוון, בר מדידה וסכמתי של תופעות גאוגרפיות על פני כדור הארץ.
על פי רוב, מבחינים בין מפות פיזיות אשר עוסקות בפני השטח (הרים, מישורים, ימים, אגמים, נחלים וכדומה), לבין מפות מדיניות, אשר מציינות גבולות בין מדינות על פי קנה מידה מוגדר ומצוין. קיימות גם מפות נושאיות המציינות אקלים, כמות משקעים, גודל אוכלוסייה, התפלגות דתות וכו'.
אטימולוגיה[עריכת קוד מקור | עריכה]
מקור המלה קרטוגרפיה, ובכתיב ארכאי כרטוגרפיה, בשפה היוונית. המילה היוונית "Χάρτης", כָרְטֶס (כ"ף רפה) מציינת גיליון כתוב או מפה, ו"גרפיה" מלשון כתיבה.
תחומי העיסוק של הקרטוגרפיה[עריכת קוד מקור | עריכה]
קרטוגרפיה בעת החדשה עוסקת בהכנה של מפות אשר מיועדות לייצג מידע גאוגרפי מסוגים שונים ולמטרות שונות בצורה נוחה לשימוש. במשך מאות שנים רוב המפות השימושיות היו תרשימים דו-ממדיים שהודפסו לרוב על גבי נייר (אם כי נוצרו גם גלובוסים), ושיטה זו עדיין נמצאת בשימוש נרחב. לעיתים מרוכזות מפות של אזורים שונים או עם מאפיינים שונים בכרכים המכונים אטלס.
 ערך מורחב – מפה
ערך מורחב – מפה
בניית מפה דורשת מגוון של משימות והתמחויות שנכללות בתחום הקרטוגרפיה:
- החלטה על סוג המפה, העצמים המוחשיים או הרעיוניים שייוצגו בה, ורמת הפירוט. לדוגמה, מפה פיזית של מדינה יכולה לכלול מידע מפורט על הרים, עמקים, נהרות, ערים וכבישים; מפה מדינית של יבשת תתמקד בגבולות בין מדינות ובמיקום ערים מרכזיות; מפות אחרות יכולות להתמקד במשאבי טבע ספציפיים, מאפייני אוכלוסייה, ועוד.
- איסוף המידע הדרוש למפה הרצויה ועדכון מידע ישן לפי הצורך. לדוגמה, קואורדינטות של נקודות ציון, גבולות עדכניים של מדינות.
- ייצוג דו-ממדי של המידע המקושר לפני שטח שאינם מישוריים (מפה בודדת יכולה לייצג רק חלק מפני כדור הארץ, ואף זאת לא במדויק). מפות מסוגים שונים משתמשות בהיטלים שונים של פני כדור הארץ על פי הצורך.
- הוספת תוויות וסמלים של שמות או סוגים של פרטי מידע, לדוגמה שמות ערים, סימון ערי בירה.
- הסרה או עריכה של מידע כדי לשפר את קריאות המפה בהתאם למטרתה. לדוגמה, במפות של מדינות בארצות הברית, חלק משמות המדינות הקטנות עשויים להופיע בקיצור או מחוץ לשטח המדינה; איים קטנים המופיעים במפות ניווט ימיות לא בהכרח יופיעו במפות פיזיות.
- עיצוב גרפי שמסייע לקורא בהבנת המידע, לדוגמה צביעת מדינות סמוכות בצבעים שונים במפה מדינית.
בעשורים האחרונים, מפות הנייר מוחלפות על ידי מערכות מידע גאוגרפי אשר מאפשרות הצגת מידע מסוגים שונים לפי בחירה באופן דינמי, ולמעשה בניה אינטראקטיבית של מפה למטרה ספציפית רצויה. בהתאם לכך, עבודת הקרטוגרפיה מתעדכנת לבניה ולעדכון של מערכת המידע הגאוגרפית.
היסטוריה[עריכת קוד מקור | עריכה]




אין הסכמה לגבי השאלה מה היא המפה העתיקה בעולם, בשל העובדה שהגדרת המושג "מפה" איננה חד משמעית וגם משום שכמה מהחפצים שנראים כמפות אולי בכלל אינם מפות. ציור קיר שנראה כמו שרטוט של העיר האנאטולית צ'אטאלהויוק (Çatalhöyük)[1], מתוארך למאה ה-7 לפני הספירה.
ב-Mount Bego שבאלפים נמצאו חריטות בצורות גרפיות של נקודות וקווים, אשר הארכאולוגים מפרשים אותם כשרטוטי חלקות אדמה מעובדות[2] שנעשו באלף הרביעי לפני הספירה. מפה מתקופת התרבות המינואית היא ציור הקיר "בית האדמירל" מ-1600 לפני הספירה, ובו קהילה השוכנת לחופו של ים ומפה חרוטה של העיר השומרית ניפור[3] מתקופת הכשים.
מפות העולם הבבליות מהמאה ה-6 לפני הספירה הן מפות העולם העתיקות ביותר ששרדו[4].
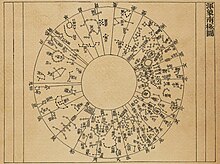
בתולדות סין העתיקה מוכרת ספרות גאוגרפית מהמאה החמישית לפני הספירה. המפות העתיקות ביותר הן ממדינת צ'ין בתקופת המדינות הלוחמות. המדען הסיני סו סונג פרסם בשנת 1092 את מפת הכוכבים המודפסת העתיקה ביותר הידועה בימינו.
בהודו כללו מפות השמים העתיקות את כוכב הצפון וקבוצות כוכבים נוספות שהיו כנראה בשימוש לצורכי ניווט.
מפה מונדי הן מפות עולם אירופאית מימי הביניים. כ-1,100 מפות כאלה שרדו בימינו, ומתוכן כ-900 שימשו לאיור כתבי יד.
הגאוגרף הערבי מוחמד אל-אדריסי הוציא לאור בשנת 1154 אטלס בשם טבולה רוג'ריאנה, "ספר המסעות הנעימים לארצות רחוקות" نزهة المشتاق في اختراق الآفاق, בו נכלל מידע אודות אפריקה, האוקיינוס ההודי והמזרח הרחוק, כפי שנמסר על ידי סוחרים ערביים ומגלי עולם ומידע נוסף שהיה נחלת גאוגרפים בתקופתו. אטלס זה היה מקור המידע הגאוגרפי העולמי המהימן ביותר בתקופתו והחזיק במעמד זה במשך 300 שנה[5].
בעידן התגליות, בין המאות 15 וה-17 קרטוגרפים אירופאים נהגו להעתיק מפות קודמות, כמה מהן בנות מאות שנים. בנוסף לכך הם שירטטו מפות לפי תיאורים ששמעו מפי נוסעים בני זמנם, בהשתמשם בטכניקות הסריקה שהיו נהוגות בתקופה. המצאת המצפן, הטלסקופ והסקסטנט הבטיחו מידה רבה יותר של דיוק. בשנת 1492 יצר הקרטוגרף הגרמני Martin Behaim את הגלובוס הראשון הקיים עד ימינו.
ב-1507 ייצר Martin Waldseemüller מפה מעוגלת של העולם ומפת קיר של העולם (Universalis Cosmographia), בנויה מ-12 לוחות ובה מצוינת לראשונה המילה אמריקה.
בשל הקשיים הרבים הכרוכים בייצור מפות, לעיתים העתיקו הקרטוגרפים מפות ישנות, מבלי לתת קרדיט לצייר המקורי. למשל, אחת המפות העתיקות ביותר של אמריקה הצפונית ידועה בשם "מפת הבונה" ("Beaver Map"), אשר פורסמה ב-1715 בידי הקרטוגרף והמוציא לאור Herman Moll. אבל למעשה זה שעתוק מדויק של מפה משנת 1698 מאת Nicolas de Fer, שהעתיק חלקים שהופיעו לראשונה בספריו של Louis Hennepin משנת 1697 ושל François Du Creux מ-1664. מהמאה ה-18 החלו קרטוגרפים לתת קרדיט למקורותיהם בזו הלשון:"לאחר [שמו של הקרטוגרף המקורי]" ("[After [the original cartographer")[6].
רשת קואורדינטות ארצית[עריכת קוד מקור | עריכה]

רשת קואורדינטות ארצית היא רשת דמיונית ושרירותית של קווים אנכיים ואופקיים, שבעזרתה ניתן לקבוע מיקומו של עצם בשטח המדינה. רשת זו דומה לרשת קווי האורך וקווי הרוחב הגאוגרפיים של כדור הארץ. אף שהרשת העולמית של קווי האורך וקווי הרוחב היא רשת קואורדינטות גאוגרפיות קבועות הנמדדות בדיוק של מעלות, דקות ושניות, בעוד שרשת הקואורדינטות הארצית היא רשת שרירותית ויחסית, אשר אינה מגיעה לדיוק כה גדול, בכל זאת, החיסרון הבולט הבא ברשת קווי האורך וקווי הרוחב העולמית גורם דווקא לרשת הקואורדינטות הארצית להיות מועדפת במצבים מסוימים: רשת קווי האורך וקווי הרוחב העולמית ממפה כדור (וליתר דיוק, אליפסה) לפי חישוב של היקף שאינו מדויק. גם לאחר שמוסיפים חישובים גאומטריים המתחשבים בהיותו של כדור הארץ אליפטי, עדיין פני הים של כדור הארץ הגיאואידי, חורגים מן הנוסחאות, בשל העובדה שפני כדור הארץ אינם משטח אליפטי אחיד, אלא חורגים ממנו, הן כלפי מעלה והן כלפי מטה במספר אזורים.
לכן, נוצר צורך מיוחד ליצור מערכות ייחוס שונות לאזורים גאוגרפיים שונים על פני כדור הארץ, באופן שמתחשב בחריגות של פני כדור הארץ מנוסחת האליפסה. רשתות יחסיות אלו שאותן קובעות רשויות המדידה שבכל מדינה, הן מערכות ייחוס של קואורדינטות קרטזיות "שטוחות", הנמדדות בקילומטרים ומטרים, ומתאימות בדיוק לאזור שנועדו לו. כך למשל, בניווט באמצעות GPS נעשה שימוש במערכת ייחוס הקרויה WGS-84, אשר קרובה בחישוביה למשטח הגיאואידי של פני כדור הארץ.
בעיה נוספת בהצגת פני כדור הארץ על פני מפה שטוחה, בעיה המשותפת לשתי מערכות הקואורדינטות, הן הארצית והן העולמית, היא המרת פני השטח הכדוריים של כדור הארץ לפני שטח של מפה שטוחה. כדי לעשות זאת יש צורך להשתמש בהיטל. ישנם היטלים מסוגים שונים כמו היטל קסיני סולדנר, היטל רובינסון והיטל מרקטור רוחבי. רשת UTM למשל, משתמשת בהיטל גלילי, שהוא היטל מרקטור רוחבי, שבו כדור הארץ מוטל על פנים גליל, המושטח לאחר מכן. לפי Theorema Egregium לא קיים היטל מושלם השומר על כל הגדלים במדויק. [7]
ראו גם[עריכת קוד מקור | עריכה]
- היטל
- דאטום (גאודזיה)
- האגודה הישראלית לכרטוגרפיה ולמערכות מידע גאוגרפי
- מיפוי דיגיטלי
- המיפוי הטריגונומטרי הגדול
- תצלום לוויין
- גאוגרפיה
לקריאה נוספת[עריכת קוד מקור | עריכה]
- נפתלי קדמון ואבשלום שמואלי, מפות ומיפויון, הוצאת כתר, 1982.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- הלל בירגר, המפה ושימושה הצבאי, מערכות גיליון מחנות, נובמבר 1939
- היטלים
- אתר המציג מפות של ערים היסטוריות
- הערך "קורדינאטות ארציות", באתר אסטרופדיה
- ההיסטוריה של הקרטוגרפיה(הקישור אינו פעיל), מצגת באתר אוניברסיטת בר-אילן
- איילת שטיין ואייל מהריאן, מפות ומפוי של מגלי עולם, מצגת באתר הלשכה המרכזית לסטטיסטיקה
- מפות עתיקות, חבילת תוכן באתר החינוך של הספרייה הלאומית
- קרטוגרפיה, סוגי מפות ותצלומי אוויר, באתר לרגו
- קרטוגרפיה, באתר אנציקלופדיה בריטניקה (באנגלית)
 הניו יורק טיימס, חוקרים יצרו מפה דו-צדדית, שמתארת את העולם באופן מדויק, באתר הארץ, 8 במרץ 2021[8]
הניו יורק טיימס, חוקרים יצרו מפה דו-צדדית, שמתארת את העולם באופן מדויק, באתר הארץ, 8 במרץ 2021[8] תהליך מיפוי ארץ ישראל, 1957, באתר ארכיון הסרטים הישראלי בסינמטק ירושלים
תהליך מיפוי ארץ ישראל, 1957, באתר ארכיון הסרטים הישראלי בסינמטק ירושלים- קרטוגרפיה, באתר MathWorld (באנגלית)
 קרטוגרפיה, דף שער בספרייה הלאומית
קרטוגרפיה, דף שער בספרייה הלאומית
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ New Paintings Discovered at Çatalhöyük in 2011 באתר catalhoyuk, excavations of a neolithic anatholian hoyuk, נראה בתאריך 10 בינואר 2015
- ^ Arcà, Andrea (2004). The topographic engravings of the Alpine rock-art: fields, settlements and agricultural landscapes. In Chippindale C., Nash G. (eds.) The figured landscapes of Rock-Art, Cambridge University Press, pp. 318-349; online academia.edu, retrieved December 2, 2014.
- ^ The Nippur Expedition, The University of Chicago
- ^
 צביה לוטן, מיפוי - התפתחות המיפוי באירופה, באתר הספרייה הווירטואלית של מטח
צביה לוטן, מיפוי - התפתחות המיפוי באירופה, באתר הספרייה הווירטואלית של מטח
- ^ הספר של רוג'ר, אתר לימודי של אוניברסיטת חיפה
- ^ ARCHIVED - Detecting the Truth. Fakes, Forgeries and Tricker
- ^ קולו אור, הכדור הוא עגול, במדור "מדע במבט-על" באתר של מכון דוידסון לחינוך מדעי, 29 בספטמבר 2022
- ^ תצוגת המפה באתר אוניברסיטת Princeton
