תחום שלמות

באלגברה מופשטת, תחום שלמות הוא חוג חילופי עם יחידה כפלית שאין בו מחלקי אפס (כלומר: אם $ab=0$, אז בהכרח $a=0$ או $b=0$). בין הדוגמאות החשובות ניתן למצוא כל תת-חוג של הממשיים, ומכאן חשיבותה של המשפחה הזו בתורת המספרים האלגברית.

תחומי שלמות ושדות

כל שדה הוא תחום שלמות, משום שהאברים השונים מאפס כולם הפיכים, ולכן לא ייתכן ש-ab=0 כאשר a,b אינם אפס. מכיוון שהאיסור על קיומם של מחלקי אפס עובר בתורשה לתת-חוגים, כל תת-חוג של שדה הוא תחום שלמות. בין הדוגמאות הטבעיות לתחומי שלמות שאינם שדות אפשר למצוא את חוג המספרים השלמים, ואת חוג הפולינומים עם מקדמים משדה $F$, אותו מסמנים ב- $F[x]$.

בכיוון ההפוך, כל תחום שלמות מהווה תת-חוג של שדה, הנקרא שדה השברים של התחום. שדה השברים כולל את כל המנות ${\frac {a}{b}}$ של איברים בחוג שבהן המכנה אינו אפס. למשל, שדה השברים של $\mathbb {Z}$ הוא שדה המספרים הרציונליים $\mathbb {Q}$, בעוד ששדה השברים של חוג הפולינומים הוא שדה הפונקציות הרציונליות $F(x)=\left\{{\frac {f}{g}}:f,g\in F[x],\,g\neq 0\right\}$. הבניה של שדה השברים מתוך התחום הנתון היא דוגמה למיקום (לוקליזציה).

בתחום שלמות, אוסף האיברים שאינם אפס סגור לכפל, ולכן מהווה מונואיד עם צמצום: אם $ab=ac$ אז $b=c$. כל מונואיד סופי עם צמצום הוא חבורה, ולכן תחום שלמות סופי הוא שדה.

יחס החלוקה בתחומי שלמות

עבור תחום שלמות קבוע $D$, אומרים שאיבר $a$ מחלק את האיבר $b$ אם קיים איבר $c$ כך ש-$b=ac$ (זוהי הכללה של ההגדרה הרגילה במספרים שלמים). כל איבר מחלק את $0$, ו-$1$ מחלק כל איבר. איבר המחלק את $1$ נקרא איבר הפיך (למשל: בחוג השלמים האיברים ההפיכים הם $1,-1$. בשדה, כל האיברים הם הפיכים פרט לאפס). איברים המחלקים זה את זה נקראים ידידים.

איבר של החוג נקרא אי-פריק, אם לא ניתן לכתוב אותו בצורה $ab$ כאשר $a$ ו-$b$ אינם הפיכים. ישנו סוג מיוחד של איברים אי-פריקים, הנקראים ראשוניים. איבר ראשוני הוא איבר שאינו יכול לחלק מכפלה $ab$ בחוג, מבלי לחלק לפחות את אחד הגורמים שלה. ראשוני מוכרח להיות אי-פריק (אם אפשר לפרק את הראשוני $p$ בצורה $p=ab$ אז $p$ מוכרח לחלק את אחד הגורמים, למשל את $a$, ואז יוצא ש-$b$ הפיך), אבל ישנם איברים אי-פריקים שאינם ראשוניים (ראה דוגמאות בהמשך). שתי ההגדרות מכלילות את ההגדרה הרגילה למספרים ראשוניים (לפי הלמה של אוקלידס, בחוג המספרים השלמים איבר הוא ראשוני אם ורק אם הוא אי-פריק, והמספרים בעלי תכונה זו הם המספרים הראשוניים הרגילים).

דוגמה: בתחום-השלמות $R=\mathbb {Z} [{\sqrt {-6}}]=\{a+b{\sqrt {-6}}:a,b\in \mathbb {Z} \}$, האיבר $2-{\sqrt {-6}}$ אי-פריק, אבל אינו ראשוני (הוא מחלק את 10 אבל לא את הגורמים 2 או 5).

מחלקות של תחומי שלמות

סריג מחלקות של תחומי שלמות: דדקינד, פרופר ובזו, תחומים ראשיים, תחומי פריקות יחידה, תחומים אטומיים, תחומים בעלי gcd, ועוד.

התכונות של איברים אי-פריקים וראשוניים באות לידי ביטוי כשבוחנים את תהליך הפירוק לגורמים של איבר נתון $a$. אם $a$ אי-פריק, סיימנו לפרק אותו; אחרת, אפשר לכתוב את $a$ כמכפלה של איברים אחרים, ולהמשיך לפרק כל אחד מהם. בחוגים מסוימים (בעיקר חוגים נותריים) מובטח שהתהליך יעצר, בדיוק כפי שהתהליך של פירוק מספר שלם לגורמיו חייב להעצר. בסופו של פירוק כזה כתבנו את $a$ כמכפלה של איברים אי-פריקים (חוג שבו תמיד קיים פירוק כזה נקרא אטומי). לרוע המזל, (ולא כמו במספרים השלמים), פירוק כזה אינו חייב להיות יחיד. (דוגמה: המספרים $2,3,{\sqrt {-6}}$ בחוג $R$ שהוגדר לעיל הם כולם אי-פריקים, והנה $6=2\cdot 3=-1\cdot {\sqrt {-6}}\cdot {\sqrt {-6}}$, שני פירוקים שונים לאותו מספר).

מתברר שאם הגורמים האי-פריקים בפירוק הם כולם ראשוניים, אז אין פירוקים אחרים (פרט לזה שאפשר להחליף גורם בידיד שלו, ולערבב את הגורמים ביניהם). תחום שלמות שבו כל איבר ניתן לפירוק כמכפלה של אי-פריקים, וזה ניתן להעשות באופן יחיד, נקרא תחום פריקות יחידה. בחוג כזה כל איבר אי-פריק הוא גם ראשוני.

ישנו תנאי המבטיח פריקות יחידה: תחום שלמות $D$ שבו כל אידיאל הוא אידיאל ראשי (כלומר מהצורה $Da=\{xa:x\in D\}$), נקרא תחום ראשי. כל תחום ראשי הוא תחום פריקות יחידה, אבל ההפך אינו נכון (דוגמה: חוג הפולינומים בשני משתנים מעל שדה הוא תחום פריקות יחידה שאינו ראשי). לתחום ראשי יש ממד קרול 1, כלומר, כל אידיאל ראשוני שונה מאפס הוא מקסימלי.

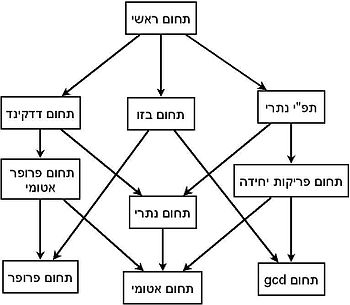
כל חוג אוקלידי הוא תחום ראשי, וכל תחום ראשי הוא חוג דדקינד. כל חוג דדקינד הוא תחום שלמות נותרי וכל תחום שלמות נותרי הוא אטומי. בדיאגרמה משמאל מוצג סריג של מחלקות חשובות של תחומי שלמות: תחומי דדקינד, תחומי פרופר, תחומים ראשיים, תחומי פריקות יחידה, תחומי בזו, תחומים אטומיים, תחומים בעלי gcd, ועוד. השילוב של שתי תכונות הוא התכונה החלשה ביותר שחזקה משתיהן; כך למשל תחום פרופר נתרי הוא תחום דדקינד, תחום בזו אטומי הוא ראשי, וכן הלאה.

תחום שלמות רגולרי נתרי הוא תחום פריקות יחידה (Auslander-Buchsbaum, 1959).

אידיאלים בתחומי שלמות

אידיאלים שבריים

יהי R תחום שלמות, ו-F שדה השברים שלו. אידיאל שברי של R הוא תת-קבוצה של F מהצורה $d^{-1}A$, כאשר $d\in R$ ו-$A$ אידיאל של R. ההגדרה הזו מניחה ש-d הוא מעין "מכנה משותף" של היוצרים, על אף ש-A אינו בהכרח נוצר סופית. אידיאלים שבריים דומים זה לזה אם אחד מהם מתקבל מהשני על ידי כפל בקבוע (של F).

כמו אוסף האידיאלים, אוסף האידיאלים השבריים סגור לכפל, אלא שבניגוד אליו הוא כולל גם איברים הפיכים: אומרים ש-A,B הופכים זה את זה אם $AB=R$ (כלומר, קיימים $a_{1},\dots ,a_{n}\in A$ ו-$b_{1},\dots ,b_{n}\in B$ כך ש-$a_{1}b_{1}+\cdots +a_{n}b_{n}=1$). אידיאל שברי הפיך חייב להיות נוצר סופית. תחום שלמות הוא תחום דדקינד אם ורק אם כל האידיאלים השבריים הפיכים, ותחום פרופר אם ורק אם כל האידיאלים השבריים הנוצרים סופית הם הפיכים.

אוסף האידיאלים השבריים ההפיכים מהווה חבורה, שמסמנים $\operatorname {Inv} (R)$. כל אידיאל שברי ראשי הוא הפיך. זה מגדיר סדרה קצרה מדויקת $0\rightarrow F^{\times }/R^{\times }\rightarrow \operatorname {Inv} (R)\rightarrow \operatorname {Pic} (R)\rightarrow 0$, המגדירה את חבורת פיקארד של החוג. אם R תחום דדקינד, החבורה הזו היא חבורת המחלקות.

פעולת ההיפוך

עבור אידיאל שברי $I$, מסמנים $I'=\{x\in F:xI\subseteq R\}$ (מקובלים גם הסימונים $R:I$ ו-$I^{-1}$). זו פעולה הופכת סדר המקיימת $I\subseteq I''$ (ולכן זו התאמת גלואה מופשטת). בפרט מתקיים תמיד $I'''=I'$. הפעולה מכבדת דמיון ($(\alpha I)'=\alpha ^{-1}I'$ לכל $\alpha \in F$).

לפי ההגדרה $II'\subseteq R$, ו-$I'$ הוא האידיאל השברי המקסימלי המקיים תנאי זה. אם $I$ הפיך, אז ההפכי שלו שווה ל-$I'$.

סגור-v

החסרון העיקרי של החבורה $\operatorname {Inv} (R)$ הוא בכך שהיא "רואה" רק אידיאלים נוצרים סופית. כדי לצרף אידיאלים שאינם נוצרים סופית למשחק הזה, יש להכליל את מושג ההפיכות.

הפעולה $I\mapsto I''$ היא אידמפוטנטית, שומרת סדר, ומקיימת $I\subseteq I''$. הפעולה נקראת בדרך כלל סגור-v, עם הסימון $I^{v}=I''$. אידיאל המקיים $I=I''$ (כלומר אידיאל סגור-v) הוא אידיאל דיביזורי (divisorial). אידיאל הוא דיביזורי אם ורק אם הוא מהצורה $I'$. תחום שלמות שבו כל האידיאלים דיביזוריים נקרא תחום דיביזורי. בפרט כל תחום דדקינד הוא דיביזורי, ובפרט גם כל תחום הערכה דיסקרטי. זה אינו תנאי טריוויאלי: האידיאל המקסימלי בתחום הערכה שאינו דיסקרטי אינו דיביזורי.

אפשר לתאר את סגור-v כחיתוך $I^{v}=\bigcap _{I\subseteq Rx}Rx$ האידיאלים השבריים הראשיים המכילים את I. יש תיאור מועיל נוסף, במונחים של תחומי הערכה, המבוסס על כך שהמשפחה של תחומי ההערכה המכילים את R (בתוך F) היא עדינה מספיק בכדי להפריד אידיאלים: אם $I\not \subseteq J$ אז קיים תחום הערכה $R\subseteq V\subseteq F$ כך ש-$VI\not \subseteq RJ$ (זו תוצאה של הלמה של צורן). מעובדה זו נובע התיאור של סגור-v כחיתוך $I''=\bigcap _{V}(VI)$ (החיתוך על תחומי ההערכה כדלעיל).

מן השוויון $(I^{v}J)^{v}=(IJ)^{v}$ נובע שמכפלת-v המוגדרת לפי $I*J=(IJ)^{v}$ היא אסוציאטיבית. מכפלת-v מתלכדת עם המכפלה הרגילה אם $I$ או $J$ הפיכים. בפרט, אוסף האידיאלים הדיביזוריים מהווה מונויד ביחס למכפלת-v. אם $I$ הפיך-v, אז ההפכי הדיביזורי (היחיד) שלו הוא $I'$. לכן $\operatorname {Div} (R)=\{I:\,I''=I,\,I*I'=R\}$ היא חבורה, המכילה את $\operatorname {Inv} (R)$ כתת-חבורה.

תחום שלמות שבו כל אידיאל דיביזורי הוא הפיך ביחס למכפלת-v, נקרא תחום סגור בשלמות לחלוטין (completely integrall closed, ובקיצור CIC). כל תחום קרול, ובפרט כל תחום דדקינד, הוא CIC. בתחום CIC המנה $\operatorname {Div} (R)/(F^{\times }/R^{\times })$ נקראת חבורת המחלקות. חבורת המחלקות מכילה את חבורת פיקארד כתת-חבורה.

סגור-t

סגור-t הוא עידון של סגור-v, המוגדר לפי $I^{t}=\bigcup J^{v}$ כאשר האיחוד על האידיאלים השבריים הנוצרים סופית $J\subseteq I$. כך מתקיים תמיד $I\subseteq I^{t}\subseteq I^{v}$, עם שוויון $I^{t}=I^{v}$ כאשר I נוצר סופית (וממילא בתחום נתרי שתי פעולות הסגור מתלכדות; הפעולות מתלכדות אם ורק אם R הוא תחום מורי, כלומר מתקיים תנאי השרשרת העולה על אידיאלים דיביזוריים). האידיאל הוא t-סגור אם $I^{t}=I$. לפי ההכלה לעיל, כל אידיאל דיביזורי הוא t-סגור (והמושגים מתלכדים על אידיאלים נוצרים סופית).

בדומה למקרה של אידיאלים דיביזוריים, אפשר להגדיר מכפלת-t לפי $I*_{t}J=(IJ)^{t}$. בפרט, אוסף האידיאלים ה-t-סגורים מהווה מונויד ביחס למכפלת-t. כמקודם $\operatorname {Div} _{t}(R)=\{I:\,I^{t}=I,\,I*_{t}I'=R\}$ היא חבורה, עם שיכונים טבעיים $\operatorname {Inv} (R)\leq \operatorname {Div} _{t}(R)\leq \operatorname {Div} (R)$.

מספר היוצרים

בתחום דדקינד כל אידיאל נוצר על ידי שני איברים. כהכללה של עובדה זו, הוכיח Heitmann (1976) שבכל תחום שלמות מממד קרול n, כל אידיאל הפיך נוצר על ידי n+1 איברים (שאת הראשון מביניהם אפשר לבחור כרצוננו).

מודולים מעל תחומי שלמות

קשרים בין אידיאלים, אידיאלים שבריים ומודולים מעל תחום שלמות

חוג חילופי הוא ראשוני אם ורק אם הוא תחום שלמות. תחום שלמות פשוט הוא שדה. תחום שלמות שאינו שדה לא יכול להיות חוג ארטיני.

מעל תחום ראשי, כל מודול נוצר סופית הוא סכום ישר של מודולים ציקליים. זוהי הכללה של משפט המיון לחבורות אבליות נוצרות סופית, ושל הפירוק של מטריצות לבלוקי ז'ורדן.

בדיאגרמה משמאל מוצגות כמה משפחות עיקריות של מודולים מעל תחום שלמות $R$: אידיאלים של $R$, אידיאלים שבריים, ומודולים כלליים: חופשיים, פרויקטיביים, שטוחים וחסרי פיתול. החצים השחורים מסמנים גרירה לוגית של תכונה אחת לאחרת. החצים הצבעוניים מאפיינים מחלקה של תחומי שלמות: תחום שלמות מקיים את אחד החצים הכחולים אם ורק אם הוא דדקינד, ואז הוא מקיים את כולם; וכן לתחומי פרופר, בזו ולתחומי שלמות נתריים.

מודולים ופיתול

איבר (שונה מאפס) $x$ במודול מעל תחום שלמות $R$ הוא מפותל אם קיים סקלר שונה מאפס $a$ כך ש-$ax=0$. המודול מפותל אם כל אבריו מפותלים, וחסר פיתול אם אף איבר שלו אינו מפותל. המודול $A$ מפותל אם ורק אם $F\otimes _{R}A=0$ כאשר $F$ הוא שדה השברים של $R$. כל מודול מהצורה $F\otimes _{R}A$ הוא חסר פיתול, משום שזהו מרחב וקטורי.

מודול הוא חסר פיתול אם פעולת הכפל בכל סקלר שונה מאפס היא חד-חד-ערכית; וחליק אם פעולת הכפל בכל סקלר שונה מאפס היא על. מודול מעל תחום שלמות R נקרא h-חליק אם הוא מנה של מודול אינג'קטיבי. כל מודול h-חליק הוא חליק. מודול חליק וחסר פיתול הוא אינג'קטיבי, ולכן h-חליק. כל מודול מהצורה $\operatorname {Hom} _{R}(F,A)$ הוא h-חליק. המודול R עצמו חסר פיתול, ואינו חליק (אנו מניחים ש-$R\neq F$). כמודול, F הוא חליק וחסר פיתול, וממילא גם אינג'קטיבי. מודול המנה $F/R$ הוא מפותל ו-h-חליק, אבל בדרך כלל אינו אינג'קטיבי (אם $R$ תחום דדקינד אז כל מודול חליק הוא אינג'קטיבי).

מודול נקרא מצומצם (reduced) אם אין לו תת-מודולים חליקים (פרט ל-0), ו-h-מצומצם אם אין לו תת-מודולים h-חליקים. כל מודול מצומצם הוא h-מצומצם. גם כאן, המושגים מתלכדים עבור מודולים חסרי פיתול.

עבור כל מודול $A$, התמונה של ההומומורפיזם הטבעי $\operatorname {Hom} (F,A)\rightarrow A$ (השולח את $f$ ל-$f(1)$) היא תת-המודול ה-h-חליק המקסימלי של $A$. בפרט, $A$ הוא h-מצומצם אם ורק אם $\operatorname {Hom} (F,A)=0$.

הפונקטור Ext ממיין הרחבות של מודולים. בפרט, $\operatorname {Ext} _{R}^{1}(C,A)=0$ אם ורק אם כל סדרה מדויקת קצרה ${\displaystyle 0\rightarrow A\rightarrow$ ?\rightarrow C\rightarrow 0} , מתפצלת. המודול A אינג'קטיבי אם ורק אם $\operatorname {Ext} _{R}^{1}(-,A)=0$. מודול $A$ הוא קו-מפותל (cotorsion) אם $\operatorname {Hom} (F,A)=\operatorname {Ext} _{R}^{1}(F,A)=0$. במקרה כזה $A=\operatorname {Ext} _{R}^{1}(F/R,A)$. כל מודול קו-מפותל הוא h-מצומצם. לכל מודול h-מצומצם $A$, $\operatorname {Ext} _{R}^{1}(F/R,A)$ הוא המודול הקו-מפותל הקטן ביותר המכיל את $A$.

הדואליות בין המושגים הללו באה לידי ביטוי במשפט הבא. עבור R-מודול $A$, נסמן $A^{*}=\operatorname {Hom} (F/R,A)$ (המודול $A^{*}$ תמיד קו-מפותל; אם $A$ חסר פיתול, או h-מצומצם, אז $A^{*}=0$). נסמן ${\widehat {A}}=(F/R)\otimes _{R}A$ (המודול ${\widehat {A}}$ תמיד מפותל; אם $A$ מפותל, או חליק, אז ${\widehat {A}}=0$). כעת:

• $A$ הוא h-חליק ומפותל אם ורק אם $A\cong {\widehat {A^{*}}}$.
• $A$ חסר פיתול וקו-מפותל אם ורק אם $A\cong {\widehat {A}}^{*}$.
• בפרט, אם $A$ הוא h-חליק ומפותל, אז $A^{*}$ חסר פיתול וקו-מפותל; ואם A חסר פיתול וקו-מפותל, אז ${\widehat {A}}$ הוא h-חליק ומפותל; והעתקות אלה הפוכות זו לזו. לדוגמה, מעל השלמים, $\mathbb {Q} _{p}/\mathbb {Z} _{p}$ חליקה ומפותלת, ו-$\mathbb {Z} _{p}$ חסרת פיתול וקו-מפותלת, והן מתאימות זו לזו.

יש מודולים מפותלים שהם קו-מפותלים. מודול $A$ הוא קו-מפותל בחזקה אם $\operatorname {Ext} _{R}^{n}(F,A)=0$ לכל $n\geq 0$. מודול קו-מפותל בחזקה הוא קו-מפותל. אם קיים סקלר $a$ שונה מאפס כך ש-$aA=0$, אז $A$ מפותל, וקו-מפותל בחזקה.

הכללות

חוג שאין בו מחלקי אפס, אבל הוא אינו בהכרח חילופי, נקרא תחום. הדוגמה הטיפוסית כאן היא תת-חוגים של חוגים עם חילוק, אבל יש דוגמאות לתחומים שאינם משוכנים באף חוג עם חילוק (הראשונה ניתנה על ידי Mal'cev ). בתחום אין אידיאלים שמאליים מינימליים, ולכן תחום ארטיני מוכרח להיות חוג עם חילוק. חוג בעל התכונה החלשה יותר "$a^{2}\neq 0$ לכל $a\neq 0$" נקרא חוג מצומצם; כל חוג מצומצם הוא מכפלה ישרה של תחומים, וכל חוג ראשוני מצומצם הוא תחום.

לקריאה נוספת

• Eben Matlis, Torsion-free modules, Chicago Lectures in Math, 1972.

קישורים חיצוניים

• תחום שלמות, באתר MathWorld (באנגלית)