פרופיל אווירודינמי

דוגמאות לפרופילים אווירודינמיים שונים

באווירודינמיקה, פרופיל אווירודינמי הוא צורת החתך של הכנף (של פרופלור, רוטור או טורבינה). גם למפרשים מייחסים פרופיל אווירודינמי. צורת הפרופיל האווירודינמי היא אחד הפרמטרים החשובים המשפיעים על ביצועים של מטוס כמו יצירת כוח העילוי וכוח הגרר כתוצאה מזרימת אוויר על הפרופיל. גוף בעל פרופיל אווירודינמי אשר נע בזורם מייצר כוח אווירודינמי (ראו הסבר מטה). כוח זה נגרם עקב תנועה יחסית בין הגוף והזורם. באופן כללי ניתן לחלק את התרומות לכוח זה לתרומה מלחץ על שפת הגוף (כוח עילוי) בכיוון הניצב אליה ותרומת גזירה עקב צמיגות (כוח גרר).

פרופילים אווירודינמיים של כלים תת-קוליים בדרך כלל מתאפיינים בשפת התקפה עגולה, שפת זרימה חדה ואסימטריה בין המשטח העליון והמשטח התחתון. פרופיל בעל תפקוד דומה בו מים הם הזורם נקרא סנפירית.

העילוי על גבי הפרופיל הוא תוצאה ישירה של זווית ההתקפה שלו וצורתו הגאומטרית. כאשר הפרופיל מוטה בזווית מסוימת, ומשפיע על הזרימה המגיעה אליו, פועל כוח ההפוך בכיוונו לכיוון ההסטה של הזורם. כוח זה נקרא כוח אווירודינמי. רוב הפרופילים זקוקים לזווית הטיה כלשהי כדי לייצר עילוי, אך פרופילים אי-סימטריים יכולים לעשות זאת גם ללא זווית התקפה. ההסטה של הזורם בקרבת הפרופיל גורמת לקווי זרימה מוטים. כתוצאה מכך מקבלים הפרש לחצים בין שני צידי הפרופיל (ואם מדובר בזרימה לא דחיסה ולא צמיגה, ניתן לחשב גם את הפרשי מהירויות על פי משוואת ברנולי). על ידי שימוש בעקרון הסירקולציה, תאוריית קוטה ז'וקובסקי, מקדם עילוי נתון והפרשי המהירויות בין הצד העליון והתחתון של הפרופיל, ניתן לחשב את כוח העילוי.

מבוא

הכנפיים, המייצבים האופקיים והאנכיים של כלי טיס פנויים עם חתכים של פרופילים אווירודינמיים. פרופילים אווירודינמיים נמצאים בשימוש גם בפרופלורים של מסוק, במאווררים ובטורבינות. מפרשים הם פרופילים אווירודינמיים, וגם למשטחים התת-ימיים של סירות כמו השדרית תפקוד דומה. בעלי חיים רבים ואפילו צמחים מסוימים משתמשים באופן טבעי בעקרונות הפרופילים האווירודינמיים. דוגמאות הן ציפורים, דגים וקיפודי ים. פרופיל אווירודינמי יכול לייצר כוח עילוי על כלי רכב ולעזור להנעתו.

קווי זרימה סביב פרופיל NACA 0012 בזווית התקפה בינונית

כל גוף בעל זווית התקפה הנתון לזרימה, כגון פלטה, בניין או גשר, ייצרו את הכוח האווירודינמי עילוי, בכיוון ניצב לזרימה. בתכנון פרופילים אווירודינמיים בדרך כלל המטרה היא להגדיל את העילוי כמה שאפשר מחד גיסא ומאידך גיסא להקטין את הגרר.

עקומת מקדם עילוי לפי זווית ההתקפה של המטוס בהינתן פרופיל אווירודינמי קבוע

משמאל ניתן לראות שני גרפים המתארים את השתנות מקדם העילוי בניסוי מנהרת רוח. הגרף העליון מייצג פרופיל בעל סימטריות ולכן עבורו עילוי אינו מיוצר בזווית התקפה אפס, לעומת פרופיל א-סימטרי שיכול לייצר עילוי בזווית התקפה אפס.

בגרף התחתון ניתן לראות שעם עליית זווית ההתקפה מקדם העילוי עולה ליניארית בקירוב (בשיפוע כמעט קבוע), אך בסביבות 18 מעלות ישנה הזדקרות ומקדם העילוי נופל במהירות. נפילת מקדם העילוי מתרחשת בגלל התנתקות שכבת הגבול במשטח העליון. אפקטיבית, שינוי עובי שכבת הגבול משנה את צורת הפרופיל ומוריד את האפקטיביות של אי הסימטריות של הפרופיל על ידי הורדת הסירקולציה סביבו ובעקבות כך גם את העילוי. גדילת עובי שכבת הגבול גורמת גם להוספת גרר.

עיצוב של הפרופיל האווירודינמי הוא שיקול משמעותי בתחום האווירודינמיקה. ישנם סוגי פרופילים שונים לתחומי תעופה שונים. לדוגמה, פרופילים סימטריים לא מייצרים עילוי בזווית התקפה אפס ולכן הם טובים יותר לטיסה הפוכה האופיינית למטוסי אווירובטיקה. פרופיל סימטרי של מאזנים וכנפי קצה תורם להגדלת תחום זוויות ההתקפה המותר ללא הזדקרות. בכך, זוויות התקפה רבות יכולות לבוא לידי שימוש ללא הפרדת שכבת הגבול במשטח העליון.

פרופילים של כלי טיס על-קוליים מתאפיינים בשפת התקפה חדה, ובאופן כללי מעוגלות יותר מאשר פרופילים של כלי טיס תת-קוליים. שפת ההתקפה החדה גורמת לרגישות גבוהה לזוויות התקפה. על ידי הגדלת העובי של הפרופיל באזור שפת ההתקפה ניתן לגרום לזרימה על-קולית לעבור לתחום התת-קולי. לפרופילים המשמשים לטיסות על קוליות יש בדרך כלל עקמומיות נמוכה על מנת לאפשר טיסה מהירה יותר ללא עלייה משמעותית בגרר. בכנפי כלי טיס מודרניים, ניתן להבחין בשינוי בפרופיל האווירודינמי לאורך הכנף, וזאת כדי להתאים לכל אזור בכנף את הפרופיל המתאים לזרימה האופיינית בו.

לרוב כלי הטיס מותקנים מדפים על הכנפיים. מדף בשפת הזרימה של הפרופיל יכול לשמש במאזן, אך בניגוד למאזן, המדף יכול חלקית להיכנס לכנף כאשר הוא לא בשימוש.

לכנף המיועדת לזרימה למינרית יש עובי מקסימלי בקו הקימור המקסימלי באמצע הכנף. ניתן בעזרת משוואות נאוויה-סטוקס להראות שבתחום הליניארי מפל הלחצים השלילי לאורך הזרימה שקול להורדת המהירות. לכן, עם העקמומיות המקסימלית באמצע, שמירה על זרימה למינרית בחלק גדול יותר מהכנף נהיה אפשרי עבור מהירויות שיוט גבוהות יותר. אולם, בנוכחות גורמים חיצוניים כמו גשם או הפרעות אחרות על גבי הכנף, כבר לא ניתן להשתמש במסקנה זו כיוון שהזרימה הלמינרית כבר לא נשמרת, אלא הופכת לטורבולנטית.

מינוחים

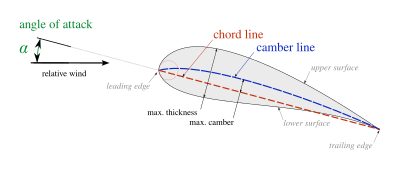
להלן מספר מונחים הקשורים לפרופילים אווירודינמיים:

• משטח עליון (Upper Surface): בדרך כלל נתון למהירות גדולה יותר ולחץ נמוך יותר.
• משטח תחתון (Lower Surface): בדרך כלל נתון למהירות קטנה יותר ולחץ גדול יותר. הפרש הלחצים בין המשטחים תורם לעילוי.
• שפת התקפה (leading edge ): הנקודה בחלק הקדמי של הפרופיל בה העקמומיות מקסימלית.
• שפת הזרימה (Trailing Edge ): הנקודה בחלק האחורי של הפרופיל בה העקמומיות מקסימלית (גדולה בהשוואה בשפת ההתקפה). בנקודה זו לרוב מתנתקת הזרימה.
• מיתר אווירודינמי (Chord Line ): קו ישר המחבר בין שפת ההתקפה לשפת הזרימה. אורך המיתר מסומן בדרך כלל c. אורך המיתר הוא האורך האופייני של הפרופיל.
• קו העקימון (Camber Line ): קו משפת ההתקפה לשפת הזרימה הנמצא במרחק שווה משני משטחי הפרופיל. צורתו תלויה בהתפלגות העובי לאורך המיתר.
• קו אפס-עילוי (Zero-Lift axis ): אם כנף נעה במקביל אל הקו הזה, לא פועל עליה כח עילוי. עבור פרופיל סימטרי קו זה מתלכד עם המיתר האווירודינמי.
• עובי הפרופיל (Boundary layer thickness ): משתנה לאורך המיתר. ניתן להעריך עובי על סמך שתי דרכים:
  • בניצב למיתר, לפי "המוסכמה הבריטית".
  • בניצב לקו העקימון, לפי "המוסכמה האמריקאית".

• מומנט נטייה (Pitching Moment ): מומנט על פרופיל הכנף הנוצר על ידי הכוח האווירודינמי ביחס למרכז האווירודינמי (ראו הסבר מטה) על פרופיל הכנף.

בנוסף, פרמטרים חשובים לתיאור התנהגות הפרופיל בתנועה בזורם הם:

• המרכז האווירודינמי (Aerodynamic center ): המרחק לאורך המיתר משפת ההתקפה, בו המומנט איננו תלוי במקדם העילוי או בזווית ההתקפה. בנקודה זו מתקיים ${\frac {\partial (C_{M})}{\partial (C_{L})}}=0$, כלומר הנגזרת של מקדם המומנט $C_{M}$ ביחס למקדם העילוי $C_{L}$ בנקודה זו שווה לאפס.
• מרכז הלחץ (Center of pressure ): הנקודה בה פועל שקול כוחות הלחץ (העילוי). חישוב המומנט השקול עקב הלחץ בנקודה זו הוא אפס (המרחק לאורך המיתר משפת ההתקפה, בו המומנט מתאפס).

פרופילי NACA

פרופילי NACA הם פרופילים אווירודינמיים אשר פותחו על ידי הוועדה הלאומית המייעצת לאווירונאוטיקה של ארצות הברית. NACA הגדירה מספר משוואות המייצרות פרופילי כנף לפי הגדרה של 4 ספרות המתארות את צורת הפרופיל:

####NACA

• ספרה #1: הקימור המקסימלי באחוזים מאורך המיתר.
• ספרה #2: המרחק של הקימור המקסימלי בעשרות אחוזים (מאורך המיתר) משפת ההתקפה.
• ספרות #3,4: עובי הפרופיל המקסימלי באחוזים מאורך המיתר.

בעזרת ארבעת הספרות של פרופילי NACA ניתן להגדיר את הצורה הגאומטרית של הפרופיל המדובר ולהסיק על תכונותיו האווירודינמיות.

לדוגמה: פרופיל NACA0012 -

• הספרות 00 מעידות כי זהו פרופיל סימטרי
• הספרות 12 מעידות כי עובי הפרופיל הוא 12% מאורך המיתר.

כיום קיימות תוכניות המיועדות לתכנון פרופילי כנף לפי דרישות, כגון PROFOIL, XFOIL, AeroFOIL.

תורת הכנף הדקה

תורת הכנף הדקה פותחה על ידי המתמטיקאי הגרמני-אנגלי מקס מונק ונערכה על ידי האווירודינמאי הבריטי הרמן גלאורט ועוד רבים אחרים, בשנות ה-20 של המאה ה-20. זוהי תאוריה המקשרת בין זווית ההתקפה לעילוי לזרימות בלתי דחיסות ובלתי צמיגות. התאוריה עושה קירוב של הזרימה סביב פרופיל דק לזרימה דו־ממדית.

בזמן הוצאת התאוריה היא זכתה ליחס רב מהסיבה שסיפקה בסיס לתכונות חשובות של פרופילים בזרימה דו־ממדית:

1. בפרופיל סימטרי, המרכז האווירודינמי ומרכז הלחץ נמצאים במרחק רבע מיתר משפת ההתקפה.
2. בפרופיל עקמומי, המרכז האווירודינמי שוכן במרחק רבע מיתר משפת ההתקפה.
3. השיפוע של גרף מקדם העילוי אל מול זווית ההתקפה הוא $2\pi \!$ לרדיאן. הדבר נכון כאשר זווית ההתקפה מוגדרת ביחס למיתר.

תאוריית הכנף הדקה אינה לוקחת בחשבון את תופעת ההזדקרות.

כתוצאה מ-3 ניתן לקבל כי מקדם העילוי עבור פרופיל עקמומי בעל מוטת כנפיים אינסופית הוא:

$\ C_{L}=C_{L_{0}}+2\pi \alpha$

כאשר $\alpha \!$ היא זווית ההתקפה ברדיאנים ו-$C_{L_{0}}$ הוא מקדם העילוי כאשר $\alpha \!$ אפס. $C_{L_{0}}$ מתאפס עבור פרופיל סימטרי.

פיתוח תורת הכנף הדקה

נבחן פרופיל כנף דקה. על פי משפט קוטה-ז'וקובסקי:

$L^{\prime }=-\rho _{\infty }V_{\infty }\Gamma ,\,$

כלומר, העילוי ליחידת אורך שווה למכפלת הצפיפויות של הזורם, מהירות הזרימה והסירקולציה, המוגדרת ע"י:

$\Gamma =\oint _{C}V\cdot d\mathbf {s} =\oint _{C}V\cos \theta \;ds\,=\int _{C}\gamma (x)d{x}$

לכן, על מנת להגיע לעילוי, עלינו לדעת את פילוג הערבוליות על פני הפרופיל. נניח כי תנאי השפה של אי חדירה מתקיים לא רק על שפת הכנף אלא גם על המיתר שלה. הנחה זו סבירה אם הפרופיל "דק מספיק" ומסתכלים עליו "מרחוק מספיק". נסמן ב-$w$ את רכיב המהירות הניצב לקו המיתר. משמעות ההנחה היא ש-$w$ על גבי המשטח העליון של הפרופיל ועל גבי המיתר שווים (מתאחדים).

נדרוש: $U_{n}+w(s)=0$, כאשר $U_{n}$ הוא רכיב המהירות המציפה $U$ שמכתיבה הזרימה שמסביב לפרופיל, בכיוון ניצב למיתר, ו-$s$ הוא פרמטר אורך שמתקדם על המשטח העליון (קו העקימון $y_{c}(x)$, $x$ הוא פרמטר אורך שמתקדם על המיתר).

ממשואות פוטנציאליות של מקור (ראו: זרימה פוטנציאלית), מידת ההשפעה על $w(x)$ של קטע $d\zeta$ על נקודה $x$:

$dw=-{\frac {\gamma (\zeta )d\zeta }{(x-\zeta )2\pi }}$

ולכן באמצעות אינטגרציה נוכל למצוא את השפעת כל המקורות יחד על מיתר:

$w(x)=-\int _{0}^{c}{\frac {\gamma (\zeta )}{(x-\zeta )2\pi }}d\zeta$

נציב את הנ"ל בדרישה שרשמנו ונקבל:

$U(\alpha -{\frac {dy_{c}(x)}{dx}})={\frac {1}{2\pi }}\int _{0}^{c}{{\frac {\gamma (\zeta )}{(x-\zeta )}}d\zeta }$

הבעיה עכשיו היא לפתור את המשוואה האינטגרלית שהתקבלה. לשם כך, נבצע החלפת משתנים:

$\zeta ={\frac {c}{2}}(1-cos(\phi ))$, $x={\frac {c}{2}}(1-cos(\theta ))$

כאשר $\phi$ הוא פרמטר משתנה ו-$\theta$ הוא קבוע עבור על משוואה אינטגרלית נפרדת. הוא קבוע מכיוון שבכל משוואה, $x$ הוא קבוע. כלומר, המשוואה היא על משתנה דמה $\zeta$ שאיתו מגיעים ל-$\gamma (x)$ עבור $x$ מסוים. לאחר הצבת החלפת המשתנים נקבל:

${\frac {1}{2\pi }}\int _{\phi =0}^{\pi }{\frac {\gamma (\theta )sin(\theta )d\theta }{cos(\phi )-cos(\theta )}}=U(\alpha -{\frac {dy_{c}(x)}{dx}})$

ומתנאי קוטה: $\gamma (\phi =\pi )=0$.

על ידי שימוש בפתרון טורי פורייה ניתן לקבל:

$\gamma (\theta )=2U(A_{0}cot(\phi /2)+\sum _{n=1}^{\infty }A_{n}\;\sin(n\phi ))$

כאשר מקדמי פורייה שמתקבלים הם:

$A_{0}=\alpha -{\frac {1}{\pi }}\int _{\phi =0}^{\pi }{\frac {dy_{c}}{dx}}d\phi$, $A_{n}={\frac {2}{\pi }}\int _{\phi =0}^{\pi }{\frac {dy_{c}}{dx}}cos(n\phi )d\phi$.

לפי משפט קוטה-ז'וקובסקי, כוח העילוי $L^{\prime }$ ניתן לחישוב על ידי:

$L^{\prime }=\rho _{\infty }U\int _{0}^{c}{\gamma (x)dx}$

המומנט ביחס לשפת ההתקפה יתקבל על ידי:

$M=\rho _{\infty }U\int _{0}^{c}{x\gamma (x)dx}$

מקדם העילוי יהיה תלוי רק בשני המקדמים הראשונים בטור:

$C_{L}=2\pi (A_{0}+A_{1}/2)$

ומקדמי המומנט סביב שפת ההתקפה ורבע מיתר הם:

$\ C_{M}=-0.5\pi (A_{0}+A_{1}-A_{2}/2)$

$\ C_{M}(1/4c)=-\pi /4(A_{1}-A_{2})$

זווית התקפה

ערך מורחב – זווית התקפה

זווית התקפה חיובית

זווית התקפה זוהי הזווית בין כיוון הזרימה החופשית של האוויר (זרימה כנגד הפרופיל) לבין מיתר הפרופיל. לזווית ההתקפה חשיבות רבה מאוד, וכל שינוי בזווית ההתקפה משפיע על התכונות האווירודינמיות של פרופיל הכנף.

כאשר קו זרימת האוויר מקביל למיתר, זווית ההתקפה תהיה - 0. כאשר שפת ההתקפה תעלה מעל קו זווית - 0, זווית התקפה תהיה חיובית. כאשר שפת התקפה תרד מתחת לקו - 0, זווית התקפה תהיה שלילית.

עבור כל סוג פרופיל קיימת זווית התקפה מינימלית שבה נוצר כוח עילוי שהיא בין הערכים הנמוכים של זווית חיובית (סביבות 1-2 מעלות) ועד ערכים של זווית שלילית קטנות (סביבות מינוס 1-2 מעלות). קיימת גם זווית התקפה שעבורה העילוי הוא מרבי (סביב 18 מעלות). הגדלת זווית ההתקפה מעבר לזווית של עילוי מרבי תגרום להקטנה של כוח עילוי עד להזדקרות (נתק של זרימה אוויר מהפרופיל) ואיבוד העילוי.

קישורים חיצוניים

• פרופיל אווירודינמי, באתר אנציקלופדיה בריטניקה (באנגלית)
• סנפירים, דף שער בספרייה הלאומית