חור שחור אקוסטי
חור שחור אקוסטי (או חור שחור קולי) הוא תופעה שבה גלי קול אינם מסוגלים לברוח מזורם שנע מהר יותר ממהירות הקול המקומית. החור השחור האקוסטי מכונה כך מכיוון שהוא כולא פונונים (קוונטות של גלי קול) באופן דומה לכליאה של פוטונים (קוונטות של גלי אור) על ידי חור שחור אסטרונומי (כבידתי), הידוע בכך שאור שעובר במרחק מספיק קרוב אליו אינו מסוגל לברוח ממנו.
לחור השחור האקוסטי יש נקודות דמיון רבות לחור השחור האסטרונומי, ובפרט הצפי התאורטי לכך שיפלוט את הגרסה הפונונית (קולית) של קרינת הוקינג. קרינה זו היא תופעה קוונטית, וצופים שהיא תיפלט מהגבול של החור השחור האקוסטי (אשר מכונה אופק האירועים האקוסטי), בו מהירות הזרימה משתנה ממהירות הקטנה ממהירות הקול למהירות הגדולה ממהירות הקול.
ישנן מערכות שונות שיכולות לשמש ליצירת חורים שחורים אקוסטיים, והעובדה שמערכות רבות כל כך מחקות כבידה מהווה מעין ראיה לתאוריה של כבידה מתהווה ספונטנית שיכולה לעזור לחבר את תורת היחסות עם מכניקת הקוונטים, בעיה עמוקה בפיזיקה שעדיין לא נפתרה.[1]
ב-2019, לראשונה נמצא אישוש לקרינת הוקינג על ידי יצירת חור שחור קולי. את המדידה ביצע החוקר הישראלי פרופ' ג'ף סטיינהאור מהטכניון על ידי כך שיצר מודל במעבדה המדמה את הקרינה הנפלטת מחור שחור[2]
היסטוריה[עריכת קוד מקור | עריכה]
קרינת הוקינג[עריכת קוד מקור | עריכה]

 ערך מורחב – קרינת הוקינג
ערך מורחב – קרינת הוקינג
הפיזיקאי סטיבן הוקינג הגה ב-1975 את הרעיון שחורים שחורים הם לא לחלוטין "שחורים", אלא פולטים קרינה אלקטרומגנטית לכל הכיוונים - קרינה המכונה קרינת הוקינג. קרינה זו ניתנת להסקה מהחלת כלים מתורת השדות הקוונטית על אופק האירועים של החור השחור היחסותי. בגלל אופייה של הקרינה, שהיא חלשה יותר ככל שמסת החור השחור גדולה יותר, והמרחקים העצומים בין כדור הארץ לחורים שחורים אסטרונומיים בחלל, קרינה זו חלשה מאוד בהגיעה לכדור הארץ ולכן טרם נמדדה באופן ניסויי.
אנלוגיית כבידה[עריכת קוד מקור | עריכה]

הרעיון של חור שחור אקוסטי הוצע לראשונה בשנת 1981 על ידי הפיזיקאי ויליאם אונרו, שפיתח שיטה למיפוי של אספקטים שונים של פיזיקת חורים שחורים לפיזיקה של זורמים.[3] הקיום של החורים השחורים האקוסטיים אפשרי תאורטית מכיוון שמשוואות התנועה (קינמטיקה) של פונונים בזורמים מושלמים זהות לאלו של שדות (כמו שדה הכבידה) במרחב-זמן.[4] לכן, מערכת שבה יכול להיווצר חור שחור אקוסטי נקראת אנלוגיית כבידה. כמעט כל זורם יכול לשמש ליצירת אופק אירועים אקוסטי, אך הצמיגות והנוכחות של מערבולות ברוב הזורמים מקשה מאוד על גילוי של מאפיינים עדינים כמו קרינת הוקינג.[4][5] לפי אונרו, המדידה של קרינת הוקינג הפונונית היא אתגר לא פשוט, אבל היא צריכה להיות הרבה יותר פשוטה טכנולוגית ממדידת קרינת הוקינג האסטרופיזית, שהתקווה היחידה למדידתה היא על ידי יצירה של חורים שחורים זעירים במעבדה.[3]
מחקרים עכשוויים[עריכת קוד מקור | עריכה]
מערכות זורמים כמעט-מושלמים המוצעות ליצירת חורים שחורים אקוסטיים הן הליום על-נוזלי, גז פרמי מנוון ועיבוי בוזה-איינשטיין. ישנן מערכות נוספות שהן אנלוגיות כבידה שאינן מערכות פונונים בזורם, כמו אור איטי ומערכות יונים.[6] האנלוגיה הראשונה לחור שחור נוצרה רק ב-2009 במערכת של עיבוי בוזה-איינשטיין של הגז האטומי רובידיום.[7] במערכת זו, החור השחור האקוסטי נוצר באמצעות טכניקה של הפעלת פוטנציאל חיצוני על העיבוי. הפוטנציאל החיצוני מאיץ את העיבוי בצורה לא-הומוגנית כך שנוצר גרדיאנט מהירויות זרימה בתחום של זרימה תת-קולית ועל-קולית, ולכן נוצר אופק אירועים אקוסטי שבו מהירות הזרימה שווה למהירות הקול. על ידי שימוש בפוטנציאל עם מינימום, העיבוי נדחה ומתקבלת תופעה של היפוך צפיפות.[7] הכבידה המשטחית וטמפרטורת הוקינג של החור השחור האקוסטי במערכת חושבו תאורטית, אך עדיין לא נעשה ניסיון למדוד את קרינת הוקינג הפונונית. המדענים שיצרו זאת טוענים שהניסוי מתאים למדידת הקרינה והציעו דרך שבאמצעותה ניתן לבצע זאת על ידי יצירת מהוד עבור הפונונים המורכב מזוג של חורים שחורים אקוסטיים.
תאוריה[עריכת קוד מקור | עריכה]


הצגה היוריסטית[עריכת קוד מקור | עריכה]
אנלוגיית החור השחור האקוסטי[עריכת קוד מקור | עריכה]
 ערך מורחב – חור שחור
ערך מורחב – חור שחור
חור שחור הוא עצם שמימי בעל שדה כבידה כה חזק עד ששום גוף, לרבות אור, אינו יכול להתנתק ממנו. אופק האירועים הוא המשטח הדמיוני המפריד בין התחום שממנו האור יכול לברוח, והתחום שבתוכו האור כלוא בתוך החור השחור לעד. נוכל לחשוב על חלקיק אור יחיד (פוטון) המנסה להתקדם בכיוון הבריחה מהחור השחור (ראו איור 1). נתבונן בקטע קטן סביב אופק האירועים של החור השחור: הפוטון שנמצא מימינו יוכל להתקדם ולברוח, אך הפוטון שמשמאלו לא יוכל להתקדם ו"ייסחף" חזרה אל תוך החור השחור. עתה נבנה את האנלוגיה האקוסטית של החור השחור על ידי אנלוגיה לזורם, שבצד אחד זורם שמאלה במהירות הקטנה ממהירות הקול (מהירות תת-קולית) ובצד השני זורם במהירות הגבוהה ממהירות הקול (מהירות על-קולית) . בין צדדים אלה קיים משטח ביניים שעליו מהירות הזרימה שווה בדיוק למהירות הקול והוא מהווה את אופק האירועים האקוסטי. באנלוגיה מוחלטת לפוטון, נחשוב על חלקיק של גל קול (פונון) המנסה להתקדם ימינה בתוך הזורם: גל הקול מתקדם במהירות הקול, ולכן אם הוא נוצר מימין לאופק האירועים הוא יוכל להמשיך להתקדם כנגד הזרם, אך אם הוא נוצר משמאל לאופק האירועים הזרם יהיה חזק מדי והוא יוכל רק "להיסחף" ולסגת שמאלה.
ספקטרום העירורים[עריכת קוד מקור | עריכה]
כדי להראות בצורה היוריסטית איך מתקבלת קרינת הוקינג פונונית מתוך החור השחור האקוסטי, נבחן את האנרגיות (ספקטרום) של העירורים האקוסטיים (הפונונים) בתוך הזורם. נניח שמהירות הזורם ביחס למערכת המעבדה (למשל הצינור שבתוכו מתנועע הזורם) היא המכוונת שמאלה (ראו איור 2). לפני יצירה של פונון, התנע והאנרגיה של מערכת הנוזל הם:
כאשר היא מסת הזורם ו- היא אנרגיית אינטראקציה פנימית כלשהי של הזורם.[8]
אנחנו פועלים בקירוב הלא-יחסותי ולכן ניתן להשתמש בטרנספורמציות גליליי. עתה נניח שמופיע בנוזל פונון עם תנע ואנרגיה (בהתאם ליחס הנפיצה של העירורים במערכת) במערכת המנוחה של הזורם. נשים לב שהתנע והאנרגיה של הפונון זהות בכל מערכת ייחוס (הם אינווריאנטים לטרנספורמציות גליליי) משום שהפונון חסר מסה, זאת בדומה ליחסות פרטית שבה מהירות האור זהה בכל מערכת ייחוס. נבטא את התנע והאנרגיה של הזורם במערכת המעבדה לאחר הופעת הפונון באמצעות טרנספורמציית גליליי:
הפרש האנרגיות בין התחלה וסוף במערכת המעבדה יתנו לנו את האנרגיה (ספקטרום) של העירורים במערכת המעבדה:
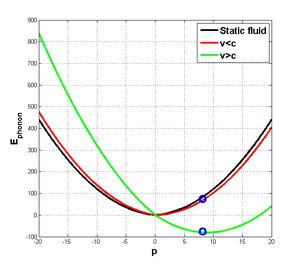
נניח יחס נפיצה ליניארי (מגדיר את מהירות הקול, אך מדויק רק בתנעים נמוכים בדרך כלל) רק כדי שניתן יהיה לראות את התנהגות הספקטרום בצורה סכמתית (ראו איור 3):
- זורם סטטי (גרף שחור) - הספקטרום חיובי ופרבולי, אין העדפה לפונונים בכיוון מסוים.
- זרימה תת-קולית (גרף אדום) - הספקטרום מוטה מעט ימינה. הסיבה לכך היא שישנה העדפה ליצירת פונונים המתקדמים ימינה, כי מחסום האנרגיה ליצירתם קטן עקב תנועת הזורם שמאלה.
- זרימה על-קולית (גרף ירוק) - הספקטרום מוטה ימינה ואף שלילי עבור תחום של תנעים. המשמעות של החלק השלילי בספקטרום היא היכולת ליצור פונונים "בחינם", כלומר ללא צורך בהכנסה של אנרגיה נוספת למערכת. נשים לב שיש צורך להכניס תנע למערכת בצורה כלשהי כדי ליצור פונונים, כך שהתהליך הזה אינו מתרחש באופן ספונטני.
תוצאה זו מתקשרת ישירות למושג של קרינת הוקינג, משום שהדרך ההיוריסטית להבין אותה היא שהתנודות הקוונטיות של הריק יוצרות כל הזמן ובכל מקום זוגות של חלקיקים המופיעים לזמנים קצרים מאוד המוגבלים על ידי עקרון האי-ודאות, ואז מתחברים ומשמידים זה את זה. כאשר זוג של פוטונים נוצר על גבי אופק האירועים היחסותי, לעיתים הם לא יוכלו לחזור אחד לשני ולהיעלם, אלא אחד הפוטונים ייבלע על ידי כוח הכבידה העצום של השחור בעוד שהשני יברח החוצה. כשזה קורה, צופה חיצוני ירגיש קרינה אמיתית, וזוהי קרינת הוקינג. שוב, באנלוגיה האקוסטית, ניתן לראות לפי ספקטרום הפונונים שזה אפשרי ליצור זוג של פונונים מכל צד של אופק האירועים האקוסטי כך שסך כול האנרגיה שלהם יחד תהיה אפס. זו ההצדקה ההיוריסטית לאפשרות לקבל קרינה פונונית מהחור השחור האקוסטי.
הצגה מדויקת[עריכת קוד מקור | עריכה]
פורמליזם הגאומטריה הלורנציאנית[עריכת קוד מקור | עריכה]
הפרעות אקוסטיות המתפשטות בזורם סטטי, הומוגני וחסר צמיגות מתוארות על ידי משוואת הגלים הפשוטה:
כאשר c היא מהירות הקול.[4] ניתן להכליל את התוצאה לזורם לא-הומוגני ולא-סטטי: אם זורם הוא ברוטרופי (צפיפותו תלויה בלחץ בלבד), חסר צמיגות והזרימה חסרת ערבוליות (אבל יכולה להיות תלויה בזמן), אז משוואת התנועה של שדה פוטנציאל המהירות זהה למשוואת התנועה של שדה סקאלרי חסר מסה המתקדם בגאומטריה לורנציאנית מממד (כמו במרחב-זמן). משוואת התנועה היא משוואת הגלים הנתונה על ידי הדלאמבריטאן המוכלל:
תחת הנחות אלה, התפשטות הקול נשלטת על ידי המטריקה האקוסטית . המטריקה האקוסטית מתארת גאומטריה לורנציאנית מממד . המטריקה תלויה אלגברית בצפיפות, במהירות הזרימה ובמהירות הקול המקומית בזורם בצורה:
כאן היא מטריצת היחידה .[4]
תוצאה זו מפתיעה מאוד, משום שעל אף שדינמיקת הזרימה היא ניוטונית, לא-יחסותית ומתרחשת בתוך מרחב אוקלידי שטוח (מופרד הזמן), הפלקטואציות (גלי הקול) נשלטות על ידי גאומטריית מרחב-זמן עקומה (פסואדו-רימנית) מממד . ניתן לבטא את אלמנט האורך (האינטרוול) במקום לבטא את המטריקה:
נשים לב שבדיון זה יש לנו שתי מטריקות שונות:
- המטריקה הפיזית של המרחב-זמן שהיא המטריקה השטוחה הרגילה של מרחב מינקובסקי , כאשר היא מהירות האור. החלקיקים המרכיבים את הזורם מתקיימים במרחב ולכן נצמדים רק למטריקה הפיזית . למעשה, כל תנועת הזורם מנותחת במסגרת לא-יחסותית ולכן ניתן להתייחס למרחב כאוקלידי שטוח.
- ההפרעות האקוסטיות (גלי הקול) מוגדרות על גבי המטריקה האקוסטית ולכן מצומדות רק אליה ולא למטריקה הפיזית .
אופק האירועים האקוסטי מוגדר, כמו ביחסות כללית, על ידי הדרישה לגבול של התחום שממנו הגאודזיות דמויות-הזמן (הפונונים) לא יכולות לברוח לאינסוף העתידי. על ידי בחירת טרנספורמציית קואורדינטות מתאימה ניתן להגיע לשוויון (עד כדי פקטור קונפורמי) בין המטריקה האקוסטית למטריקת שוורצשילד של החור השחור:
השוויון (עד כדי פקטור קונפורמי) הוא מספיק בשביל להגדיר על גבי אופק האירועים את הכבידה המשטחית ואת קרינת הוקינג. הסיבה היא שהכבידה המשטחית וקרינת הוקינג הם אינווריאנטים קונפורמיים.[4] מכאן ניתן לקבל שבמקרה של זרימה יציבה (סטציונרית) הכבידה המשטחית (האקוסטית) של אופק האירועים האקוסטי ניתנת על ידי הפרש הנגזרות הנורמליות לאופק האירועים של מהירות הקול הלוקאלית ומהירות הזרימה:
אופק האירועים האקוסטי יפלוט קרינת הוקינג בצורת קרינת גוף שחור פונונית בטמפרטורה:[4]
תפקיד האנלוגיה האקוסטית בפיזיקה[עריכת קוד מקור | עריכה]
תחת מספר הנחות, גלים אקוסטיים בזורמים חסרי צמיגות יכולים להיות מתוארים על ידי משוואות תנועה של גאומטריה לורנציאנית. באופן מסורתי, גאומטריות לורנציאניות היו מעניינות רק בתחום תאוריית הכבידה של אלברט איינשטיין. אנלוגיות הכבידה האקוסטיות מרחיבות את היריעה התאורטית לתחומים פיזיקליים נוספים. התוצאה המעניינת ביותר היא שהפיזיקה הניוטונית הלא-יחסותית של זורמים שבה מושגי המרחב והזמן מופרדים לחלוטין, עדיין מתארת גלים אקוסטיים המצומדים לגאומטריה לורנציאנית של מרחב-זמן. תוצאה זו מכריחה אותנו לנתח את הפיזיקה של החורים השחורים בשביל להפריד את המאפיינים שהם ייחודיים ליחסות כללית והמאפיינים הגנריים לכל גאומטריה לורנציאנית. האנלוגיה האקוסטית משקפת בדיוק "חצי" מהיחסות הכללית, שהיא הקינמטיקה שמגדירה הגאומטריה הלורנציאנית. ה"חצי" השני, שלא מתבטא באנלוגיה האקוסטית, היא הדינמיקה שמגדירות משוואות איינשטיין ביחסות הכללית. המסקנה החשובה ביותר היא שקרינת הוקינג הנפלטת מאופק האירועים היא אפקט קינמטי לחלוטין שמתרחש בכל גאומטריה לורנציאנית שמוגדר בה אופק אירועים.[4]
קשיים תאורטיים[עריכת קוד מקור | עריכה]
בנוסף, כבר בתחילת דרכה של תאוריית קרינת הוקינג זיהו בעיה פוטנציאלית בשיטת החישוב. החישוב מתבסס על נכונות תורת השדות הקוונטית על רקע של מרחב עקום ובמרחבים קצרים שרירותית (או אנרגיות גבוהות שרירותית). ביחסות הכללית, אם נבחן את חבילת הגלים הסופית (פוטון) שבורחת לאינסוף מהחור השחור ונעקוב אחריה אחורה בזמן, נקבל שאורך הגל שואף לאפס על אופק האירועים (תדירות הגל היא הגודל הפיזיקלי שאינו משתנה). באופן עקרוני, כל פיזיקה בלתי ידועה שמעבר לסקאלת פלאנק יכולה להשפיע משמעותית על תהליך קרינת הוקינג. לכן, בעיה זו נקראת הבעיה הטראנס-פלאנקיאנית.[9]
פן ניסיוני[עריכת קוד מקור | עריכה]
יצירת חור שחור אקוסטי[עריכת קוד מקור | עריכה]
לכידה של עיבוי בוז-איינשטיין[עריכת קוד מקור | עריכה]
 ערך מורחב – קירור באמצעות לייזרים
ערך מורחב – קירור באמצעות לייזרים
על מנת ליצור עיבוי בוז-איינשטיין, בחירה נפוצה היא שימוש בגז של אטומי רובידיום, מכיוון שמומנט הדיפול של הרובידיום הוא גדול בהשוואה לגזים אחרים ולכן הוא מתאים לשימוש במלכודת אלקטרומגנטית. אטומי הרובידיום הם כבדים ונוטים להתמצק במגע עם חומר אחר או זה עם זה. לכן, מנדפים אותם ושומרים אותם בצפיפות נמוכה במלכודת אופטית, הרחק מחומר מוצק אחר ועם קצב התנגשויות נמוך בינם לבין עצמם.
יצירת אופק האירועים האקוסטי[עריכת קוד מקור | עריכה]
כדי ליצור את אופק האירועים האקוסטי, יש ליצור גרדיאנט מהירויות בתוך העיבוי בוזה-איינשטיין כך שנקבל התפלגות מרחבית של מהירויות תת-קוליות ועל-קוליות. לשם כך, יש להפעיל פוטנציאל חיצוני תלוי בזמן על העיבוי, למשל על ידי לייזרים או שדות מגנטיים משתנים.
שיטת היפוך הצפיפות[עריכת קוד מקור | עריכה]
בשיטת היפוך הצפיפות, העיבוי זורם לתוך נקודת מינימום הפוטנציאל ומאיץ אל צדו השני. בנקודת המינימום הזרימה היא המהירה ביותר ולכן הצפיפות שם נמוכה כפי שמוכתב על ידי משוואת הרציפות. אם הפוטנציאל היה חזק מספיק כדי להאיץ את הזרימה למהירות על-קולית, נקבל שני אופקים אקוסטיים (אנלוגי לחור שחור וחור לבן יחסותיים) שיכולים לשמש כמהוד אקוסטי ולעזור למדוד את הפונונים.[7]
אתגרים במדידת קרינת הוקינג פונונית[עריכת קוד מקור | עריכה]
הפרעות מעירורים אלמנטריים[עריכת קוד מקור | עריכה]
על מנת לחזות ניסיונית בקרינת הוקינג הפונונית במעבדה, יש להעלים את כל המקורות לאי-יציבויות שיוכלו למסך את התופעה. במערכות של זורמים החיכוך מהווה בעיה, ועבור מערכת של על-נוזל או עיבוי בוזה-איינשטיין יש לבחון את תנאי המהירות הקריטית של לנדאו, שקובע החל מאיזו מהירות יש לזורם מספיק אנרגיה ותנע כדי ליצור עירורים אנרגטיים (כמו פונונים) במערכת שמהווים את הפסדי האנרגיה של המערכת (חיכוך) במגע עם הדפנות של המערכת.[8] הדופן יכולה להיות גם מלכודת אלקטרומגנטית במקרה הנפוץ של שימוש בעיבוי בוזה-איינשטיין. על מנת ליצור חור שחור אקוסטי יש להגיע למצב של זרימה על-קולית ובמקרה זה העירורים הרבים יגרמו להפסדים שלא יאפשרו לשמור על מהירות הזרימה, או ליצירה של רוטונים (סוג של עירור של הליום על-נוזלי) ומערבולות מקוונטטות. בכל מקרה, העירורים יקשו על שמירה על אופק האירועים לאורך זמן, יצירה של קרינת הוקינג או גילויה. שיטות התמודדות עם בעיות אלה:[9]
- במערכת של הליום על-נוזלי - ניתן לבצע אנלוגיה השונה מפונונים בזורם, ולהשתמש בריפלונים (עוד סוג של עירור של הליום על-נוזלי) בממשק בין פאזות A ו-B של הליום-3.
- במערכת של עיבוי בוזה-איינשטיין - על מנת למנוע את היווצרותן של המערבולות הקוונטיות היא להשתמש בקונפיגורציות חד-ממדיות וצרות של העיבוי. אם המימד הניצב לזרימה של העיבוי יהיה קטן מאורך הריפוי, לא יהיה מספיק מקום להיווצרות המערבולות.
רעש תרמי[עריכת קוד מקור | עריכה]
הצבת הקבועים המספריים בנוסחה לטמפרטורת הוקינג הפונונית תיתן:[4]
ניתן לראות מכאן שטמפרטורת הוקינג שתתקבל היא נמוכה מאוד ומסדר גודל של , שזהו גם סדר הגודל של הטמפרטורות אליהן מגיעים במערכות אלו. אם האנרגיה התרמית של המערכת תהיה גדולה מהאנרגיה האפקטיבית של קרינת הוקינג הפונונית (פליטת פונונים עם התפלגות ספקטראלית של קרינת גוף שחור), לא ניתן יהיה להבחין בפונונים של קרינת הוקינג מבין רעשי הרקע. אבל, כפי שאונרו כתב במאמרו,[3] זה עדיין יהיה קל יותר טכנולוגית מיצירה של חורים שחורים זעירים (יחסותיים) במעבדה.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- קבוצת הפיזיקה האטומית בטכניון
- 100 הכתבות הטובות של 2009, #79: "חור שחור אקוסטי נוצר במעבדה", מגזין Discover
- "אנלוגיות כבידה", ניתוח מתמטי מפורט
 הרצאה מוקלטת של פרופ' ג'ף סטיינהאור על יצירת חור שחור אקוסטי בעיבוי בוזה-איינשטיין, סרטון באתר יוטיוב
הרצאה מוקלטת של פרופ' ג'ף סטיינהאור על יצירת חור שחור אקוסטי בעיבוי בוזה-איינשטיין, סרטון באתר יוטיוב
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ G. Jannes, “Emergent gravity: the BEC paradigm,” Ph.D thesis, Department of Theoretical Physics, Complutense University of Madrid, page 12, Arxiv preprint arXiv:0907.2839 (2009).
- ^ אישוש להוקינג: חור שחור מלאכותי מאשש באופן כמותי את הטמפרטורה והאופי התרמי של קרינת הוקינג, באתר הידען, יוני 6 2019
- ^ 1 2 3 W. G. Unruh, “Experimental black hole evaporation,” Phys. Rev. Lett. 46, 1351 (1981).
- ^ 1 2 3 4 5 6 7 8 M. Visser, “Acoustic black holes: Horizons, ergospheres, and Hawking radiation,” Classical and Quantum Gravity 15, 1767 (1998) arXiv:gr-qc/9712010
- ^ G. Jannes, “Emergent gravity: the BEC paradigm,” Ph.D thesis, Department of Theoretical Physics, Complutense University of Madrid, page 34, Arxiv preprint arXiv:0907.2839 (2009).
- ^ B. Horstmann, R. Schützhold, B. Reznik, S. Fagnocchi, and J. I. Cirac, “Measurement of Hawking Radiation with Ions in the Quantum Regime,” Arxiv preprint arXiv:1008.3494, 2010.
- ^ 1 2 3 O. Lahav, A. Itah, A. Blumkin, C. Gordon & J. Steinhauer, “A sonic black hole in a density-inverted Bose–Einstein condensate” Phys. Rev. Lett. 105, 240401 (2009) Arxiv preprint arXiv:0906.1337.
- ^ 1 2 Y. Yamamoto, "QIS385 Bose-Einstein Condensation and Matter-Wave Lasers, Chapter 5: Superfluidity” FIRST Quantum Information Processing Project
- ^ 1 2 Carlos Barceló, Stefano Liberati, and Matt Visser, "Analogue Gravity" gr-qc/0505065






















![{\displaystyle ds^{2}\equiv g_{\mu \nu }dx^{\mu }dx^{\nu }={\frac {\rho }{c}}\left[-c^{2}dt^{2}+\left(dx^{i}-v^{i}dt\right)\delta _{ij}\left(dx^{j}-v^{j}dt\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7932f08005e500e23c9c4e5918ca05a46b619e76)








![{\displaystyle T_{H}=\left(1.2\cdot 10^{-9}{\mbox{K}}\cdot {\mbox{m}}\right)\left[{\frac {c}{1000{\mbox{m}}\cdot {\mbox{s}}^{-1}}}\right]\left[{\frac {1}{c}}{\frac {\partial \left(c-v_{\perp }\right)}{\partial n}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f3b41b55562f274048c50cfaeba320108618ed4)


