תבניות בטבע


תבניות בטבע הן תופעות של סדירות צורנית אשר מופיעות בטבע. התבניות האלו ניכרות בהקשרים שונים, ולעיתים ניתן למדל אותן באופן מתמטי. בין התבניות הטבעיות נכללות סימטריות, עצים, ספירלות, נפתולים, גלים, קצפים, ריצופים, סדקים ופסים. הפילוסופיה היוונית הקדומה עסקה בחקר תבניות: אפלטון, פיתגורס ואמפדוקלס ניסו להסביר את קיומו של סדר בטבע. ההבנה המודרנית של התבניות האלו התפתחה בהדרגה לאורך זמן.
במאה ה-19 חקר הפיזיקאי הבלגי ז'וזף פלאטו קרומי סבון, ובעקבות כך ניסח את רעיון המשטח המינימלי. הביולוג והאמן הגרמני אֶרְנְסְט הֶקֶל צייר מאות אורגניזמים ימיים על מנת להדגיש את הסימטריה שלהם. הביולוג הסקוטי דארסי וונטוורת תומפסון החל את המחקר של דפוסי צמיחה, בצמחים כמו גם בבעלי חיים, והראה כי ניתן להסביר צמיחה ספירלית באמצעות משוואות פשוטות. במאה ה-20 חזה המתמטיקאי הבריטי אלן טיורינג את קיומם של מנגנוני מורפוגנזה היוצרים תבניות של חברבורות ופסים. הביולוג ההונגרי אריסטיד לינדנמאייר, ביחד עם המתמטיקאי הצרפתי-אמריקאי בֶּנוּאָה מנדֶלבּרוֹט, הראו כיצד המתמטיקה של פרקטלים מסוגלת לייצר דפוסי גדילה המופיעים בעולם הצומח.
המתמטיקה, הפיזיקה והכימיה מסבירות תבניות בטבע ברמות שונות. תבניות בעולם החי והצומח מוסברות באמצעות התהליכים הביולוגיים של ברירה טבעית וברירה זוויגית. מחקרים העוסקים בהיווצרות תבניות משתמשים במודלים ממוחשבים כדי ליצור הדמיות של מגוון רחב של תבניות.
היסטוריה[עריכת קוד מקור | עריכה]

הפילוסופיה של יוון העתיקה הקדימה את המחשבה המודרנית בניסיונותיה להסביר את הסדר המופיע בטבע. אפלטון (427–347 לפנה"ס לערך) טען לקיומן של תכונות אוניברסליות בעבודותיו על תבניות טבעיות. הוא טען כי אלו מורכבות מצורות אידיאליות (εἶδος, "צורה"), שמהן נגזרים עצמים פיזיים המהווים העתקים לא מושלמים שלהן. לפיכך, פרח יכול להיות עגול, אולם הוא לעולם לא יהיה עיגול מתמטי מושלם. פיתגורס הסביר כי תופעת התבניות בטבע, בדומה להרמוניות מוזיקליות, נובעת ממספרים, שאותם הוא החשיב בתור הגורם הבסיסי לכלל הקיום. אמפדוקלס חזה במידה מסוימת את ההסבר האבולוציוני של דרווין למבניהם של אורגניזמים.
ב-1202 לאונרדו פיבונאצ'י (1170–1250 לערך) הציג לעולם המערבי את סדרת פיבונאצ'י ב"ספר החשבונייה" (Liber Abaci). פיבונאצ'י הציג דוגמה ביולוגית (שאינה ריאליסטית), בגידול המספרי של אוכלוסיית ארנבים תאורטית.[1] ב-1917 פרסם דארסי וונטוורת תומפסון (אנ') (1860–1948) את ספרו "על גידול וצורה" (On Growth and Form), המכיל תיאור קלאסי של פילוטקסיס (אופן הסידור של עלים על גבעול צמח) וסדרת פיבונאצ'י, והקשר המתמטי בין תבנית הצמיחה הספירלית של צמחים. הוא הראה כי ניתן לתאר באמצעות משוואות פשוטות את כל תבניות הצמיחה הספירליות המסובכות למראה של קרני בעלי חיים וקונכיות רכיכות.[2]
הפיזיקאי הבלגי ז'וזף פלאטו (אנ') (1801–1883) ניסח את הבעיה המתמטית של קיום משטח מינימלי לגבול נתון, הקרויה על שמו. הוא חקר לעומק קרומי סבון, וניסח את חוקי פלאטו, המתארים את המבנים הנוצרים על ידי קרומים בקצף.
הפסיכולוג הגרמני אדולף צייזינג (אנ') (1810–1876) טען כי יחס הזהב מובע בסידור של חלקי הצמח השונים, בשלדים של בעלי חיים והתבנית המסתעפת של העורקים והעצבים שלהם, ובגאומטריה של גבישים.
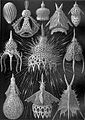
ארנסט הקל (1834–1919) יצר איורים יפהפיים של אורגניזמים ימיים, בייחוד קרנוניות (רדיולריה), תוך הדגשת הסימטריה שלהם, על מנת לתמוך ברעיונות האבולוציוניים הפסאודו-דרוויניסטיים שלו.
הצלם האמריקאי וילסון בנטלי (1865–1931) צילם את תמונת המיקרוסקופ הראשונה של פתית שלג ב-1885.

ב-1952, אלן טיורינג (1912–1954), המוכר בעיקר מעבודותיו במדעי המחשב ושבירת-צפנים, כתב את "הבסיס הכימי של מורפוגנזה", ניתוח של המנגנונים שצריכים להתקיים על מנת שייווצרו תבניות ביצורים חיים, באמצעות התהליך המכונה "מורפוגנזה". הוא חזה את קיומן של תגובות כימיות מחזוריות, וספציפית את ריאקציית בלוסוב-ז'בוטינסקי (Belousov–Zhabotinsky (אנ')). טיורינג הציע כי מנגנוני הפעלה-עיכוב כאלו יכולים לייצר תבניות של פסים וחברבורות אצל בעלי חיים, ולתרום להיווצרות התבניות הספירליות המופיעות בפילוטקסיס של צמחים.
ב-1968 פיתח הביולוג התאורטי ההונגרי אריסטיד לינדנמאייר (אנ') (1925–1989) פיתח את מערכת לינדנמאייר (מערכת-L) – מערכת דקדוק פורמלית שניתן למדל באמצעותה תבניות גדילה של צמחים בסגנון פרקטלי. למערכות-L יש אלפבית של סמלים שניתן לשלבם באמצעות כללי ייצור (Production rules) על מנת ליצור מחרוזות ארוכות יותר של סמלים, ומנגנון לתרגום המחרוזות הללו למבנים גאומטריים. ב-1975, לאחר מאות שנים שבמהלכן המתמטיקה של התבניות קודמה באיטיות על ידי גוטפריד לייבניץ, גאורג קנטור, הלגה פון קוך, ואצלב שרפינסקי ואחרים, כתב בנואה מנדלברוט את מאמרו המפורסם "כמה ארוך הוא החוף של בריטניה? דמיון עצמי סטטיסטי והממד הפרקטלי", אשר גיבש את המחשבה המתמטית הקיימת לכדי רעיון הפרקטל.

בתבניות האבסטרקטיות שניתן לראות בעולם החי, כגון על סחלבים, יונקי דבש, וזנב הטווס, ישנו יופי של צורה, צבע, ודפוס, שאמנים מתקשים לחקות. ישנן רמות שונות של גורמים ליופי הנחזה בטבע, בעיקר במתמטיקה המסדירה את התבניות הנוצרות, ובעקרונות של ברירה טבעית, המסדירה את התפתחות התבניות המופיעות אצל יצורים חיים.
המתמטיקה שואפת לגלות ולהסביר תבניות מופשטות או סדירויות מכל הסוגים. ניתן להסביר תבניות ויזואליות בטבע באמצעות תורת הכאוס, פרקטלים, ספירלות לוגריתמיות, טופולוגיה ותבניות מתמטיות נוספות. לדוגמה, באמצעות מערכות-L ניתן ליצור מודלים משכנעים לתבניות שונות של צמיחת עצים.

חוקי הפיזיקה מיישמים את ההפשטות המתמטיות על העולם האמיתי, תכופות בהתבסס על ההנחה כי הוא מושלם. לדוגמה, גביש שאין לו אף פגם מבני (כגון נקעים) והוא סימטרי לחלוטין, הוא גביש מושלם. מושלמות מתמטית מוחלטת יכולה רק לתת הערכה מקורבת לעצמים אמיתיים. התבניות הנצפות בטבע נשלטות על ידי חוקי הטבע; למשל, דינמיקה של נוזלים יכולה להסביר את היווצרותם של נפתולים.
בביולוגיה, ברירה טבעית יכולה להוביל להתפתחותם של תבניות אצל יצורים חיים מכמה סיבות, בהן הסוואה, ברירה זוויגית, וסוגים שונים של איתות דוגמת חקיינות או סימביוזת ניקוי (אנ') . אצל צמחים, הצורות, הצבעים והתבניות של פרחים דוגמת השושן התפתחו על מנת לייעל האבקה על ידי חרקים (צמחים אחרים עשויים לעבור האבקה על ידי רוח, ציפורים, או עטלפים) דבורת הדבש האירופית, וחרקים מאביקים אחרים, נמשכים לא רק לריח ולתגמול של צוף עשיר בסוכר ולאבקנים אכילים, אלא גם לדוגמאות הרדיאליות בצבען וצורתן המוצגות על הפרחים, ואשר משמשות כמנחי-צוף שניתן לראותן למרחק רב.
סוגי תבניות[עריכת קוד מקור | עריכה]
סימטריה[עריכת קוד מקור | עריכה]
סימטריה קיימת באופן נרחב בעולם החי והצומח. אצל בעלי חיים ישנה בעיקר סימטריה דו-צדדית (סימטריית מראה), כמו גם אצל עלים של צמחים, ופרחים מסוימים דוגמת סחלבים. אצל צמחים מופיעה לעיתים קרובות סימטריה רדיאלית או סיבובית, כמו אצל פרחים רבים וקבוצות מסוימות של בעלי חיים כגון שושנות ים. ניתן לראות סימטריה מחומשת אצל פרטים מסוימים ממערכת קווצי העור, הכוללת כוכבי ים, קיפודי ים, וחבצלות ים.
מחוץ לעולם החי, סימטריה משושה מרשימה במיוחד מצויה בפתיתי שלג: כל פתית הוא ייחודי, ומבנהו מגלם מעין תיעוד של התנאים המשתנים במהלך התגבשותו, כאשר תבנית הצמיחה היא כמעט זהה בין שש הזרועות. לגבישים יש מגוון רחב של סוגי סימטריה וצורת גביש; הם עשויים להיות קובייתיים או אוֹקטָהדרליים, אך גבישים אמיתיים אינם יכולים להפגין סימטריה מחומשת (שלא כמו גבישים כמו-מחזוריים, או קווזיפריודיים). ניתן לראות סימטריה סיבובית בקני מידה שונים בעצמים דוממים, כמו תבנית ההתזה דמוית-הכתר הנוצרת כאשר טיפה נופלת לתוך אגם, או בצורה הספרואידית של פלנטה כגון שבתאי, כמו גם בצורת הטבעות שסביבה.
ישנם מגוון גורמים היוצרים סימטריה. סימטריה רדיאלית מתאימה לאורגניזמים כמו שושנות ים, שצורתם הבוגרת נייחת: מזון ואיומים עשויים להגיע מכל כיוון. אולם אצל בעלי חיים שנעים בכיוון מסוים, ישנם בהכרח צד עליון וצד תחתון, כמו גם קדמי ואחורי, ושמאלי וימני. הראש מתמחה באברי חישה ופה (צֶפָליזציה (אנ')), והגוף מקבל סימטריית מראה (אף שהדבר אינו הכרחי באיברים הפנימיים). תמוה יותר מאלו הוא הגורם לסימטריה המחומשת המופיעה אצל קווצי העור. קווצי עור קדומים היו בעלי סימטריית מראה, דבר הניכר עדיין בזחליהם. סומראל וריי (Sumrall and Wray) טוענים כי ישנם גורמים התפתחותיים ואקולוגיים באובדן הסימטריה הקודמת.
-
חיות רבות, כגון הטיגריס הזה, מפגינות סימטריית מראה.
-
לקווצי העור, כגון כוכב-הים הזה, יש סימטריה מחומשת.
-
לפתיתי שלג יש סימטריה משושה.
-
כל פתית שלג הוא ייחודי, אך סימטרי.
-
צורת גביש קובייתית בפלואוריט
-
תבנית ההתזה של מים היא קירוב של סימטריה רדיאלית.
-
צורת גביש דודקהדרונית בגארנט
-
לשושנות ים יש סימטריה סיבובית.
עצים, פרקטלים[עריכת קוד מקור | עריכה]
פרקטלים הם מבנים מתמטיים איטֶרָטיביים בעלי דמיון עצמי (אנ') אינסופי וממד פרקטלי. חזרה-עצמית אינסופית אינה אפשרית בטבע, כך שכל המבנים הפרקטליים הם למעשה קירובים בלבד. לדוגמה, עליהם של שרכים או סוככיים הם בעלי דמיון עצמי (מנוצים (אנ')) רק 2, 3 או 4 פעמים. דגמי צמיחה שרכיים מתרחשים אצל צמחים ובעלי חיים, ביניהם חיטחבים, אלמוגים, הידרתים כגון שרך האוויר (Sertularia argentea (אנ')), ובתופעות כמו פריקה חשמלית (אנ'). באמצעות פרקטלים של מערכות-L ניתן למדל תבניות שונות של צמיחת עצים באמצעות שינויים במספר פרמטרים קטן, כגון זווית הסתעפות, המרחק (אורך גבעול) בין צמתים או נקודות הסתעפות, ומספר ההסתעפויות מכל נקודה כזו.
תבניות דמויות-פרקטל מופיעות באופן נרחב בטבע בתופעות כגון עננים, מערכות נהרות, קווי שבר גאולוגיים, הרים, קווי חוף, צבעי בעלי חיים, פתיתי שלג, גבישים, סיעוף כלי דם, וגלי מים.
-
עלה של סיָיגית היערות (Anthriscus sylvestris), מנוצה 2 או 3 פעמים, לא באופן אינסופי
-
ספירלות פרקטליות: כרובית אלמוגים מפגינה דמיון עצמי בצורתה
-
עצים: צורות ליכטנברג (אנ'): התפלגות דיאלקטרית במתח גבוה בגוש פולימר אקרילי
-
תבניות הפשרה פרקטליות על מאדים
ספירלות[עריכת קוד מקור | עריכה]
ספירלות נפוצות בקרב צמחים ובעלי חיים מסוימים, בעיקר רכיכות. לדוגמה, אצל הנאוטילוס (שייטניים), רכיכה ממחלקת הסִילוֹנִיּוֹת, כל תא בקונכייה הוא העתק מקורב של התא שאחריו, בשינוי קנה מידה קבוע, והתאים מסודרים בספירלה לוגריתמית. בעקבות ההבנה המודרנית של פרקטלים, ניתן לראות את ספירלת הגדילה כמקרה מיוחד של דמיון עצמי.
ניתן לראות ספירלות אצל צמחים בפילוטקסיס שלהם, סידור העלים על הגבעול, וכן בסידור של חלקים אחרים[3] דוגמת מבני פרחים או זרעים מרוכבים, כגון החמנית, מבני פרי כגון האננס וסלאק (דקל פרי הנחש), או בתבנית הקשקשים המופיעה על איצטרובלים, שבה כמה ספירלות אשר הולכות עם ונגד כיוון השעון. ניתן להסביר את הסידורים האלו בכמה רמות – מתמטיקה, פיזיקה, כימיה וביולוגיה. ניתן לייצר מתמטית ספירלות פילוטקסיות באמצעות יחסי פיבונאצ'י: רצף פיבונאצ'י מתחיל במספרים 1, 1, 2, 3, 5, 8, 13... (כאשר כל מספר הוא סכום המספרים לפניו). לדוגמה, כאשר צד העלה מתחלף לאורך גבעול, סיבוב אחד של הספירלה נוגע בשני עלים, כך שיחס התבנית הוא 1/2. בלוּז היחס הוא 1/3; במשמש הוא 2/5; באגס הוא 3/8; בשקד הוא 5/13. בפילוטקסיס עגול (דִיסקוּס), כמו אצל החמנית וחרצית הבר, הפרחים הקטנים מסודרים בספירלת פֶרְמָה (אנ') (או ספירלה פרבולית) עם מספור פיבונאצ'י, לפחות כאשר הפרח בוגר וכל הרכיבים זהים בגודלם. יחסי פיבונאצ'י הם קירוב לזווית הזהב, °137.508, המגדירה את הקימור של ספירלת פרמה.
מנקודת מבט פיזיקלית, ספירלות הן סידור ברמת האנרגיה הנמוכה ביותר אשר נובעות באופן ספונטני מתהליכי סידור-עצמי במערכות דינמיות. מנקודת מבט כימית, ניתן לייצר ספירלה באמצעות תהליך ריאקציה-דיפוזיה (אנ') המערב הן הפעלה והן עיכוב. הפילוטקסיס מבוקר על ידי חלבונים אשר שולטים בריכוז של ההורמון הצמחי אוקסין, שמפעיל את הגדילה של רקמה יוצרת (meristem), נוסף על מנגנונים נוספים לשליטה בזווית היחסית של הניצנים סביב הגבעול. מנקודת מבט ביולוגית, ישנה העדפה של ברירה טבעית לסידור של עלים כך שיהיו רחוקים ככל הניתן זה מזה בכל שטח נתון, משום שסידור כזה מגדיל את הגישה למשאבים, בייחוד אור שמש לפוטוסינתזה.
-
ספירלת פיבונאצ'י
-
כבש גדול-קרניים (כבש הרים) (Ovis canadensis)
-
ספירלות: פילוטקסיס של אלווי רב-עלים (Aloe polyphylla)
-
ספירלת הגדילה הלוגריתמית של קונכיית הנאוטילוס
-
ספירלת פרמה: מבנה זרעים של חמנית מצויה (Helianthus annuus)
-
ספירלות פיבונאצ'י מרובות בחתך רוחבי של כרוב אדום
-
קונכייה של שבלול רומי, בה ניתן לראות את המבנה הספירלי-בורגי מכמה זוויות.
כאוס, זרימה ונפתולים[עריכת קוד מקור | עריכה]
במתמטיקה, מערכת דינמית היא כאוטית אם היא רגישה (מאוד) לתנאי התחלה (מה שמכונה "אפקט הפרפר"), ומציגה את התכונות המתמטיות של ערבוב טופולוגי ומסלולים מחזוריים צפופים.
כמו פרקטלים, תורת הכאוס משפיעה באופן גורף על תבניות בטבע. ישנו קשר בין כאוס ופרקטלים – ישנו ממד פרקטלי למושכים מוזרים במערכות כאוטיות. לאוטומטים תאיים מסוימים – מערכות פשוטות של חוקים מתמטיים אשר מייצרים תבניות – יש התנהגות כאוטית, דוגמת חוק 30 של סטיבן וולפרם.
שדרות ערבולים הן תבניות מזגזגות של מערבולות אשר נוצרות כתוצאה מהפרדת זרימה של זורם כגון מים או אוויר שחולף על פני גוף חוסם. בזרימה שכבתית (למינרית) ההפרעות מתחילות כאשר גודל הגוף החוסם או מהירות הזרימה גדלים מספיק ביחס לצמיגות של הזורם.
נפתולים הם עיקולים מפותלים בנהרות או ערוצים אחרים, אשר נוצרים כאשר זורם כלשהו – לרוב מים – זורמים מסביב לעיקול. מרגע שהמסלול מתעקם אפילו במעט, הגודל והעקמומיות של כל לולאה יגדלו, משום שזרימה הליקלית סוחפת חומרים כגון חול וחצץ לאורך הנהר לצד הפנימי של העיקול. הצד החיצוני של העיקול נותר נקי ולא מוגן, כך שהסחיפה מתגברת, ובתורה מגבירה עוד יותר את הנפתוליות בלולאת פידבק חיובי מתמדת.
-
כאוס: שדרת ערבול של עננים
-
נפתולים: צלקות נפתולים מרשימות ואגמים דמויי סהר במישור ההצפה של הריו נגרו, כפי שנצפה מהחלל
-
נפתולים: זחילת נחש מתפתלת
-
נפתולים: אלמוג מוח סימטרי
גלים, דיונות[עריכת קוד מקור | עריכה]
גל הוא הפרעה אשר נושאת עמה אנרגיה. גלים מכניים נעים בתווך – אוויר או מים – וגורמים לתנודות בתווך כאשר הם עוברים בו. גלי רוח הם גלים בפני השטח של ים, אשר יוצרים את התבנית הכאוטית האופיינית לכל גוף מים גדול, אף שניתן לחזות את ההתנהגות הסטטיסטית שלהם באמצעות מודלים של גלי רוח. כאשר גלי מים או אוויר חולפים מעל חול, הם יוצרים תבניות אַדְוָה. כשרוחות נושבות מעל גופי חול גדולים, הן יוצרות דיונות, לפעמים בשדות דיונות גדולים כמו אלו המופיעים במדבר טקלה מקאן בסין. דיונות נוצרות במגוון תבניות, ביניהן חרמשים, קווים ישרים ארוכים מאוד, כוכבים, כיפות, פרבולות, וצורות 'סיף' (חרב) אורכיות.
דיונות ברחן (סהר) נוצרות בהשפעת רוח על חול מדברי; שתי קרני הסהר ומשטח ההחלקה (slip face) פונים עם כיוון הרוח. חול נושב על המשטח שפונה כנגד הרוח, אשר יוצר זווית של כ-°15 עם המשטח האופקי, ונופל על משטח ההחלקה, היכן שהוא מצטבר עד כדי זווית השיפוע הטבעי של החול, שהיא כ-°35. כאשר משטח ההחלקה עובר את זווית השיפוע הטבעי, החול מתמוטט ונוצרת מפולת, שהיא התנהגות לא-ליניארית: התוספת המצטברת של כמויות קטנות של חול לא משפיעה בהתחלה, ואז כמות קטנה נוספת של חול לפתע גורמת להתמוטטות של כמות גדולה. מלבד אי-ליניאריות זו, דיונות ברחן מתנהגות באופן דומה למדי לגל סוליטון.
-
גלים: גל נשבר בשובל של ספינה
-
דיונות: דיונות חול במדבר טקלה מקאן, כפי שנצפה מהחלל
-
דיונות: דיונת ברחן (סהר)
בועות, קצף[עריכת קוד מקור | עריכה]
בועת סבון יוצרת ספֵירה, שטח עם גודל מינימלי – פני השטח הקטנים ביותר האפשריים לנפח שהם מקיפים. שתי בועות יחדיו יוצרות צורה מורכבת יותר: פני השטח החיצוניים של שתי הבועות הם כדוריים; ביניהם מחבר משטח כדורי קטן יותר, שכן הבועה הקטנה יותר מתבלטת מעט לתוך הגדולה.
קצף הוא מסה של בועות; קצפים מחומרים שונים קיימים בטבע. קצפים המורכבים מקרומי סבון מצייתים לחוקי פלאטו, אשר מגדירים כי שלושה קרומי סבון ייפגשו בכל קצה ב-°120, וארבעה קצוות ייפגשו בכל קודקוד בזווית הארבעונית (טטרהדרונית) של כ-°109.5. חוקי פלאטו דורשים כי קרומי הסבון יהיו חלקים ורציפים, ובעלי עקמומיות ממוצעת קבועה בכל נקודה. לדוגמה, קרום יכול להיוותר שטוח כמעט לחלוטין בממוצע, על ידי עיקומו למעלה בכיוון אחד (למשל שמאל-ימין) ועיקומו למטה בכיוון אחר (למשל קדימה-אחורה). ניתן להשתמש במבני גודל מינימלי כאוהלים. ב-1887, לורד קלווין זיהה את הבעיה של הדרך היעילה ביותר לדחוס תאים בעלי נפח דומה כקצף; הפתרון שהוא הציע השתמש רק במוצק אחד, התמניון הקטום הריבועי (Bitruncated cubic honeycomb), עם פני שטח בעלי עקמומיות נמוכה מאוד כדי להתאים לחוקי פלאטו. פתרון טוב יותר נמצא רק ב-1993, כאשר דניס ווירה ורוברט פלן הציעו את מבנה ווירה-פלן; מרכז ענפי ספורט המים הלאומי בבייג'ינג אימץ את המבנה הזה בבניית הקיר החיצוני שלו באולימפיאדת הקיץ של 2008.
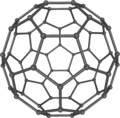
בקנה המידה של תאים חיים, תבניות קצף הן נפוצות למדי; קרנוניות, ספיקולות (Spicule) בשלדים של ספוגיים, שלדים חיצוניים של סיליקופלגלטיים (Silicoflagellates) והשלד הקלציטי של קיפוד הים Cidaris rugosa, כולם מזכירים יציקות מינרליות של גבולות קצף המגלמים את חוקי פלאטו. שלד הקרנונית Aulonia hexagona, שאוירה על ידי הקל, נראית כצורה כדורית אשר מורכבת רק ממשושים, אולם צורה כזו אינה אפשרית מתמטית. מאפיין אוילר מגדיר כי לכל פֵּאוֹן (פוליהדרון) קמור, מספר הפאות ועוד מספר הקודקודים שווה למספר הקצוות ועוד שתיים. כתוצאה מנוסחה זו, כל פאון סגור המורכב ממשושים חייב לכלול בדיוק 12 מחומשים, בדומה לכדור כדורגל, הכיפה הגיאודזית של באקמינסטר פולר, או מולקולת פולרן. ניתן לדמיין זאת בעזרת כך שיריעת משושים היא שטוחה, אולם כל מחומש נוסף מכריח את היריעה להתכופף (יש פחות פינות, כך שהיריעה נמשכת פנימה).
-
הקרנוניות שצייר הקל ב"צורות האומנות של הטבע" (Kunstformen der Natur 1904)
-
ה-Spumellaria (סדרה של קרנוניות) של הקל; השלדים שלהם הם בעלי צורה קצפית.
-
אוהלי קרקס מקורבים בצורתם לרעיון השטח המינימלי.
-
ספירות שוות (בועות גז) בקצף פני שטח.
ריצוף[עריכת קוד מקור | עריכה]
ריצופים או פסיפסים הם תבניות שנוצרות על ידי כיסויו המוחלט של משטח שטוח באריחים החוזרים על עצמם. ישנן 17 חבורות טפט מישוריות (wallpaper groups) של ריצוף. בעוד שאלו נפוצות בעולמות האומנות והעיצוב, בעולם החי קשה למצוא אריחים החוזרים על עצמם בדיוק. בין הדוגמאות המוכרות ישנם התאים בכוורות הנייר של צרעות חברתיות, כמו גם תאי השעווה בחלות הדבש שבונות דבורים. ישנם גם בעלי חיים כגון דגי גרם, זוחלים, והפנגולין, ופירות כמו הסלאק, אשר מוגנים על ידי קשקשים חופפים או אוסטאודרמים: אלו יוצרים יחידות זהות פחות-או-יותר, אף שהקשקשים למעשה משתנים בגודלם באופן רציף. בצמחים ישנו פרח ראש הנחש (Fritillaria meleagris), שעל עלי הכותבת שלו יש דוגמה מרוצפת של משבצות. במבנים של מינרלים שונים יש דוגמאות מוצלחות למערכים תלת־ממדיים החוזרים על עצמם. למרות המספר האדיר של מינרלים מוכרים, ישנן למעשה מעט צורות אפשריות של סידור אטומים בגביש, המוגדרות על ידי מבנה הגביש, המערכת הגבישית, וחבורות סימטריה נקודתיות; לדוגמה, ישנן בדיוק 14 סריגי בְּרָאבֶה ל-7 מערכות הסריגים במרחב התלת-ממדי.
-
גבישים: גבישים קובייתיים של הליט (מלח בישול); המערכת הגבישית הקובייתית, סימטריה גבישית איזומטרית הקסאוקטהדרלית.
-
מערכים: חלת הדבש מציגה תופעת ריצוף טבעית
-
ביסמוט: ניתן לראות את צורת המדרגה של הגביש
-
ריצוף: המראה הפסיפסי של פרח ראש הנחש, Fritillaria meleagris
-
ריצוף: קשקשים חופפים של הליבקית המצויה Rutilus rutilus
-
ריצוף: קשקשים חופפים של פרי הסלאק Salacca zalacca
-
ריצוף: תצורת סלעים נדירה (Tessellated pavement) בחצי האי טסמן, טסמניה
סדקים[עריכת קוד מקור | עריכה]
סדקים הם פתחים ישרים הנוצרים בחומר כדי להקל על עומס. כשחומר אלסטי נמתח או מתכווץ בצורה לא-שווה, הוא מגיע בסופו של דבר לגבול חוזק המתיחה שלו ונכנע בבת אחת לכל הכיוונים, כשבתהליך נוצרים סדקים עם מפרקים של °120, כך ששלושה סדקים נפגשים בכל מפרק. לחלופין, כשחומר לא-אלסטי נכנע, נוצרים סדקים ישרים כדי להקל על העומס. עומס נוסף על אותו הכיוון פשוט יגדיל את הסדקים הקיימים; עומס בזוויות ישרה לקודמים יכול ליצור סדקים חדשים. מכאן שתבנית הסדקים מעידה על מידת האלסטיות של החומר. בחומר סיבי קשוח כמו קליפת עץ אלון, סדקים נוצרים כרגיל כדי להקל על עומס, אך הם אינם גדלים לאורך משום שגדילתם מוגבלת על ידי מקבצים של חומר סיבי חזק ואלסטי. מאחר שלכל סוג עץ יש מבנה תאי ומולקולרי ייחודי, לכל אחד יש תבנית היסדקות שונה בקליפתו.
-
זיגוג לבן על פני חרס ישן המכיל סדקים של בעיקר °90.
-
בוץ לא-אלסטי מתייבש במדבר ראן של קוטש (ערבת מלח בגוג'ראט, הודו) עם סדקים של בעיקר °90.
-
בוץ אלסטי מתייבש בסיציליה עם סדקים של בעיקר °120
-
גזע דקל עם סדקים אנכיים מסתעפים (וצלקות עלים אופקיות)
פסים, חברבורות[עריכת קוד מקור | עריכה]
לנמרים יש חברבורות ולמושית השבע ("פרת משה רבנו") יש נקודות; הפסון המגוון והזברה הם מפוספסים. לתבניות האלו יש הסבר אבולוציוני: יש להן תפקיד בהגברת סיכויי ההישרדות, ודרך כך הרבייה, של צאצאי המין. מטרה אחת של תבניות על בעלי חיים היא הסוואה; למשל, נמר שקשה לראותו צד יותר טרף. מטרה נוספת היא איתות – למשל, למושית השבע יש סיכוי גדול יותר להתחמק מציפורים שצדות בעזרת חוש הראייה, אם יש לה צבעי אזהרה בולטים, והיא גם מרה בטעמה או רעילה, או שהיא מחקה חרקים אחרים שאינם טובים למאכל. ציפור צעירה עשויה לנסות לאכול חרק בעל תבנית אזהרה, אולם היא תנסה זאת רק פעם אחת; מושיות השבע האחרות באזור יוותרו לא מופרעות. הנמרים והחיפושיות הצעירים אשר יורשים גנים שיוצרים נקודות או חברבורות, ישרדו. אולם אף שהטיעונים התכליתיים והאבולוציוניים האלו מסבירים מדוע בעלי חיים אלו זקוקים לתבניות המעטרות אותם, הם אינם מסבירים כיצד התבניות האלו נוצרות.
-
פרפר Colobura dirce
-
זברת גרבי, Equus grevyi
-
דג פסון מגוון, Pygoplites diacanthus
-
נמר, Panthera pardus pardus
-
מערך של מושיתיים, תרשים של ג.ג. ג'ייקובסן
-
תבנית רבייה של דיונון, Sepia officinalis
היווצרות תבניות[עריכת קוד מקור | עריכה]
אלן טיורינג, ולאחר מכן הביולוג המתמטיקאי ג'יימס ד. מארי, תיארו מנגנון שיצר שאופן ספונטני תבניות של פסים או נקודות: מערכת הפעלה-עיכוב. לתאים של האורגניזם הצעיר יש גנים שעוברים הפעלה באמצעות אות כימי, מורפוגן, כשהתוצאה היא גדילתו של מבנה מסוג מסוים, למשל כתם של פיגמנט כהה על העור. אם המורפוגן נוכח בכל מקום, התוצאה היא צביעה אחידה, כמו במקרה של פנתר שחור. אבל אם הוא לא מפוזר בצורה שווה, התוצאה עשויה להיות פסים או חברבורות. טיורינג הציע כי קיימת בקרת משוב של ייצור המורפוגן עצמו, דבר שיכול ליצור תנודות מתמידות בכמות המורפוגן כאשר הוא מתפזר ברחבי הגוף. יש צורך במנגנון נוסף על מנת ליצור תבניות גל עומד (כדי ליצור פסים או חברבורות): כימיקל מעכב אשר מכבה את ייצור המורפוגן, ושמתפזר בעצמו ברחבי הגוף מהר יותר מהמורפוגן. תגובת בלוסוב-ז'בוטינסקי היא דוגמה לא-ביולוגית של מערכת כזו - מַתְנֵד כימי.
מחקר מאוחר יותר הוביל ליצירת מודלים משכנעים של תבניות מגוונות כמו פסי זברה, כתמי ג'ירפות, חברבורות יגואר (כתמים כהים למחצה המוקפים בטבעות כהות שבורות) ותבניות של מושיות (מערכים גיאמוטריים שונים של נקודות ופסים, ראה איורים). מודלי ההפעלה-עיכוב של ריצ'רד פּרוּם, שפותחו בעקבות עבודתו של טיורינג, משתמשים בשישה משתנים כדי להסביר את הטווח הנצפה של תשע תבניות פיגמנטציה תוך-נוצתיות בסיסיות, מהפשוטה ביותר, כתם פיגמנט מרכזי, וממשיך לכתמים קונצנטריים, פסים, שברונים, "עיניים", צמד נקודות מרכזיות, שורות של זוגות נקודות, ומערך נקודות. מודלים משוכללים יותר מדמים תבניות נוצה מורכבות אצל הפנינייה, שכל אחת מנוצותיה מציגה מעבר מתבנית פסים בקצה הפנימי למערך נקודות בקצה הדיסטלי. תבנית כזו נובעת מתנודה הנגרמת על ידי שני אותות מעכבים, אשר מגיבים זה לזה ברמה הזמנית והמרחבית.
תבניות יכולות להיווצר מסיבות שונות בתבנית הנופית של צמחייה, למשל "שיחי נמר" (tiger bush) או גלי אשוח. פסים של שיחי נמר מתרחשים במדרונות צחיחים שבהם הצמחייה מוגבלת על ידי ירידת גשמים. כל פס אופקי פחות-או-יותר למעשה מנצל את מי הגשם המצויים ישירות מעליו. גלי אשוח נוצרים ביערות על מדרונות הרים לאחר רוחות חזקות, במהלך ההתחדשות של היער. כאשר העצים נופלים, העצים שזכו להגנתם נחשפים, וסביר יותר שהם יינזקו בעצמם, כך שמרווחים כאלו נוטים להתפשט עם כיוון הרוח. בזמן זה, בצד שפונה נגד כיוון הרוח, עצים צעירים צומחים תחת הגנתם של העצים הגבוהים הנותרים. תבניות טבעיות נוצרות לעיתים על ידי בעלי חיים, כמו בתילי המימה (Mima mounds) בצפון-מערב ארצות הברית וכמה אזורים אחרים, שנראה כי נוצרו בעקבות פעילות נבירה מתמדת וארוכת שנים של חולדי השק.[4]
במקרה של קרקעות קפואות-עד בעלות שכבה עליונה פעילה הנוטה לקיפאון והפשרה שנתיים, תבניות עשויות להיווצר באדמה, ביניהן עיגולים, רשתות, מצולעים מטריזי קרח (ice wedges), מדרגות ופסים. התכווצות חום גורמים להיווצרותם של סדקי התכווצות; בזמן הפשרה, מים ממלאים את הסדקים, מתרחבים לקרח כאשר הם קופאים מחדש, ומרחיבים את הסדקים לצורת טריז. הסדקים האלו יכולים להתחבר על מנת ליצור מצולעים וצורות נוספות.[5]
-
כדורנון ("אבו נפחא") ענק, Tetraodon mbu
-
הגדלה של תבנית העור של הכדורנון
-
תצלום מתוך הדמיה של תגובת בלוסוב-ז'בוטינסקי
-
נוצות הפנינייה עוברות ממפוספס למנוקד, הן תוך-נוצתית והן לאורך גוף הציפור
-
מבט אווירי על מישור "שיחי נמר" בניגריה
-
תבניות אדמה: פינגו (pingo) נמס, מוקף במצולעי טריזי קרח, בקרבת טוקטויאטוק (Tuktoyaktuk), קנדה
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Stewart, Ian, What Shape is a Snowflake? Magical Numbers in Nature, Weidenfeld & Nicolson, 2001.
- Ball, Philip, Nature's Patterns: a tapestry in three parts. 1:Shapes. 2:Flow. 3:Branches, Oxford, 2009.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Knott, Ron. "Fibonacci's Rabbits". University of Surrey Faculty of Engineering and Physical Sciences.
- ^ About D'Arcy
- ^ "Spiral Lattices & Parastichy". Smith College. אורכב מ-המקור ב-2010-05-26. נבדק ב-24 בספטמבר 2013.
{{cite web}}: (עזרה) - ^ Morelle, Rebecca. "'Digital gophers' solve Mima mound mystery". BBC News. נבדק ב-9 בדצמבר 2013.
{{cite web}}: (עזרה) - ^ "Permafrost: Patterned Ground". US Army Corps of Engineers. אורכב מ-המקור ב-2015-03-07. נבדק ב-17 בפברואר 2015.
{{cite web}}: (עזרה)