היסטוריה של הפיזיקה עד המאה ה-20
| היסטוריה של הפיזיקה | |
|---|---|
|
פיזיקה היא חקר הטבע, ובמיוחד חקר תופעות הטבע המדידות, כגון תנועתם של כוכבים, דינמיקה של גופים על פני כדור הארץ, תנועת נוזלים, חום, אור וכיוצא באלה.
ההיסטוריה של הפיזיקה היא פירוט התהליכים והאירועים שבהם הועלו השאלות בתחומי הפיזיקה, כיצד התפתחו הכלים להתמודדות עם השאלות הללו - הכלים המחשבתיים והכלים הניסיוניים-טכנולוגיים, וכיצד התפתחו התורות הנותנות מענה לשאלות הללו, תורות המרכיבות את הפיזיקה המוכרת לנו עד למאה ה-20 וכן התורות אשר התגלו כבלתי נכונות ונחשבות עד למאה-20 כמיושנות.
רבות מהשאלות שהעסיקו את הפיזיקאים עד המאה ה-20 הועלו כבר בעת העתיקה, אולם בעת ההיא לא היה הבדל ברור בין דת, מיסטיקה ומדע - והחיפוש אחר תשובות לשאלות הללו הובא במסגרת לימודים דתיים ומיתולוגיות. ביוון העתיקה התפתחה הפילוסופיה השואפת לתת מענה בין השאר גם לשאלות על מבנה החומר והיקום באמצעות טיעונים מבוססי הגיון. התחומים המיוחסים היום לפיזיקה היוו ענף של הפילוסופיה, שנחשבה פילוסופיה טבעית. גדולי המדענים הנחשבים עד המאה ה-20 כפיזיקאים, דוגמת אייזק ניוטון, נחשבו לפילוסופים טבעיים. בימי הביניים, בעיקר בעבודותיו של אבן אל-היית'ם, החלה להתפתח השיטה המדעית, שלפיה יש להכריע בין מודלים שונים של המציאות על סמך ניסוי, גישה שהיוותה בסיס למהפכה המדעית במאה ה-16. בתקופת המהפכה המדעית, החלה הפיזיקה להתגבש כענף נפרד מהפילוסופיה הטבעית. מהפכה זו מסמנת גם את תחילתו של תהליך ממושך של הפרדה בין המדע לבין הדת. המכניקה הניוטונית נחשבת לתחילתה של הפיזיקה הקלאסית, פיזיקה שהגיעה לשיאה במאה ה-19 עם גילוי משוואות מקסוול וחוקי התרמודינמיקה. תחילת המאה ה-20 מסמנת קו גבול חדש, שבו נופצו חוקי הפיזיקה הקלאסית ונולדה הפיזיקה המודרנית.
ההיסטוריה של הפיזיקה קשורה באופן הדוק להתפתחות ענפים מדעיים נוספים, במיוחד המתמטיקה והכימיה. התפתחויות בפיזיקה דחפו ליצירת תורות מתמטיות כגון החשבון האינפיניטסימלי, שהיו חיוניות להתפתחות הפיזיקה. תגליות בכימיה, כהצגת הטבלה המחזורית, היו צעדים חשובים בדרך לגילויים בפיזיקה (במקרה זה לגילוי מבנה האטום ולתורת הקוונטים) שנתנו בסיס מתמטי לכימיה.
התפתחות הפיזיקה הביאה לשינויים משמעותיים בעולם החומרי, במתמטיקה, בפילוסופיה ודרך פיתוח הטכנולוגיה, גם לשינויים חברתיים.
פרהיסטוריה והעת העתיקה[עריכת קוד מקור | עריכה]

בתרבויות קדומות רבות ישנן מיתולוגיות המכילות את סיפור בריאת העולם וכן סיפורים המספקים הסברים לשאלות כגון:
- מדוע עצמים שאינם נתמכים נופלים לארץ?
- מדוע יש לחומרים שונים תכונות שונות?
- מהי צורת כדור הארץ?
- כיצד מתנהגים עצמים שמימיים כמו השמש, הירח והכוכבים, ומדוע?
לדוגמה, במיתולוגיה היוונית תנועת השמש מוסברת בכך שאל השמש (אפולו) נע כל יום בשמים במרכבה עשויה אש, וכן שברקים הם כלי המלחמה של זאוס מלך האלים.
מספר רב של תרבויות קדומות עסקו בתצפיות אסטרונומיות. לחקר הכוכבים הייתה משמעות דתית רחבה בנוסף לחשיבות מעשית בחקלאות ובניווט, למשל. על פי מיקומי הכוכבים יכלו חקלאים לקבוע במדויק את עונות השנה. כך לדוגמה האתר סטונהנג' שבאנגליה שנבנה בין המאה ה-32 למאה ה-21 לפנה"ס, שימש על פי כמה תאוריות לתצפיות אסטרונומיות[1][2], והציר המרכזי שלו בנוי כך שהשמש תזרח דרכו ביום הארוך בשנה. גם הפירמידה הגדולה של גיזה המתוארכת לאמצע האלף השלישי לפנה"ס, וכן הפירמידות של המאיה מעידות על ידע אסטרונומי נרחב של בוניהם. הניצנים של האסטרונומיה המערבית החלו במסופוטמיה. כישוריהם החשבוניים של הבבלים איפשרו להם למדוד את המרחק לירח בדיוק מרשים. בימיו של נבונסר (747–733 לפנה"ס) החל להתבצע תיעוד שיטתי של תנועת הכוכבים, שאיפשר להם לגלות מחזוריות שונות, כגון מחזוריות של 18 שנה בין ליקויי הירח. תיעוד זה שימש את תלמי כאלף שנים מאוחר יותר, בבואו לתת מודל מתמטי לתנועת הכוכבים.
יוון העתיקה[עריכת קוד מקור | עריכה]
"הנס היווני"[עריכת קוד מקור | עריכה]
יוון העתיקה, ערש התרבות המערבית, העלתה תרומות חשובות להתפתחות הפיזיקה במישורים רבים. הפילוסופיה העשירה שהתפתחה ביוון הציעה שפע של תורות והשקפות לגבי מהות העולם ומרכיביו. הפילוסופיה היוונית הייתה הראשונה שדגלה בהסבר נטורליסטי, ובהשקפה שניתן להכריע בין תאוריות שונות על סמך טיעונים מבוססי היגיון.
בעיית השינוי[עריכת קוד מקור | עריכה]
שתי תפיסות עולם מתחרות שלטו בכיפה ביוון העתיקה. תפיסה אחת טענה שהעולם קבוע ובלתי משתנה והשנייה שהעולם בשינוי מתמיד. כך לדוגמה, פרמנידס (520–430 לפנה"ס) טען שהחומר חייב למלא את היקום בצורה אחידה לגמרי ומכאן שלא ייתכן מקום לשינוי ולתנועה. השינויים שאנו רואים הם אשליה. תלמידו זנון הציג שורה של טיעונים מתמטיים שהראו לכאורה ששינוי בלתי אפשרי. לעומתו, הרקליטוס, שלו מיוחס המשפט "אינך יכול לטבול באותו נהר פעמיים", טען שהעולם בשינוי מתמיד. תלמידו דמוקריטוס טען שהיקום בנוי מיחידות בניין יסודיות הקרויות "אטומים", המתחברים ומתנתקים זה מזה בלי הרף.
אפלטון ועולם האידאות[עריכת קוד מקור | עריכה]
אפלטון הציג פילוסופיה מתוחכמת ששילבה מרכיבים מפילוסופיות השינוי ופילוסופיות המצב הקבוע. אפלטון טען שהמציאות הנראית לעין, שבה שינוי אפשרי, היא השתקפות של עולם נעלה יותר ובלתי משתנה הקרוי 'עולם האידאות'. כך, עצם בעולם, כגון שולחן, הוא חיקוי לא מושלם של השולחן הקיים בעולם האידאות.
הפיזיקה של אריסטו[עריכת קוד מקור | עריכה]
 ערך מורחב – הפיזיקה של אריסטו
ערך מורחב – הפיזיקה של אריסטו
אריסטו, תלמידו רב ההשפעה של אפלטון, פיתח תאוריה מתחרה לזו של מורו. במקום רעיון האידאה, אריסטו טען שלעצמים בעולם יש מהויות או פוטנציאלים הטמונים בהם. כוחות אלה נותנים להם את צורתם. כמו כן, הם שולטים על תנועתם. אריסטו סבר שכל הדברים בעולם הם תערובות של ארבעה יסודות: אדמה, מים, אוויר ואש. הרעיון העומד בבסיסה של תורת התנועה של אריסטו הוא שגופים שואפים להגיע למקומם הטבעי – גופים כבדים, העשויים בעיקר מיסודות האדמה והמים, שואפים להגיע לאדמה וגופים קלים, שעיקרם אש ואוויר, שואפים להגיע למעלה.
אצל אריסטו מנוחה ותנועה הן שתי תופעות פיזיקליות שונות לחלוטין, ואי אפשר לראות באחת מהן מקרה פרטי של השנייה. התאוריה שפיתח אריסטו הסבירה בצורה משכנעת מגוון רחב מאוד של תופעות, למשל מדוע נוצה נופלת לאט יותר מאבן. עם זאת, היא התקשתה להסביר התמדה של חפצים בניגוד לכיוון תנועתם הטבעי, למשל התמדה של חץ הנורה למעלה. אריסטו טען כי וואקום אינו אפשרי בטבע, ולכן אוויר ממלא את הוואקום מתחת לחץ ודוחף אותו מעלה. הסבר זה נתפש על ידי ממשיכי דרכו כלא משכנע. התאוריה הפיזיקלית של תנועה ארצית שפיתח עתידה הייתה לשלוט בכיפה, בשינויים קלים, במשך כאלף שנים עד למהפכה המדעית.
התפתחות המתמטיקה והשפעתה על הפיזיקה[עריכת קוד מקור | עריכה]

ביוון העתיקה עברה המתמטיקה התפתחות של ממש. המתמטיקה האינטואיטיבית של ימי קדם, המבוססת על ניסוי וטעייה הפכה לריגורזית. במתמטיקה ובגאומטריה בפרט פותחו סטנדרטים חדשים של הוכחה המבוססים על גזירה לוגית של משפטים מאקסיומות, במקום הסתפקות בהדגמה של נכונות המשפט באמצעים אמפיריים. שיטה זו, שאינה אמפירית, תרמה להתפתחות המתמטיקה ואגב כך להתפתחות הפיזיקה.
היוונים הקדמונים העלו לראשונה את הרעיון שהמתמטיקה יכולה לתאר את המציאות הפיזית, ובכך הניחו את התשתית לפיזיקה כפי שהיא מוכרת כיום. פיתגורס ותלמידיו גילו קשר בין אורכו של מיתר וצליל המופק ממנו, ובהשפעת תגלית זו האמינו שהמציאות כולה ניתנת לביטוי מתמטי ופיתחו תורה מיסטית סביב מושג המספר. השקפה זו נדחתה בימי הביניים, אך שבה ועלתה החל מהמאה ה-16 וניתן לראות את השפעתה על יוהאנס קפלר, שניסה לתאר את המציאות בלשון המתמטיקה, ושילב בעבודותיו רעיונות מיסטיים הקרובים לתורה הפיתגוראית.
ארכימדס, שחי בסירקוזה במאה השלישית לפנה"ס ונחשב לאחד מגדולי המתמטיקאים בכל הזמנים, חקר בין השאר את תורת המנופים, ואת חוקי הציפה (הקרויים על שמו). שיטת המיצוי שפיתח ארכימדס הייתה למעשה הבסיס לחשבון האינפיניטסימלי, תורה שפותחה כעבור 2,000 שנה, והייתה לכלי מרכזי בפיזיקה.
התפתחות האסטרונומיה[עריכת קוד מקור | עריכה]

הישגיהם הנרחבים של היוונים בגאומטריה איפשרו להם לעמת מודלים שונים של היקום עם תצפיות אסטרונומיות. את הבסיס לתוכנית המחקר היוונית באסטרונומיה הניח אפלטון, אשר טען, בצורה שעלתה בקנה אחד עם התצפיות, שהכוכבים הקבועים הם חלק מכדור חיצוני מושלם הנע בתנועה מעגלית אחידה מסביב לארץ. אולם, כמה גרמי שמים (כוכבי לכת) סוטים מתנועה זו ולעיתים נעים לאחור. מושפע מהרעיונות הפיתגוראים על מרכזיות המתמטיקה בעולם, אפלטון ייסד תוכנית מחקר "להציל את התופעות", כלומר להסביר את תנועתם של כוכבי הלכת באמצעות שילוב מעגלים הנעים במהירות אחידה.
אאודקסוס מקנידוס, תלמידו של אפלטון, אשר הקים מצפה כוכבים על גדות הנילוס, הציג מודל של היקום לפיו כוכבי הלכת נעים סביב הארץ על גבי 26 כדורים (spheres) מקוּנָנים (nested) ומסתובבים, שציריהם נטויים ביחס זה לזה. בספרו 'על השמים' (De Caelo), שהפך לטקסט לימוד מרכזי במהלך ימי הביניים פיתח אריסטו (384 לפנה"ס-322 לפנה"ס) את המודל ושכללו לכדי 55 כדורים. אריסטו נתן לכדורים ממשות פיזיקלית, וטען שהם אכן עשויים קריסטל, ואינם רק מכשיר מתמטי.
מודל אחר התבסס לא על כדורים מקוננים אלא על שלושה מכשירים גאומטריים, האפיציקל, הדפרנט והאקואנט. את האפיציקל הציג לראשונה אפולוניוס מפרגה (המאה השלישית לפנה"ס), והוא פותח ושוכלל על ידי היפרכוס מניקאה. ככל שהמודל שוכלל יותר, הוא התאים טוב יותר לתצפיות האסטרונומיות, אך מאידך הוא הפך למסובך יותר. המודל הגיע לשיא שכלולו בעבודותיו של תלמי, שחי באלכסנדריה במאה השנייה לספירה. את עבודותיו האסטרונומיות סיכם תלמי בספר "אלמגסט" (למעשה זהו שמו של התרגום הערבי של הספר), וספר זה הפך לבסיס של האסטרונומיה במשך ימי הביניים ועד לתקופת המהפכה המדעית.
המודלים המקובלים באסטרונומיה היוונית היו מודלים גאוצנטרים, שבהן השמש והכוכבים סובבים סביב הארץ. מודלים אלו הצליחו להסביר את כל התופעות הנצפות פרט לשינוי בעוצמת ההארה של מספר כוכבי לכת במהלך השנה. אריסטכוס בן סאמוס (המאה השלישית לפנה"ס) הציע מודל הליוצנטרי, שבו הארץ סובבת סביב השמש, שיכול להסביר זאת. אולם, מודל זה לא התקבל מארבע סיבות: ראשית, המודל לא היה מפותח מתמטית כמו מתחריו הגאוצנטריים. שנית, לא היה הסבר מדוע הארץ נראית במנוחה, ולמה, אם היא נעה, לא ניתקים ממנה עצמים במעופה. שלישית, אם הארץ משנה את מיקומה ביחס לכוכבים הקבועים, היינו מצפים להבחין בפרלקסה, אולם האסטרונומים היוונים לא הבחינו בתופעה זו (כיום ידוע שהכוכבים הקבועים נמצאים במרחק רב הרבה יותר ממה ששיערו היוונים, ולכן הפרלקסה קטנה מאוד, וניתן להבחין בה רק באמצעות טלסקופים משוכללים). רביעית, הארץ נתפשה כמקום מושבם של האלים והאדם.
אף על פי שבמיתולוגיה היוונית כדור הארץ מתואר כשטוח ואף מתואר כי באחד ממסעותיו הגיע הרקולס עד לקצה העולם, היו מדענים יוונים ששיערו שכדור הארץ הוא עגול. ארטוסתנס, שחי במאה השלישית לפנה"ס, הצליח לקבוע את היקף כדור הארץ על ידי מדידת השינוי באורך הצל במקומות שונים באותה השעה. הערכתו הייתה גדולה בכ-15% מערכו הידוע של ההיקף.
הודו וסין בעת העתיקה ובימי הביניים[עריכת קוד מקור | עריכה]

מגנטיות[עריכת קוד מקור | עריכה]
המצפן הומצא בסין והעדות הכתובה הראשונה לגביו מגיעה מטקסט של שן קואו (Shen Kuo) משנת 1088. קואו (1031–1095), מדען, אסטרונום ואיש אשכולות סיני, ביסס לראשונה את ההבדל בין הקוטב הצפוני הגאוגרפי לקוטב הצפוני המגנטי. נוסף לעבודה זאת, קואו היה מתמטיקאי פורה ופיתח נוסחאות רבות שזכו לשימוש בטריגונומטריה, ובחשבון אינפינטיסמלי. בנוסף הוא ביצע מספר ניסויים באופטיקה, העיר על כך שדמויות מתהפכות כאשר מביטים עליהם דרך מראות קמורות.
אסטרונומיה[עריכת קוד מקור | עריכה]
רישומים של תנועת הכוכבים נעשו בסין החל מהמאה ה-6 לפנה"ס. במאה ה-4 לפנה"ס החל קיטלוג של קבוצות הכוכבים, ובמאה הראשונה לספירה, ז'אנג הנג (78-Zhang Heng 139) קטלג 2,500 כוכבים, ומעל 100 קבוצות כוכבים. במאה ה-13 פעל בסין האסטרונום הגדול גו שוג'ינג (1231–1316). הוא הקים 27 מצפי כוכבים, חישב את אורך השנה כ-365.2425 יום (כלומר רק 26 שניות פחות מהערך המקובל היום) וביסס בשנת 1281 את לוח השנה הסיני.
הטקסט ההודי המוקדם ביותר המוקדש לאסטרונומיה הוא ה"Vedānga Jyotiṣa" שפורסם בסביבות 1200 לפנה"ס. הטקסט מתאר את תנועת הכוכבים לצרכים דתיים ואסטרולוגיים. בעקבות כיבוש הודו על ידי אלכסנדר מוקדון הושפעה האסטרונומיה ההודית מהאסטרונומיה היוונית. במאה ה-5 לספירה פעל המתמטיקאי אסטרונום אריאבהטה (550-476 לסה"נ). אריאבהטה המציא את שיטת הספירה העשרונית (השיטה הנהוגה היום לייצוג מספרים), ותרם תרומות רבות לפיתוח הטריגונומטריה, ולשימוש בטריגונומטריה לצורך תיאור תנועת כוכבי הלכת. הוא גם חקר את ליקויי השמש והירח, וחישב את אורך השנה. במאה ה-6 וה-7 העיר אוג'ן שימשה כמרכז מתמטיקאי ואסטרונומי, אשר גדול מלומדיו היה בראהמגופטה (Brahmagupta; 598–668). בראהמגופטה תרם תרומות רבות לאלגברה ולטריגונומטריה, ובענף האסטרונומיה נתן שיטות לחישוב מיקומי כוכבים וטען שכדור הארץ עגול ונע. בשנת 770 לספירה הוזמן מלומד מאוג'ן לחצר הח'ליף מנצור על מנת ללמד את האסטרונומיה והמתמטיקה ההודית, והוא הביא איתו את כתביו של ברהאמגופטה שתורגמו לערבית.
תור הזהב של האסלאם[עריכת קוד מקור | עריכה]
 ערך מורחב – תור הזהב של האסלאם
ערך מורחב – תור הזהב של האסלאם
לפי האמונה המוסלמית, בשנת 610 לספירה התגלה, לפני מוחמד, במערה ליד מכה, מלאך וציווה עליו 'קרא!". מהתגלות זאת נולדה דת חדשה, האסלאם, והציווי 'קרא!' הפך למצווה הראשונה של הקוראן. במהלך המאות ה-7 וה-8 הקימו חסידיו של מוחמד אימפריה שהייתה גדולה בשטחה מהאימפריה הרומית ואיחדה שטחים ועמים רבים תחת שלטון, שפה, דת וקשרי מסחר משותפים. המוסלמים למדו מהתרבויות שאותן כבשו וכן מהתרבויות איתן באו במגע, כך לדוגמה בקרב טלס (751 לספירה) נשבו שבויים סיניים אשר לימדו את הערבים את אופן ייצור הנייר (אומנות שהומצאה בסין אך נשמרה על ידי הסינים בסוד). במהרה נבנו בפרס ובבגדאד בתי חרושת לייצור נייר שהוזילו בצורה ניכרת את מחיר הספרים. מהודו האסלאם ייבא בין השאר את השיטה העשרונית, ואת מושג האפס ומהאימפריה הביזנטית המוסלמים קנו את ספרי הפילוסופיה והמדע של חכמי יוון העתיקה ורומי. במאה ה-8 היתרגמו ההישגים הצבאיים של האימפריה המוסלמית לשגשוג כלכלי ולפריחה בכל תחומי האומנות והמדע, הקרויה תור הזהב של האסלאם.
את ראשיתו של תור הזהב נהוג לראות בשנת 762, כאשר הח'ליף אל-מנצור מבית עבאס בנה במקום כפר קטן בשם בגדאד את הבירה המפוארת והמשגשגת של האימפריה. הח'ליף אל-מאמון (786–833) בנה בבגדאד את בית החוכמה שהיה ספרייה ומכון תרגום ומחקר. מלומדים מוסלמים תרו את האימפריה בחיפוש אחר כתביהם של מלומדים פרסיים הודים ויוונים, אותם הם תרגמו לערבית והפכו לזמינים לנחלת הכלל. המלומדים לא הסתפקו בתרגום אלא המשיכו את המחקר. המרכז המתחרה לבגדאד מבחינה מחקרית שכן בקורדובה, ובין מרכזי המחקר המרכזיים ניתן לציין גם את קהיר ומרוקו. מלומדים מוסלמים הגיעו להישגים יוצאי דופן ברפואה (ובין הרופאים המפורסמים של התקופה ניתן לציין גם את הרמב"ם שחי בקהיר), כגון המצאת סוגים רבים של ניתוחים, והמצאת האלגברה. בתחום הפיזיקה, המציאו המדענים המוסלמיים את האופטיקה, עשו מחקרים רבים באסטרונומיה, בדינמיקה – וכמו כן נתנו דגש רב ליצירת שיטה מדעית מבוססת ניסוי.
בשנת 1258 בגדאד נכבשה על ידי המונגולים, נבזזה ונשרפה; יש הרואים בשנה זאת את סוף תור הזהב האיסלאמי, ואולם המלומדים והאומנים המוסלמיים המשיכו להנהיג את ההתפתחות התרבותית של העולם עד לשלהי המאה ה-16, כאשר בעקבות הרנסאנס החלה אירופה לקחת את ההובלה.
הולדת האופטיקה[עריכת קוד מקור | עריכה]

האופטיקה בצורתה המודרנית נולדה בעקבות עבודותיהם של מדענים אסלאמיים ביניהם אבן סינא (980–1037), אבו ריהן אל-בירוני (973–1048), קטב אל שירזי (1236 – 1311), קמל אל דין אל פריסי (1260–1320) ומעל כולם מעבודותיו של אבן אל-היית'ם.
אבן אל-היית'ם נחשב למדען הגדול ביותר של התקופה. אל היית'ם ומדענים מוסלמים נוספים היו הראשונים לתת את ההסבר המקובל היום לראייה: שקרני האור יוצאות מהשמש פוגעות בעצמים ולאחר מכן מגיעות לעין (זאת בניגוד להסברים המקובל ביוון העתיקה שהאור יוצא מהעיניים). אל היית'ם הראה שהאור נע בקווים ישרים, ואל בירוני היה הראשון לגלות שמהירות האור גדולה בהרבה ממהירות הקול. אל היית'ם ואבן סינא מדדו את חוקי ההחזרה והשבירה של האור, ואל שירזי יחד עם אל פריסי היו הראשונים לתת את ההסבר הנכון לתופעת הקשת בענן, הסבר המבוסס על חוקי השבירה של האור. אל היית'ם המציא את הקמרה אובסקורה ואת תגליותיו בתחום האור פרסם בספר בשם ספר האופטיקה שנחשב יחד עם הפרינקיפיה של ניוטון לאחד הספרים המשפיעים ביותר בהיסטוריה של הפיזיקה.
אסטרונומיה[עריכת קוד מקור | עריכה]


מדענים אסלאמיים היו הראשונים לבסס את האסטרונומיה כמדע בפני עצמו, הנפרד מהפילוסופיה הטבעית והנפרד מאסטרולוגיה. מבחינה דתית הקוראן מעודד את המוסלמים לחקור את הכוכבים כדי לאפשר להם לנווט טוב יותר, ואכן מדענים אסלאמיים שיכללו מכשירים לצפייה בכוכבים (כגון האצטרולב) לצורכי ניווט ואכן עד היום לרבים מהכוכבים המשמשים לניווט ישנם שמות ערביים. חקר תנועת הכוכבים, ובעיקר חקר תנועת הירח שימשו גם לקביעת ראש החודש (שהוגדר באסלאם כיום ההופעה של ירח בצורת מגל).
מלומדים אסלאמיים תרגמו לערבית את עבודותיהם של אסטרונומים פרסיים, הודיים ויוונים. העבודה החשובה ביותר באסטרונומיה עד לאותה תקופה, עבודתו של תלמי תורגמה לערבית תחת השם 'אלמגסט' (שהפך לשם המקובל לספר זה עד ימינו – מכיוון שהטקסט המקורי אבד), ומלומדים ערבים ניתחו את תצפיותיו ואת מודל האפיציקלים שלו בעזרת הכלים של הטריגונומטריה שפותחו בהודו ושוכללו בארצות ערב, שהפכו את החישובים לפשוטים יותר. בנוסף הוקמו מצפי כוכבים בבגדאד, בדמשק ובמאה ה-13 הוקם מצפה כוכבים חשוב בעיר מראגה שבצפון איראן. בין הגילויים הניסיוניים החשובים היו העדויות הראשונות לסטיות מהמודל של תלמי, שהתגלו על ידי איבן אל שטיר, ועדויות ראשונות לכך שכדור הארץ מסתובב סביב ציר שהתגלו על ידי נסיר א-דין א-טוסי ועלי אל קושג'י מהמצפה במראגה. בזכות תגליות אלו ואחרים התקופה נקראת גם 'מהפכת מראגה', מהפכה שהניחה את היסודות ל'מהפכה הקופרניקאית'.
בצד התאורטי מדענים אסלאמיים נחשבים למייסדים של האסטרופיזיקה, בכך שהם החלו לטעון שהחלל צפוף פחות מהאוויר, החלו להתגלות ממצאים לכך שהכוכבים אינם מוצקים, ושאותם כוחות המאפיינים תנועה על גבי כדור-הארץ מאפיינים גם את תנועת הכוכבים. אל-היית'אם ומדענים ערבים נוספים שיערו את חוק המשיכה בין מסות, שהתגלה מאוחר יותר על ידי גלילאו גליליי ואייזק ניוטון.
התפתחויות בתחומים סמוכים[עריכת קוד מקור | עריכה]
מתמטיקה – אחת התרומות החשובות של המדע הערבי הגיעו מפיתוח ענפים במתמטיקה שלהם הייתה חשיבות רבה בהתפתחות הפיזיקה. מוחמד אבן מוסא אל-ח'ואריזמי (על שמו קרוי המונח אלגוריתם) נחשב למייסד האלגברה, ומקור המילה "אלגברה" היא בכותרת ספרו של אל-ח'ואריזמי "חיסאב אל-ג'אבר ואל-מוקאבלה" ("חשבון ההשלמה וההקבלה"). בנוסף המלומדים הערביים למדו את ספריו של אריאבהטה, מלומד הודי, ומהם למדו את השיטה העשרונית לכתיבת מספרים, וכן את מדע הטריגונומטריה – שאותו הם שיכללו.
אלכימיה – מלומדים ערביים העמיקו בחקר האלכימיה, ענף שבו על ידי ערבוב חומרים שאפו להפוך מתכות פשוטות לזהב, וכן ליצור את אבן החכמים – תרופה שתאפשר חיי נצח. האלכימיה מייסודה כללה שילוב של שיטות מדעיות יחד עם אמונות טפלות ומיסטיקה, אך היא יצקה את הבסיס לכימיה המודרנית. שיטות העבודה והחומרים שהתגלו בעבודותיהם של אלכימאים הפכו לכלים מרכזיים בפיזיקה.
ימי הביניים באירופה[עריכת קוד מקור | עריכה]
התקופה שבין המאה ה-5 למאה ה-16 לספירה קרויה במערב בשם "ימי הביניים", ומציינת את התקופה שבין העת העתיקה והרנסאנס. תקופה זאת באירופה נחשבת כתקופה של קיפאון מדעי, בה הכנסייה שלטה על סדר היום הציבורי והמחקר המדעי הצטמצם לכדי העתקה ולימוד של כתבי הקודש וכתביהם של חכמי יוון העתיקה (בעיקר כתביו של אריסטו). מאידך, בתקופה זו הפכה ההשכלה הציבורית לרווחת יותר, הוקמו האוניברסיטאות הראשונות ויותר מדענים החלו להיות מועסקים באוניברסיטאות ובחצרות של נסיכים ומלכים. כתבים ערביים הכוללים את ה"אלמגסט", את "ספר האופטיקה" של אבן אל-היית'ם ונוספים תורגמו ללטינית, ויחד איתם הגיעו לאירופה תורות כמו האופטיקה, האלכימיה, האלגברה והטריגונומטריה. כמו כן חלו התפתחויות טכנולוגיות רבות הקשורות לשימוש באבק שרפה, בתותחים, במשקפיים ובטכנולוגיות הקשורות לספנות ונווטות ולמעשה נוצקו היסודות שיאפשרו את הפריחה הגדולה שתחל בתקופת הרנסאנס.
תפיסת העולם התאולוגית-קוסמולוגית באירופה של ימי הביניים[עריכת קוד מקור | עריכה]
במאה ה-13 הכניסה הכנסייה הקתולית את הפיזיקה של אריסטו במסגרת השקפתה התאולוגית. התאולוג תומאס אקווינס שילב את התאוריות הקוסמולוגיות האריסטוטליות בתאולוגיה של הכנסייה. בימי הביניים סמכותה האינטלקטואלית של הכנסייה הקתולית הייתה בלתי מעורערת. היא דגלה בהשקפת עולם קוהרנטית וכוללנית, שבה משולבים יסודות פיזיקליים-אריסטוטליים ורעיונות תאולוגיים. היקום האריסטוטלי קיבל מקום ומשמעות החורגים בהרבה מתוכנו הקוסמולוגי. השמים נתפסו כמקום משכנו של האל, מרכז האדמה כמקום משכנו של השטן, והאדם נמצא בתווך – שם מקומו, על פי השקפת הכנסייה, על מהותו של האדם ויכולת הבחירה בין טוב לרע. מהפכה בתחום האסטרונומיה, אם כן, הייתה צריכה להיות בהכרח בעלת השלכות עמוקות גם על התאולוגיה. באותה תקופה שימשו התורות הללו כבסיס האידאולוגי של המשטרים הקיימים. סמכותו של מלך, למשל, נתפסה כנובעת במישרין מרצון האל. ערעור יסודות התאולוגיה היה אפוא בעל משמעות והשלכות מהפכניות חברתיות ופוליטיות.
המהפכה המדעית באירופה (המאה ה-16 וה-17)[עריכת קוד מקור | עריכה]
| |
ראו גם – המהפכה המדעית |

תקופת הרנסאנס, שהחלה באיטליה במאה ה-14, הייתה תקופה של תחייה והתחדשות בכל ענפי התרבות, הרוח והמדע. המהפכה המדעית הייתה בראש ובראשונה מהפכה בשיטת המחקר המדעי: ביסוס המדע על ניסוי ועל תורות מתמטיות. בתחום הפיזיקה, חל שינוי בתפישת העולם; תנועת הכוכבים הוסברה בעזרת מודל לפיו כדור הארץ סובב את השמש ולא ההפך (ראו גם: המודל ההליוצנטרי). עבודותיהם של גלילאו גליליי ואייזק ניוטון ביססו את המכניקה והדינמיקה; נוסדה האופטיקה המודרנית, בעיקר בזכות עבודותיהם של יוהאנס קפלר, ניוטון וכריסטיאן הויגנס; הומצאו המצאות רבות, ביניהן הטלסקופ, המיקרוסקופ ושעון המטוטלת, שלהן תהיה השפעה רבה על התפתחות הפיזיקה; כמו כן, חלו התפתחויות בשאר תחומי המדע – הביולוגיה, הכימיה, האלכימיה ומדעי הרפואה, שלהם תהיינה השפעות עקיפות אך משמעותיות על התפתחות הפיזיקה.
בכל רחבי אירופה, החל מראשית המאה ה-16, היה מפץ של פעילות אינטלקטואלית, כתוצאה ממכבש הדפוס שהכפיל את מספרם ואת המגוון של ספרים בתפוצה כללית. אנשים יכלו כעת ללמוד ממקור ראשון יותר טקסטים מאשר אי פעם. הפרסום מחדש בוונציה של הספרים המקוריים של ארכימדס עורר גל חדש של מחקר מתמטי, ומעתה והלאה עבודותיהם של חוקרים היו נגישות לעמיתיהם בארצות אחרות תוך מספר חודשים. הדפוס יצר שינוי ניכר ביותר ביעילות של התקשורת המדעית. אנשים שגרו במקומות רחוקים זה מזה יכלו מעתה לשתף פעולה. לפני 1500, גם אם הושגו הישגים מדעיים ומתמטיים הם לא הפכו לנחלת הכלל ולכן אבדו, אך החל מ-1550 לערך, החל תהליך של האחדת הידע וחוקר בתחום מסוים בתקופה זו קרא את החומר הישים לעבודתו שפורסם על ידי אחרים, דבר שאפשר לו להמשיך את מחקריו מעמדה עדכנית, ולא מאפס או כמעט מאפס.
ביסוס המדע על ניסוי[עריכת קוד מקור | עריכה]
בימי הביניים באירופה הלימוד המדעי התבסס בעיקר על למידה של כתביהם של הפילוסופים של יוון העתיקה, ובראשותם אריסטו, ועל תיאור ניסויי מחשבה המבוססים על ניסיון יומיומי. מדענים אסלאמיים, ובראשם אבן אל-היית'ם טענו שיש להשתמש בניסויים על מנת לבסס תפיסות מדעיות.
ביסוס המדע על ניסוי הוא אחד הרעיונות המרכזיים שבוססו במהלך המהפכה המדעית. הסמל המפורסם ביותר לשיטה זאת היה גלילאו גליליי. בניסוי מפורסם (אם כי יש טענות שהניסוי מעולם לא התבצע באמת) של השלכת עצמים מהמגדל הנטוי בפיזה, הוא הראה שבנפילה חופשית, גופים בעלי משקלים שונים מגיעים לארץ בו זמנית. ניסוי זה סתר את התאוריה של אריסטו שהייתה מקובלת באותם ימים, לפיה ככל שמסתו של גוף גדולה יותר כך הוא יגיע מהר יותר לקרקע. גליליי תמך בתורתו של קופרניקוס, לפיה כדור הארץ מסתובב סביב השמש ולא להפך, תאוריה שסתרה את עמדת הכנסייה. בשל כך הועלה למשפט, ונגזר עליו מאסר ממושך שלבסוף הומתק למאסר בית. משפט זה מסמל יותר מכל את הקרע שהחל להתהוות בין המדע לבין הדת. אירוע נוסף שהיה חשוב לביסוסה של השיטה המדעית החדשה הוא הופעתם של כוכבים חדשים בשמים בשנים 1540 ו-1604. תופעה זאת, שמוסברת היום על ידי התפוצצות סופרנובות, הייתה בעלות משמעות מיוחדת מכיוון שהיא סתרה את התורה של אריסטו, לפיה הספירה העליונה ביותר של הכוכבים היא מושלמת ולא ייתכנו בה שינויים.
כדור הארץ והשמש[עריכת קוד מקור | עריכה]


את ראשיתה של המהפכה המדעית נהוג לראות בעבודותיו של ניקולאוס קופרניקוס (1473–1543). קופרניקוס נתן מודל לתנועת כוכבי הלכת, לפיו השמש נמצאת במרכזה של מערכת השמש, וכדור הארץ ושאר כוכבי הלכת נעים סביבה במעגלים. מודל זה נקרא "המודל ההליוצנטרי", לעומת המודלים הגאוצנטריים שקבעו שכדור הארץ נמצא במרכז היקום. ספרו של קופרניקוס, "על תנועתם של גרמי השמים" (De revolutionibus orbium coelestium), התפרסם רק לאחר מותו.
המודל ההליוצנטרי שהציע קופרניקוס התבסס על מערכת האפיציקלים שעליה היה מבוססים המודלים הגאוצנטריים, ולמעשה היה מסובך יותר מהם משום שהכיל יותר אפיציקלים. השוני המהותי מהמודלים הגאוצנטריים, בנוסף לכך שהשמש הייתה במרכז ולא הארץ, היה שכוכבי הלכת תמיד במרכזו של מעגל ולא בנקודה אחרת בתוך מעגל, מה שנתפס על ידי קופרניקוס כהנחה לא תקינה.
יוהאנס קפלר (1571–1630) הושפע מקופרניקוס והציע מודל הליוצנטרי משלו. קפלר שנולד והתחנך בגרמניה, התקבל לחצרו של האסטרונום טיכו ברהה בפראג. טיכו היה האסטרונום הגדול ביותר בתקופה שקדמה לטלסקופ. קפלר סבר שמסלולי כוכבי הלכת תואמים את חמש הצורות הגאומטריות המושלמות, אך הוא מעולם לא הצליח ליישב את ההשערה הזאת בדיוק מספיק עם המדידות. משום כך פנה אל טיכו שברשותו היו המדידות המדויקות ביותר של המרחקים אל הכוכבים שהיו בנמצא באותה עת. טיכו קיבל את קפלר בחמימות לחצרו, אך חשש לתת לו גישה אל הנתונים מכיוון שהוא לא האמין במודל ההליוצנטרי (טיכו האמין בתפיסה שהכוכבים נעים סביב השמש, אך השמש נעה סביב כדור-הארץ).
לאחר שרשרת של ויכוחים מרים, קיבל קפלר גישה אל הנתונים שנאספו לגבי התנועה של מאדים. בתחילה הכריז קפלר שהוא יצליח לפענח את הנתונים תוך חודשיים, ואולם המלאכה דרשה ממנו שבע שנים, ולבסוף הביאה אותו למסקנה שמסלוליהם של הכוכבים סביב השמש אינם מעגליים אלא אליפטיים. בכך נפטר קפלר ממערכת האפיציקלים המסובכת. בנוסף, הוא גילה שבתנועתם סביב השמש, הכוכבים מכסים שטחים שווים במרווחי זמן שווים – ומכאן שככל שהכוכבים קרובים יותר לשמש – כך מהירותם גדלה. כמו כן גילה שזמן המחזור של כוכבים יחסי לחזקה של המרחק שלהם מהשמש, ומכאן שככל שמרחקם של כוכבי הלכת מהשמש גדל, כך זמן המחזור שלהם גדול יותר. חוקים אלו ידועים היום בתור שלושת החוקים של קפלר.
הדינמיקה של גלילאו[עריכת קוד מקור | עריכה]
גלילאו גליליי (1564–1642) היה אחד המדענים הראשונים לחקור את הדינמיקה לעומק. הוא גילה, בין השאר, שתנועה של גופים בנפילה חופשית היא פרבולית, וכן שזמן המחזור של מטוטלות אינו תלוי במשרעת (אמפליטודה) שלהן.
בצעירותו ניסה גלילאו לתת ביטוי מתמטי לפיזיקת האימפטוס, שהתפתחה מהפיזיקה של אריסטו. אולם, מושג האימפטוס, שלא התיישב היטב עם הפיזיקה האריסטוטלית, היה מבולבל וקשה לכימות. כדי לתת ביטוי מתמטי לתופעות הטבע, גלילאו ויתר עליו לחלוטין ובנה תחתיו תורה חדשה של תנועת עצמים על פני כדור הארץ, שהחליפה את תורת התנועה של אריסטו. הרעיון העומד בבסיסה של תורת התנועה של אריסטו הוא שגופים שואפים להגיע למקומם הטבעי. לעומת זאת, העיקרון שעומד בבסיסה של תורת התנועה החדשה של גלילאו הוא עיקרון ההתמדה.
עיקרון ההתמדה אומר שגוף נע כלשהו ימשיך בתנועתו כל עוד אין פועלים עליו כוחות חיצוניים. זה ההבדל היסודי בין תורת התנועה של גלילאו לזו של אריסטו: אצל אריסטו תנועה תמיד זקוקה לסיבה, כלומר לכוח מניע. לעומתו טוען גלילאו שתנועה, או לפחות המשך התנועה, אינה זקוקה לסיבה – התנועה נמשכת מאליה כל עוד לא מתערבים בה מבחוץ. מה שזקוק לסיבה הוא שינוי התנועה. הגוף הנזרק מספינה נעה נע יחד איתה לפני זריקתו. לפיכך, נוסף על תנועתו מעלה ומטה בעקבות הזריקה ובהשפעת הכובד, הוא גם ימשיך לנוע קדימה במהירות זהה למהירות הספינה. בסופו של דבר ישוב הגוף וייפול בנקודת הזריקה על הסיפון, ממש כפי שהיה עושה בספינה נחה, ומכאן שאין תוצאות הניסוי יכולות ללמדנו אם הספינה "באמת" נעה או נחה.
באופן דומה אפשר לטעון שגם תוצאות ניסויים של זריקת גופים על פני כדור הארץ אינם מושפעים מתנועתו. לפי אריסטו שינוי זקוק תמיד לסיבה, וההבדל בין תורת התנועה שלו לזו של גלילאו וניוטון הוא בשאלה מהו שינוי. אצל גלילאו וניוטון אין הבדל עקרוני בין מנוחה לבין תנועה בקו ישר ובמהירות קבועה, ולפיכך אפשר לראות מנוחה כתנועה במהירות אפס. אצל אריסטו, לעומת זאת, מנוחה ותנועה הן שתי תופעות פיזיקליות שונות לחלוטין, ולפיכך אי אפשר לראות באחת מהן מקרה פרטי של השנייה. במסגרת תורת התנועה החדשה של גלילאו, אפשר, אפוא, לקבל את השערת קופרניקוס האומרת שהארץ נעה במהירות עצומה, אף על פי שבניסויים שאנו עורכים איננו חשים בתוצאותיה של תנועה זו.
בשנת 1862 החל אסטרונום אנגלי בשם אדמונד היילי (1656–1742), שהיה ידוע בעיקר בזכות גילוי של כוכב השביט הנושא את שמו, להתעניין בחוקי קפלר. הוא ניסה לראות האם ניתן להשתמש ברעיונות של גלילאו על דינמיקה בשביל להסביר את תנועת הכוכבים ואת חוקי קפלר. כאשר הוא נכשל הוא נסע לבקר את ניוטון על מנת לשכנע אותו לחפש הסבר תאורטי לחוקים הללו. לתדהמתו, גילה היילי שניוטון כבר פתר את הבעיה אך לא פרסם את תוצאותיו. היילי מיהר לשכנע את ניוטון לפרסם את עבודותיו ואף מימן את פרסום הספר "עקרונות מתמטיים של פילוסופיית הטבע".
המכניקה הניוטונית[עריכת קוד מקור | עריכה]

בשנה שבה מת גלילאו נולד מי שנחשב ליורשו וגם לאחד הפיזיקאים והמתמטיקאים החשובים ביותר בכל הזמנים: אייזק ניוטון (1643–1727). ניוטון הניח את היסודות לדינמיקה עם שלושת חוקיו הידועים: החוק הראשון טוען שאם על גוף לא פועלים כוחות, הוא ינוע במהירות קבועה הן בגודלה והן בכיוונה (מקרה פרטי הוא מהירות קבועה השווה לאפס, כלומר הגוף נמצא במנוחה מוחלטת); החוק השני קושר את השינוי בתנועה של גוף לכוחות שפועלים עליו (); החוק השלישי קובע כי כוח שגוף אחד מפעיל על השני, יגרור כוח תגובה של הגוף השני השווה בגודלו ומנוגד בכיוונו. ניוטון שיער שכל הגופים מושכים אחד את השני והכוח גדל ככל שהמרחק ביניהם קטן, הידוע כיום ככוח הכבידה (גרביטציה).
בעזרת שלושת חוקיו וחוק הכבידה האוניברסלי, הסביר ניוטון את כל התופעות הניסיוניות אותן גילו גלילאו וקפלר וכן מגוון עצום של תופעות. אבן הכותרת של הישגיו הייתה הפתרון של הבעיה הדו-גופית: ניוטון הצליח להראות שמסלול של כוכב סביב השמש צריך להיות אליפטי, ולהוכיח באופן תאורטי את שלושת החוקים של קפלר. את העבודות האלו הוא פרסם בספר "היסודות המתמטיים של פילוסופיית הטבע".
מתוך חוקי ניוטון נובעים כמה מהמושגים המרכזיים בפיזיקה: שימור התנע, שימור התנע הזוויתי ושימור אנרגיה. מתוך חוקי ניוטון עולה השקפת עולם דטרמיניסטית, שאומנם נוסחה לראשונה רק במאה ה-18, והיא שמתוך ידיעה של המיקומים ושל המהירויות של כל הגופים ברגע נתון, אזי ניתן לנבא את תנועתם החל מרגע זה והלאה, וכמו כן ניתן לחשב מה הייתה תנועתם בעבר.
חוקי ניוטון הפכו לאבן הבסיס של הפיזיקה ב-300 השנים שלאחר מכן, עד היווצרותן של תורת היחסות ומכניקת הקוונטים.
המצאת הטלסקופ[עריכת קוד מקור | עריכה]

 ערך מורחב – טלסקופ
ערך מורחב – טלסקופ
במאה ה-16 הומצא בהולנד הטלסקופ על ידי מדען ששמו אבד עם השנים (לאחר מכן ביקשו לעצמם מדענים ויצרני עדשות אחרים את זכות הראשונים על ההמצאה). גלילאו גליליי שמע על ההמצאה ומיהר לפתח מכשיר כזה בעצמו, ונראה שהיה המדען הראשון שהשתמש בטלסקופ על מנת להביט בכוכבים. המצאה זו הובילה לשרשרת של גילויים חדשים: גלילאו היה הראשון לראות את הירחים של צדק, הטבעות של שבתאי וכתמי השמש. השימוש במכשירים אופטיים על מנת להביט אל השמים שינה את פני האסטרונומיה.
הולדת האופטיקה המודרנית[עריכת קוד מקור | עריכה]
הניסיון לשכלל טלסקופים הביא גם למחקר על אופן פעולתם. את הבסיס לאופטיקה המודרנית נהוג לראות בספרו של קפלר: "Astronomiae Pars Optica" (החלק האופטי של אסטרונומיה). ניוטון הראה באמצעות ניסוי מפורסם עם שתי מנסרות שהאור הלבן למעשה מורכב מכל צבעי הקשת, וכאשר אור נשבר בזכוכית, זווית השבירה שונה לכל צבע. בעקבות כך הוא פיתח טלסקופ המבוסס על החזרה של אור, באמצעות מראות כדוריות (ולא על עדשות השוברות אור).
מהות האור[עריכת קוד מקור | עריכה]
כריסטיאן הויגנס הגה תורה על פיה האור הוא גל, והסביר את השבירה של האור בתנועה של חזית הגל כאשר היא עוברת בין חומרים (תווכים) שונים. לעומתו, ניוטון קידם תורה על פיה האור מורכב מחלקיקים. בעזרת תיאור זה קל יותר להבין את תופעת ההחזרה של האור על ידי מראות (אך קשה יותר להבין את תופעת השבירה). תורתו של ניוטון הפכה למקובלת, עד שב-1801 הוכיח תומאס יאנג בניסוי שני הסדקים שהאור הוא גל. בתחילת המאה ה-20, עם עבודותיו של אלברט איינשטיין והולדת מכניקת הקוונטים, הסתבר שהאור הוא למעשה שילוב של השניים - גל וחלקיק.
צעדים ראשונים בחשמל[עריכת קוד מקור | עריכה]

תופעות אלקטרוסטטיות היו ידועות ליוונים הקדמונים, והם נקראים על שם המילה היוונית לענבר, שכן כאשר משפשפים חומרים בענבר מבחינים בתופעות חשמליות. תופעת המגנטיות מוזכרת כבר בכתבים סיניים המתוארכים למאה ה-4 לפנה"ס, ובעת העתיקה נעשה בתופעה שימוש לצורך בניית מצפנים. המחקרים של ויליאם גילברט מהמאה ה-17, על חשמל ומגנטיות נחשבים למחקרים המעמיקים הראשונים בתופעות אלו. גילברט פרסם את מחקריו בספר: "המגנט ועיניים מגנטיות ועל המגנט העצום כדור הארץ" (De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure) ובו תיאר ניסיונות על מודל של כדור הארץ לו קרא "'טרלה". בין השאר, הוא טען שכדור הארץ מתנהג כמו מגנט ענק וזו הסיבה שמצפנים מצביעים תמיד אל הצפון. הוא גם חקר רבות את תופעת החשמל הסטטי, שאותו ייצר בעזרת אבני ענבר. גילברט טען נחרצות שחשמל ומגנטיות אינם פנים שונות של אותה תופעה, אולם טענה זו הופרכה שנים רבות מאוחר יותר במחקריהם של מייקל פאראדיי וג'יימס קלרק מקסוול על אלקטרומגנטיות.
הידרוסטטיקה[עריכת קוד מקור | עריכה]
רוברט בויל (1627–1691) היה פיזיקאי ואלכימאי אירי הידוע בעיקר בזכות גילוי חוק בויל הקושר את הנפח של גז עם הטמפרטורה והלחץ שלו. חקר גם את תפקידו של האוויר בהתפשטות קול, את ההתרחבות של המים בעת קפיאתם וכן מחקרים על גבישים וחשמל.
בלז פסקל (1623–1662) היה מתמטיקאי ופיזיקאי צרפתי, אשר בנוסף על עבודותיו בתורת ההסתברות, חקר רבות התנהגות של נוזלים ועבודותיו למעשה ייסדו את ענף ההידרודינמיקה. המציא את המנוף ההידראולי והמשאבה ההידראולית. כיום יחידת מידה ללחץ קרויה על שמו. המציא גם את אחת ממכונות החישוב הראשונות.
תגליות חשובות נוספות[עריכת קוד מקור | עריכה]
משאבת הוואקום הומצאה בשנת 1650 על ידי אוטו פון גריקה (1602–1686). הוא גם הראשון שהשתמש בברומטר כדי לבצע מדידות מטאורולוגיות. ניסויים בוואקום עתידים לשחק תפקיד משמעותי בהתפתחות הפיזיקה, ולאפשר את גילויים של האלקטרון, של מבנה הגרעין ושל החלקיקים האלמנטריים. הוואקום עתיד גם לאפשר המצאות טכנולוגיות כגון הנורה החשמלית, הדיודות הראשונות (שהיו מבוססות על שפופרות קתודיות) ואת מסכי הטלוויזיה הראשונים (CRT).

אלסטיות היא תופעה שנחקרה לראשונה לעומק על ידי רוברט הוק (1635–1703). הוא גילה את החוק הנושא את שמו, הקושר את הכוח שמפעיל קפיץ עם אורכו. המציא ושיכלל מכשירים רבים כגון מאזני קפיץ מיקרוסקופיים וכן מכשירים לחיזוי מזג אוויר. ידוע גם בזכות מחקריו בביולוגיה הכוללים את גילוי התאים.
התפתחויות בתחומים סמוכים[עריכת קוד מקור | עריכה]
מתמטיקה[עריכת קוד מקור | עריכה]
במאה ה-17 חלו מספר פריצות דרך משמעותיות במתמטיקה, שלהן הייתה השפעה חשובה גם על התפתחות הפיזיקה.
רנה דקארט (1596–1650) היה אחד הפילוסופים והמתמטיקאים החשובים בכל הזמנים, שהצליח למעשה לאחד את הגאומטריה עם האלגברה בעזרת המצאת מה שנקרא כיום מערכת צירים קרטזית. בכך ייסד את הגאומטריה האנליטית. כהוקרה על עבודתו, מערכת הצירים הסטנדרטיות נקראת על שמו השיטה הקרטזית. הגאומטריה האנליטית בתורה אפשרה את המצאת החשבון האינפיניטסימלי.
כיום מגדירים מהירות כנגזרת של המיקום, ותאוצה מוגדרת כנגזרת של המהירות, כלומר הנגזרת השנייה של המיקום. חוקיו של ניוטון נותנים למעשה את משוואות התנועה של גופים, הקושרות את מיקום הגופים אל הנגזרת השנייה של המיקום, הנקראות משוואות דיפרנציאליות. אולם, המונח "נגזרת" לא היה קיים באותם זמנים, ולא הכלים המתמטיים להתמודד איתו; לכן נוצר צורך לפתח ענף חדש במתמטיקה שיעסוק במונחים אלו: החשבון האינפיניטסימלי. ענף זה אכן פותח על ידי ניוטון, ובמקביל, וככל הנראה באופן בלתי תלוי גם על ידי הגרמני גוטפריד וילהלם לייבניץ (1646 – 1716). במהלך השנים הבאות התפתח ויכוח מר וארסי בין השניים (שהיו חלוקים בנושאים רבים בתחומי המדע, הפילוסופיה והתאולוגיה) לגבי זכות הראשונים על פיתוח התורה, דבר שייצר קרע גדול בין המדענים האנגלים והאירופים במהלך עשרות השנים הבאות, ולמעשה לפגיעה בהתקדמותו של המדע האנגלי.
תורת ההסתברות המודרנית פותחה בעקבות עבודותיהם של פייר דה פרמה, בלז פסקל וכריסטיאן הויגנס. תורת ההסתברות אומנם פותחה כענף מתמטי טהור, אך היא עתידה למלא תפקיד מכריע בהתפתחות הפיזיקה: היא נותנת את הבסיס למכניקה סטטיסטית ולתרמודינמיקה.
המאה ה-18[עריכת קוד מקור | עריכה]
המאה ה-18 נתנה את הבמה לתנועת עידן האורות. תנועה זו כללה אנשי רוח, פילוסופים ומדענים (ביניהם דני דידרו, תומאס ג'פרסון, עמנואל קאנט, ברוך שפינוזה ווולטייר). מבחינה מדעית, סמלה של התקופה היה ייסודה של האנציקלופדיה המודרנית הראשונה בצרפת, שנקראה האנציקלופדיה הגדולה.
במאה ה-18 באירופה המשיכו מדענים גדולים כגון פייר-סימון לפלס וז'וזף לואי לגראנז' את פיתוח החשבון האינפיניטסימלי ואת השלכותיו על הפיזיקה. דניאל ברנולי הניח את היסודות להידרודינמיקה ולאווירודינמיקה. במאה ה-18 התגלו לראשונה גזים אטומיים, החמצן והמימן, ונוסח לראשונה חוק שימור המסה על ידי אנטואן לבואזיה ובמקביל על ידי מיכאיל לומונוסוב.
מכניקה אנליטית[עריכת קוד מקור | עריכה]
מאז עבודותיהם של ניוטון ולייבניץ, התפתחות החשבון האינפיניטסימלי והפיזיקה היו קשורות בקשר חזק זו לזו. בעיות פיזיקליות היו הזרז לפיתוחן של תורות מתמטיות ואלו מצידן הביאו להבנה עמוקה יותר של הפיזיקה. אחד מגדולי מדעני התקופה היה פייר-סימון לפלס (1749–1829), שנחשב ל"ניוטון הצרפתי". בספרו בן חמשת הכרכים "Mécanique Céleste", הפך לפלס את המכניקה הניוטונית מבוססת גאומטריה, למבוססת על חשבון אינפיניטסימלי. על שמו נקראת היום משוואת לפלס שבעזרתה השתמש כדי לתאר את השדה שיוצר כוח הכבידה, וכיום היא המשוואה המרכזית באלקטרוסטטיקה. הנגזרת השנייה המרחבית, קרויה על שמו הלפלסיאן. לפלס ידוע גם בזכות המצאת טרנספורם לפלס שיחד עם טרנספורם פורייה (על שם ז'אן-בטיסט ז'וזף פורייה (1768–1830)) הפכו לכלים מתמטיים חשובים מאוד בפיזיקה. ללפלס היו עבודות רבות נוספות גם באסטרונומיה, בהסתברות ובהידרודינמיקה.

ז'וזף לואי לגראנז' (1736–1813) היה מתמטיקאי ואסטרונום איטלקי. יחד עם לאונרד אוילר הוא פיתח שיטה הנקראת חשבון וריאציות. שיטה זאת משמשת לפתרון בעיות אופטימיזציה. לגראנז' הבין שאת הפיזיקה כולה ניתן לראות כבעיה של אופטימיזציה. לדוגמה, באופטיקה ניתן להבין את חוקי השבירה וההחזרה באופן שהאור בוחר במסלול המהיר ביותר מנקודת ההתחלה אל נקודת הסיום. באופן דומה הצליח לגראנז' להראות שהמסלולים של גופים במכניקה גם הם פותרים בעיה של אופטימיזציה והגודל שאותו הם מנסים לצמצם נקרא כיום על שמו, לגראנז'יאן. בכך ייסד לגראנז' את המכניקה האנליטית. אחד היתרונות של המכניקה האנליטית הוא פתרון בעיות הכוללות אילוצים. את עבודתו המשיך ויליאם רואן המילטון (1805–1865). עם ניסוח מתקדם אף יותר של חוקי המכניקה, שעתידה להיות חשובה מאוד להתפתחות תורת הקוונטים. ללגראנז' היו מחקרים רבים גם בתחומי האסטרונומיה ובתורת המספרים.
מכניקת הזורמים[עריכת קוד מקור | עריכה]

מכניקת הזורמים (fluid dynamics) היא התחום בפיזיקה העוסק בתנועה של גזים ונוזלים. ראשיתה של מכניקת הזורמים נמצאת בעבודותיו של ארכימדס במאה ה-4 לפנה"ס, אשר גילה את חוק הציפה הקרוי על שמו, ובעבודותיהם של המדענים המוסלמים אל בירוני ואל חזני (מאה ה-11 וה-12 לספירה). במאה ה-17 תחום זה זכה להתעניינות מחודשת בזכות עבודותיו של הפיזיקאי האיטלקי אוונג'ליסטה טוריצ'לי (1608–1647).
במאה ה-18 זכתה מכניקת הזורמים לניסוח שלה המוכר היום, בזכות עבודותיהם של לאונרד אוילר ודניאל ברנולי (1700–1782), פיזיקאי ומתמטיקאי הולנדי, שעבד רוב ימיו בשווייץ. ברנולי היה הראשון לקשור את תורת ההסתברות עם הפיזיקה ובכך ליצור ענף חדש בפיזיקה: המכניקה הסטטיסטית (שבתורה עתידה להיות הבסיס לתרמודינמיקה שתפותח רק בסוף המאה). ברנולי השתמש ברעיונות אלו בשביל לתאר את התנועה של נוזלים וגזים, וידוע היום בעיקר בזכות החוק הקרוי על שמו. חוק זה מהווה למעשה את הבסיס לאווירודינמיקה ולהתפתחות מדע התעופה.
לאונרד אוילר (1707-1783) כתב את משוואות התנועה של זורמים, הקרויות היום על שמו. משוואות אלו היוו הכללה של חוקי ניוטון לרצף, והוא ניתח אותם בעזרת הכלים של המכניקה האנליטית.
חוק שימור החומר[עריכת קוד מקור | עריכה]
 ערך מורחב – חוק שימור החומר
ערך מורחב – חוק שימור החומר
בעקבות גילויו של המימן על ידי הנרי קוונדיש (1731–1810), ושל החמצן על ידי ג'וזף פריסטלי (1733–1804), החל אנטואן לבואזיה (1743–1794) לפרק באופן שיטתי חומרים ולאסוף את כל הרכיבים הנוצרים. מחקרים אלו הביאו אותו לבסס את ההרכב הכימי של חומרים שונים, ולנסח את חוק שימור החומר, הגורס שבכל תגובה כימית, המסה היא קבועה וזהה בתחילת התגובה ובסופה. חוק זה נוסח באותה תקופה, במקביל על ידי המדען הרוסי מיכאיל לומונוסוב (1711–1765). מחקרים אלו היוו את הבסיס למדע הכימיה המודרנית, והייתה להם השפעה רבה גם על התפתחות הפיזיקה.
חשמל[עריכת קוד מקור | עריכה]
ניסוי העפיפונים: בנג'מין פרנקלין (1706–1790), מדינאי, איש רוח ומדע אמריקני. הוא ידוע בעיקר כאחת מהדמויות המרכזיות במלחמת העצמאות האמריקנית ואחד ממנסחי חוקת ארצות הברית. פרנקלין היה מדען חוקר בתחום החשמל; הניסוי המפורסם ביותר שלו היה ניסוי העפיפונים שבו הוא הצליח להראות שברקים הם למעשה התפרקויות של זרם חשמלי.
מנועי הקיטור והמהפכה התעשייתית[עריכת קוד מקור | עריכה]
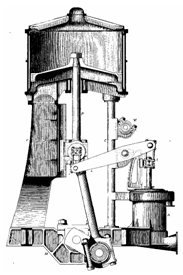
כבר במאה הראשונה לספירה, הומצאה המכונה הראשונה המונעת בידי קיטור. מכונה זאת נקראה כדור איאולוס ופותחה על ידי הרון מאלכסנדריה. היא כללה כדור מלא במים, שממנו יוצאים צינורות. כאשר מחממים את הכדור מלמטה, הקיטור הנפלט ממנו גורם לכדור להסתובב. במאה ה-17 המציא אוטו פון גריקה את משאבת הוואקום הראשונה, ובהתבסס על תכנוניו יצרו רוברט הוק ורוברט בויל את משאבת האוויר הראשונה. המצאות אלו הובילו בתורם לגילוי חוק הגזים האידיאלים, וכן להמצאתם של מנועי הקיטור.
מנוע הקיטור הראשון, שהושפע מרעיונות של דני פפן, נבנה בשנת 1697 על ידי תומאס סייוורי. תומאס ניוקומן שכלל את המנוע בשנת 1712 עם המצאת המנוע האטמוספירי. מנועים אלו זכו לשימושים מסחריים, בעיקר לשאיבת מים ממכרות פחם. מי שקידם את מנועי הקיטור יותר מכל היה ג'יימס ואט (1736 – 1819). ואט החל את דרכו המדעית כאשר התאפשר לו להקים בית מלאכה קטן באוניברסיטת גלאזגו. לאוניברסיטה היה דגם של מכונת הקיטור של ניוקומן, ואט שכלל אותו והמכונה הייתה הראשונה שהפכה את מכונות הקיטור לכלכליות ושימושיות למגוון רחב של יישומים. יחידת המידה להספק נקראת על שמו. מכונות הקיטור של ואט וממשיכיו זכו במהרה למגוון עצום של יישומים, בעיקר לשאיבת מים, להנעת אמצעי תחבורה (רכבות ואוניות) ולהנעת מכונות לייצור טקסטיל. המצאות אלו חוללו את המהפכה התעשייתית שלה הייתה השפעה עצומה על התפתחות החברה והכלכלה וכן על התפתחות המדע. המדע נתן את הכלים לפיתוח מכונות יעילות יותר, ומצד שני נהנה מהתוצרים שלהם.
על אף שהמכונות של ואט כבר הפכו לכלכליות, היעילות שלהן הייתה נמוכה: הן ניצלו רק כ-2 אחוז מהאנרגיה שהושקעה בהן. בד בבד עם הניסיונות לשכלל את מכונות הקיטור, החלה לעלות שאלת היעילות המקסימלית שמכונות יכולות להפיק. השאלה הזאת הטרידה בין השאר את מנוחתו של סאדי קרנו (1796–1832), אז מהנדס צבאי בשירותו של נפוליאון בונפרטה. עבודתו התאורטית "הרהורים על כוחה המניע של האש", שהתפרסמה בשנת 1824, הובילה לייסודו של ענף חדש בפיזיקה: התרמודינמיקה.
על מנת להסביר תופעות כימיות כמו התלקחות ופיזיקליות כמו החום, נפוצו במאה ה-17 תאוריות הפלוגיסטון והקלוריק שנחשבות היום למיושנות. על פי תאוריית הפלוגיסטון, שפורסמה לראשונה על ידי יואכים בכר בשנת 1667, בנוסף לארבעת היסודות של החומר (מים, אש, אוויר ואדמה – זוהי תורה שמקורה ביוון העתיקה ועדיין הייתה מקובלת על חלק מהקהילה המדעית במאה ה-18) ישנו גם יסוד חמישי הקשור לבעירה, הקיים בגופים היכולים להתלקח. אנטואן לבואזייה (הנחשב לאבי הכימיה) הפריך את תאוריית הפלוגיסטון (כמו גם את תאוריית ארבעת היסודות) בכך שהראה שבעירה נובעת כתוצאה מתגובות כימיות הקשורות בחמצן. במקום הוא הציג את תאוריית הקלוריק הקובעת שישנו מעין נוזל בשם זה, האחראי על תופעת החום, אשר נוזל בין גופים חמים לקרים. תאוריה זאת הפכה למקובלת על רוב הקהילה המדעית ושימשה כבסיס לעבודותיו של קרנו.
המאה ה-19[עריכת קוד מקור | עריכה]
התרמודינמיקה והמכניקה הסטטיסטית[עריכת קוד מקור | עריכה]
כאמור המהנדס הצרפתי סאדי קרנו ניסה לתת הסבר כללי למהי הנצילות המרבית שניתן להפיק ממנועי קיטור. לשם כך הוא הגה מכונת קיטור אידיאלית, הקרויה על שמו מנוע קרנו, וחישב את היעילות שלה. לאחר מכן הוא הצליח להראות, באמצעות הסתמכות על ההפיכות של המכונה ועל אי ההיתכנות של מכונת תנועה נצחית (פרפטאום מובילה), שלא תיתכן מכונה יעילה יותר. קרנו עבד במסגרת תורת הקלוריק שראתה בחום ישות חומרית דמוית נוזל הזורמת מגוף חם לגוף קר.
המילה תרמודינמיקה מקורה במחקריו של ויליאם תומסון (לורד קלוין) (1824–1907) על נצילותם של מנועי קיטור. תומפסון, בנואה פאול אמיל קלפרון (1799–1864) ורודולף קלאוזיוס (1822–1888) קראו תיגר על תורת הקלוריק והציגו את המושגים אנרגיה, אנטלפיה ואנטרופיה. כמו כן, הם הציגו את החוק השני של התרמודינמיקה הקובע שבמערכת סגורה האנטרופיה תמיד תגדל. בשנת 1798 הדגים בנג'מין תומפסון המרת עבודה מכנית לחום, ובשנת 1847 ניסח ג'יימס ג'ול את חוק שימור האנרגיה, בצורת חום ובצורת אנרגיה מכנית. בכך נוסד ענף התרמודינמיקה המודרנית.
קלאוזיוס יחד עם ג'יימס מקסוול פיתחו תורה המסבירה את התנהגותם של גזים, על פי ההנחה שהגז מורכב ממספר רב של חלקיקים הנמצאים בשיווי משקל. בעשותם כך הם נתנו הסבר לחוקי התרמודינמיקה המבוסס על תורת ההסתברות. לודוויג בולצמן ביסס במקביל אליהם תאוריה דומה ולכן התפלגות המהירויות של אטומים בגז קרויה היום התפלגות מקסוול בולצמן. עבודות אלו יחד עם עבודותיהם של ויליאם גיבס ואמדאו אבוגדרו יצרו את הבסיס של המכניקה הסטטיסטית.
ויליאם תומסון אחראי לאחת מפריצות הדרך המחשבתיות החשובות בהיסטוריה של הפיזיקה בכך שהוא השתמש בתרמודינמיקה בשביל לחקור את השמש. תומסון טען שמכיוון שהשמש פולטת קרינה אזי היא מתקררת. מתוך עוצמת הקרינה של השמש, כפי שהיא נמדדת בכדור הארץ, חישב תומסון את קצב הקרור של השמש והגיע למסקנה שהטמפרטורה של פני השמש לפני 30 אלף שנים הייתה גדולה משמעותית מהטמפרטורה הנוכחית שלה. אומדן זה עמד בסתירה לממצאים גאולוגיים המעריכים את גיל כדור הארץ במאות מיליוני שנה, וכן להערכה של צ'ארלס דרווין המבוססת על תורת האבולוציה לפיה לקח לחיים מיליוני שנים להתפתח. הטעות של תומסון הייתה בכך שלשמש יש מנגנון חימום פנימי, המבוסס על תגובות גרעיניות, ולכן קצב הקירור של השמש קטן בהרבה. מאידך עבודה זאת יצרה את הבסיס שממנו התפתחה האסטרופיזיקה המודרנית.
אלקטרודינמיקה[עריכת קוד מקור | עריכה]

סוף המאה ה-18 והמאה ה-19 ראו את הולדת וההתפתחות המהירה של תורת החשמל והמגנטיות. את הכוח החשמלי הקושר שני גופים גילה שארל-אוגוסטן דה קולון (1736–1806), בשנת 1784. בשנת 1800 המציא אלסנדרו וולטה (1745–1827), פיזיקאי איטלקי, את הסוללה החשמלית, וזאת איפשרה מעתה לבצע ניסויים מעמיקים בחשמל. מעבר לחשיבות היישומית הרבה שלה, הסוללה גם הראתה כיצד ניתן להפוך אנרגיה כימית לאנרגיה חשמלית, ומעתה הגילגולים השונים של אנרגיה חשמלית, הקשרים בין חשמל למגנטיות, לחום, ולאפקטים כימיים ולאור ימשיכו לרתק את העולם המדעי. את המונחים מתח, זרם והתנגדות ניסח גאורג אוהם (1789–1854), שעל שמו קרוי היום חוק אוהם. הנס כריסטיאן ארסטד (1777–1851) היה הראשון להבחין בקשר בין חשמל למגנטיות. ארסטד הבחין שכאשר הוא מעביר זרם בקרבת מגנט, הזרם גורם למחט של המגנט לסטות הצידה.
פריצות הדרך המשמעותיות ביותר בתחום באו בעקבות עבודותיו של המדען האנגלי מייקל פאראדיי (1791–1867). חסר השכלה גבוהה רשמית בתחום, החל פאראדיי להתעניין בחשמל לאחר ששמע על הניסויים של ארסטד הקושרים חשמל עם מגנטיות. הוא גילה בצורה אמפירית כי זרם חשמלי יוצר סביבו שדות מגנטיים. פאראדיי היה אחד המדענים הראשונים שהשתמש ברעיון של שדות על מנת לתאר את חוקי החשמל. הוא המציא את המנוע החשמלי הראשון, וניסח את חוק ההשראה הנושא את שמו.

ג'יימס קלרק מקסוול (1831–1879) החל את דרכו כתלמיד של פאראדיי. מקסוול היה מצויד בהשכלה מתמטית אקדמית טובה יותר מזאת של מורהו, וזאת איפשרה לו לנסח את חוקי החשמל שגילו פאראדיי ואחרים בעזרת ארבע משוואות דיפרנציאליות, אשר נושאות את שמו, משוואות מקסוול. התוצאה המפתיעה ביותר של המשוואות היא המסקנה כי שדה חשמלי משתנה יוצר שדה מגנטי, ומכיוון ששדה מגנטי משתנה יוצר שדה חשמלי, אזי ישנו פתרון למשוואות בצורה של גל אלקטרומגנטי, הנע במהירות האור. מכאן הסיק מקסוול שלמעשה האור הוא גל אלקטרומגנטי. הישג זה היה התגלית המדעית הגדולה של התקופה: איחוד של כל חוקי החשמל, המגנטיות והאופטיקה לתוך ארבע משוואות. התורה של מקסוול זכתה לאישוש ניסיוני עם המצאת הרדיו ב-1888 על ידי היינריך רודולף הרץ (1857–1894), וגילוי קרני ה-X על ידי וילהלם רנטגן (1845–1923) ב-1895.
לתגליות בתחום האלקטרודינמיקה הייתה השפעה עצומה על ההתפתחויות הטכנולוגיות, שהביאו לשינוי פניה של החברה, עם המצאות כגון המנוע החשמלי, הנורה החשמלית, הרדיו, הפטיפון ועוד.
המכניקה ההמילטונית[עריכת קוד מקור | עריכה]
המכניקה ההמילטונית פותחה על ידי סר ויליאם רואן המילטון (1805–1865), מתמטיקאי ואסטרונום אירי. הוא המשיך את עבודותיו של לגראנז' בתחום המכניקה האנליטית והראה שניתן לנסח את חוקי המכניקה בדרך נוספת, על בסיס מה שקרוי היום משוואות המילטון, הנגזרות ממושג ההמילטוניאן שהכניס לשימוש. המשוואות היוו ניסוח מתמטי שונה בלבד, ולא הוסיפו שום דבר מהותי לגבי הבעיות שלפתרונן שמשו. עם זאת, תפקידן ההיסטורי היה מכריע, שכן שפכו אור חדש לגבי הדרך בה ניתן להכליל את המכניקה הקלאסית, ובכך ניתן לראות גם את משוואות המילטון בתור הקו המקשר מהמכניקה הקלאסית אל מכניקת הקוונטים המאוחרת יותר.
החיפוש אחר האתר[עריכת קוד מקור | עריכה]
ניסוי שני הסדקים ב-1801 הראה מעל לכל ספק שהאור הוא גל. נותרה השאלה מהו התווך שנושא את האור, באותו אופן שתווך (למשל, האוויר) נושא את גלי הקול. התווך הזה זכה לשם אתר ונעשה מאמצים רבים על מנת למדוד תנועה של גופים יחסית לתווך זה. הניסוי המפורסם ביותר היה ניסוי מייקלסון-מורלי. הרעיון של הניסוי התבסס על ההנחה שרווחה באותם זמנים, לפיה כדור הארץ נע ביחס לאתר. על סמך תנועה יחסית זו, כך חשבו, ניתן יהיה למדוד את ההבדלים בין מהירות האור בכיוון תנועתו של כדור-הארץ לבין מהירותו בכיוון הניצב. הניסוי לא הצליח למדוד כל הבדל ביניהם. ניסיונות נוספים התבססו על תצפיות אסטרונומיות של הירחים של צדק וגם הם לא הצליחו להבחין בקיומו של האתר.
גאומטריות לא אוקלידיות[עריכת קוד מקור | עריכה]
עד המאה ה-19 רווחה האמונה שהגאומטריה מייצגת תיאור של העולם ואמת בסיסית שאין אחרת לה. רבים ראו פגם אחד מרכזי בגאומטריה, והוא האקסיומה החמישית של אוקלידס, אקסיומת המקבילים, שנראתה מסורבלת ולא הכרחית. בתחילת המאה ה-19, שורה של מתמטיקאים החלו לבנות בנפרד ובאופן בלתי תלוי גאומטריות שבהן האקסיומה הזאת איננה מתקיימת; כלומר, גאומטריות שבהן דרך נקודה שלא על קו נתון, או שלא ניתן להעביר כלל מקבילים לקו, או שניתן להעביר קווים מקבילים רבים לקו הנתון. תורות אלו נקראות היום גאומטריה לא-אוקלידית. ככל הנראה, הראשון שפיתח גאומטריות אלו היה קרל פרידריך גאוס, מגדולי המתמטיקאים בכל הזמנים, ובמקביל לו פיתחו את הגאומטריות הללו גם המתמטיקאי הרוסי ניקולאי איוונוביץ' לובצ'בסקי וקצין הצבא ההונגרי יאנוש בויאי. את אחת התרומות החשובות ביותר לנושא הניח תלמיד של גאוס, ברנהרד רימן. תורות אלו שינו לגמרי את תפיסת המחשבה בקשר למהות של תורות מתמטיות, והייתה להן השפעה חשובה על התפתחות הפיזיקה. תורות אלו עתידות לשחק תפקיד מרכזי בתורת היחסות הכללית. השאלה האם היקום הוא שטוח שמתנהג על פי חוקי אוקלידס ממשיכה להעסיק קוסמולוגים עד ימינו.
קרניים קתודיות וגילוי האלקטרון[עריכת קוד מקור | עריכה]
 ערך מורחב – שפופרת קתודית
ערך מורחב – שפופרת קתודית
כאשר מופעל מפל מתח גדול בין שתי אלקטרודות סמוכות נוצרת פריצה חשמלית ביניהן, תופעה הנראית דומה לברק (למעשה ברק הוא פריצה בין עננים הצוברים מתח רב יחסית לאדמה). כבר במאה ה-18 היו תצפיות לפיהן הסתבר כי ככל שהאוויר דליל יותר, כך מתח יכול לפרוץ מרחקים גדולים יותר. בשנת 1838 הבחין לראשונה מייקל פאראדיי בתופעה של קרניים קתודיות: פאראדיי הרכיב שפופרת זכוכית, אשר בכל קצה שלה ישנה אלקטרודה. כאשר העביר זרם בין האלקטרודות (הנקראות אנודה וקתודה) הוא הבחין שנוצרת קרן אור המתחילה באנודה, עוברת דרך הריק, ומגיעה עד הקתודה. כיום ידוע שהקרן נוצרת מכך שאלקטרונים נפלטים על ידי הקתודה, מואצים ומגיעים לבסוף אל האנודה, ובדרכם מתנגשים בגז המועט שנותר בשפופרת ומעוררים את האטומים, ואלו פולטים קרינה. ג'יי ג'יי תומסון הצליח להראות שהוא מסוגל להטות את הקרניים בעזרת שדות חשמליים, וגם בעזרת שדות מגנטיים. מתוך מדידת הטיות אלו, הצליח תומפסון למדוד את היחס בין מטען החלקיקים בקרניים הקתודיות לבין המסה שלהם. תומפסון גילה שהקבוע שהתקבל קטן מאוד (מרמז על חלקיק מאוד קטן), ואוניברסלי: כלומר, איננו תלוי בתנאים ניסיוניים כמו הרכב הגז בשפופרת, הרכב האלקטרודות וכדומה. תומפסון הסיק את קיומו של חלקיק בסיסי בטבע, האלקטרון.
שפופרות קתודיות זכו למגוון גדול של שימושים. התופעה הבסיסית משמשת עד היום בנורות פלואורסצנטיות. שפופרות קתודיות עומדות בבסיסם של מסכי טלוויזיה מסוג CRT (מסכי הטלוויזיה המקוריים), ושל שפופרות הריק הראשונות. בנוסף, ניסויים בשפופרות קתודיות הביאו לגילוי האפקט הפוטואלקטרי.
התורה האטומית[עריכת קוד מקור | עריכה]
 ערך מורחב – התורה האטומית
ערך מורחב – התורה האטומית
בתחילת המאה ה-19 החל ג'ון דלטון לבסס את התורה האטומית, שלפיה כל החומרים עשויים מאבני יסוד אטומיות, להן משקלים שונים. דלטון החל למדוד ולסווג את היסודות על פי משקליהם כאשר המימן הוא היסוד הקל ביותר. בעקבות עבודותיו של דלטון ושל אחרים התגלו במהלך המאה ה-19 יסודות חדשים רבים ותכונותיהם נחקרו לעומק.
באמצע המאה ה-19, הכימאי הרוסי דמיטרי מנדלייב החל לכתוב ספר כימיה; לצורך הכתיבה הוא ניסה לעשות סדר במגוון העצום של הידע שנצבר. מנדלייב החל לסדר את היסודות הידועים על פי המשקלים האטומיים שלהם מצד אחד, ומצד שני לארגן אותם בטורים לפי תכונות משותפות. בסופו של דבר נוצרה הטבלה המחזורית, לה תהיה השפעה אדירה על התפתחות הכימיה והפיזיקה.
תגליות חשובות נוספות[עריכת קוד מקור | עריכה]
- אפקט דופלר – בשנת 1842 ניסח לראשונה המתמטיקאי האוסטרי כריסטיאן אנדראס דופלר את אפקט דופלר, שלפיו התדירות של גל תלויה במהירות היחסית שבין מקור הגל לבין הצופה. דופלר ניסח את החוק עבור גלי קול, אך החוק נכון למגוון רחב של גלים, ובפרט אפקט דופלר האופטי שלו היה תפקיד חשוב בהתפתחות הפיזיקה. אדווין האבל השתמש באפקט זה על מנת למדוד את המהירות של גלקסיות יחסית לגלקסיה שלנו שהובילה אותו לחוק האבל. באפקט דופלר נעשה שימוש בקירור של אטומים על ידי לייזר, וכן במדידות המדויקות ביותר של תורת היחסות.
- מכניקת הזורמים - הפיזיקאים קלוד לואי מארי נווייה וגבריאל סטוקס חקרו את השפעת הצמיגות על תנועת הנוזלים, וניסחו את משוואת נווייה-סטוקס הקרויה על שמם. הפיזיקאי אוסבורן ריינולדס הראה שישנם שני סוגים של זרימה - זרימה למינרית (זרימה חלקה), וזרימה טורבולנטית. הוא הראה שהמעבר בין סוגי הזרימה נקבע לפי מנה של גדלים פיזיקליים הקרויה היום על שמו: מספר ריינולדס.
סוף המאה ה-19: סוף הפיזיקה?[עריכת קוד מקור | עריכה]
בסופה של המאה ה-19 בזכות הגילויים הגדולים של חוקי התרמודינמיקה, ובעיקר בזכות גילוי חוקי מקסוול, רווחה בקרב הפיזיקאים האמונה שלמעשה התגלו כבר כל החוקים הבסיסיים של הטבע, וכל מה שנותר לפיזיקאים לעשות למעשה הוא להבין את המשמעות של החוקים האלו עבור מקרים פרטיים.
אלא שהיו פיזיקאים שהיו מודעים לכך שהמלאכה לא לגמרי שלמה. בהרצאה מפורסמת בשנת 1900 טען לורד קלווין (ויליאם תומסון) כי ישנם שני עננים המעיבים על השמים היפים של הפיזיקה של המאה ה-19: ניסוי מייקלסון-מורלי (הבעיות במדידת תכונותיו של האתר), וכן הקושי להבין את תופעת קרינת הגוף השחור. הוא אמנם צפה את הבעיות אך המעיט כנראה בערכן משום שבאותה הרצאה אף טען כי "אין שום דבר חדש לגלות בפיזיקה כעת, כל הנותר הוא לבצע מדידות מדויקות יותר ויותר" ואף כי "קרני רנטגן הן תרמית". מה"ענן" הראשון שציין לורד קלווין נולדה תורת היחסות, ומה"ענן" השני נולדה מכניקת הקוונטים. שתי תאוריות אלו עתידות לשנות את הדרך שבה האדם מבין את העולם. בנוסף על כך, גילוי האלקטרון, הרדיואקטיביות ומבנה האטום תרמו לביסוסם של ענפים חדשים בפיזיקה: פיזיקה גרעינית ופיזיקה של חלקיקים אלמנטריים.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
מקורות ראשוניים בהיסטוריה של הפיזיקה[עריכת קוד מקור | עריכה]
- אלמגסט / תלמי (המאה ה-2 לספירה). הגרסה הערוכה על ידי יוהאן לודוויג הייברג לספרו של תלמי ניתנת להורדה כאן.
- ספר האופטיקה / אבן אל-היית'ם (המאה ה-11 לספירה)
- שיחות על שני ענפי מדע חדשים / גלילאו גליליי (1638). גרסה מקורית באיטלקית ניתנת להורדה כאן, ותרגום אנגלי כאן.
- עקרונות מתמטיים של פילוסופיית הטבע / אייזק ניוטון (1687). גרסה מלאה מתוך גוגל ספרים.
מקורות משניים פופולריים בהיסטוריה של הפיזיקה[עריכת קוד מקור | עריכה]
- טימותי פריס, מילדות לבגרות בשביל החלב, ספרית מעריב, תל אביב, 1991.
- טימותי פריס, היקום וכל אשר בו, הוצאת הד ארצי, אור יהודה, 2000.
- Great Physicists - William H. Cropper
- Subatomic Paricles - Steven Weinberg
מקורות משניים אקדמיים בהיסטוריה של הפיזיקה[עריכת קוד מקור | עריכה]
- יואב בן דב. 1991. פיזיקה: תורות ומושגים. ת"א: משרד הביטחון, ההוצאה לאור. (הטקסט המלא זמין באינטרנט כאן).
- Bernard I. Cohen. 1985. The Birth of a New Physics. New York: Norton.
- Gerald J. Holton & Stephen G. Brush. Physics, the Human Adventure: From Copernicus to Einstein and Beyond. New Brunswick, N.J.: Rutgers University Press.
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ נירה ניסקי, סטונהנג': סוד האבנים השואבות, באתר ynet, 21 ביוני 2006
- ^ חוגגים את היום, באתר הארץ, 21 ביוני 2005
| תחומים בפיזיקה | ||
|---|---|---|
| פיזיקה קלאסית | אופטיקה • אלקטרומגנטיות • אסטרונומיה • אקוסטיקה • מכניקה (מכניקה קלאסית • מכניקת הזורמים • מכניקת הרצף) • תרמודינמיקה | |
| פיזיקה מודרנית | אלקטרואופטיקה • אסטרופיזיקה • פיזיקת חלקיקים • פיזיקה גרעינית • פיזיקת מצב מעובה • פיזיקה סטטיסטית • תורת היחסות (הכללית • הפרטית) • מכניקת הקוונטים • תורת השדות הקוונטית • תורת המיתרים • פיזיקה כימית | |
| נושאים בינתחומיים | ביופיזיקה • פיזיקה רפואית • גאופיזיקה • פיזיקה מולקולרית | |
| היסטוריה של הפיזיקה | היסטוריה של הפיזיקה עד המאה ה-20 • התפתחות הפיזיקה במאה ה-20 | |



