טרפז שווה-שוקיים

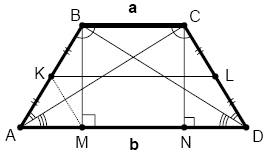
טרפז שווה-שוקיים

טרפז שווה־שוקיים הוא טרפז שהשוקיים שלו שוות זו לזו באורכן (AB=CD). הגדרה שקולה היא טרפז שזוויות הבסיס שלו שוות זו לזו.

על-פי ההגדרה המרחיבה, ניתן לראות במקבילית סוג של טרפז. ואז מתקיים כי מקבילית שהיא גם טרפז שווה-שוקיים היא בהכרח מלבן. וכל מלבן הוא טרפז שווה-שוקיים.

כמו בכל טרפז, השטח של טרפז שווה־שוקיים שווה לממוצע חשבוני של אורך הבסיסים כפול הגובה.

תכונות של טרפז שווה־שוקיים

ציר הסימטריה של טרפז שווה-שוקיים

• זוויות הבסיס שוות זו לזו (בטרפז יש שני זוגות של זוויות בסיס, ואם הזוויות שוות בזוג אחד, הן שוות גם בזוג השני).
• זוויות נגדיות משלימות ל-180 מעלות.
• הגובה העובר דרך מפגש האלכסונים הוא ציר סימטריה של הטרפז שווה השוקיים. לפיכך, הגובה העובר דרך מפגש האלכסונים - חוצה את הבסיסים.
• אלכסוני הטרפז שווה-השוקיים שווים זה לזה (AC = BD).
• האלכסונים יוצרים עם הבסיסים משולשים שווי-שוקיים ($\ AO=DO$, $\ CO=BO$) ועם השוקיים שני משולשים חופפים.
• היחס בין החלקים של האלכסונים שווה ליחס בין הבסיסים: ${\frac {AO}{CO}}={\frac {DO}{BO}}={\frac {AD}{BC}}$ (משפט תאלס).
• נסמן ב-$a=BC$ וב-$b=AD$ את ארכי הבסיסים, וב-$c=AB=CD$ את אורך השוק. אורך האלכסונים הוא ${\sqrt {ab+c^{2}}}$ (תוצאה של משפט פיתגורס במשולשים BDM ו-ABM).
• כל טרפז שווה-שוקיים הוא מרובע ציקלי, כלומר מרובע שניתן לחסום אותו במעגל.
• כל טרפז שניתן לחסום אותו במעגל הוא שווה-שוקיים.

טרפזים שווי-שוקיים מיוחדים

• טרפז שווה-שוקיים חוסם מעגל אם ורק אם השוק שווה לקטע האמצעים.
• בטרפז שווה-שוקיים שבו האלכסונים ניצבים זה לזה, הגובה שווה לקטע האמצעים, והשטח שווה $h^{2}$. הסיבה לכך היא שהבסיסים יוצרים עם האלכסונים שני משולשים שווי-שוקיים וישרי זווית - בהם הגובה הוא תיכון ליתר (בסיס), ולכן שווה למחצית היתר. לכן גובה הטרפז שווה למחצית סכום הבסיסים.
• בטרפז שווה-שוקיים שבו אחד הבסיסים שווה לשוק, האלכסונים חוצים את זוויות הבסיס השני.

קישורים חיצוניים

• טרפז שווה-שוקיים, באתר MathWorld (באנגלית)