ארבעון
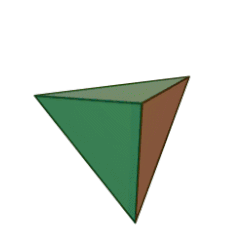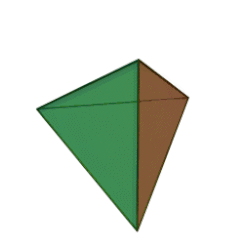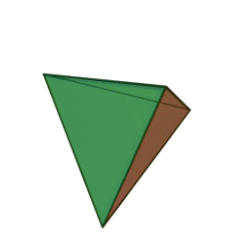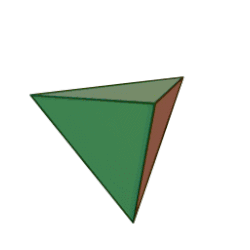


אַרְבָּעוֹן[1] (גם טטראדר או טטרהדרון; באנגלית: Tetrahedron) הוא פירמידה משולשת, כלומר גוף שכל ארבע פאותיו הן משולשים. לארבעון 4 קודקודים, 4 פאות, ו-6 מקצועות.
אף על פי שלעיתים נתפסת התיבה כגוף הפשוט ביותר, תואר זה שייך דווקא לארבעון. הוא מכיל את מספר הקדקודים המזערי הדרוש כדי להיות גוף תלת־ממדי ולא מישורי, שכן דרך כל שלוש נקודות עובר מישור.
הארבעון הוא 3-סימפלקס, מקרה פרטי של n-סימפלקס (הכללה רב-ממדית של המשולש).
נפח הארבעון נתון על ידי הנוסחה:
כאשר הוא שטח הבסיס ו-h הוא הגובה מהבסיס אל הקודקוד שמעליו.
ארבעון משוכלל[עריכת קוד מקור | עריכה]
ארבעון משוכלל הוא ארבעון שכל פאותיו הן משולשים שווי צלעות.
הארבעון המשוכלל סימטרי במידה רבה ביותר: חבורת הסימטריות שלו פועלת 4-טרנזיטיבית על ארבעת הקודקודים, כלומר, אפשר להעביר, על ידי סיבוב ושיקוף, כל סדרת קודקודים לכל סדרת קודקודים אחרת. חבורת הסימטריות המרחביות של הארבעון המשוכלל איזומורפית לחבורת תמורות . השלד של הארבעון הוא הגרף השלם , וחבורת הסימטריות שלו איזומורפית ל-.
הארבעון המשוכלל הוא אחד מחמשת הגופים האפלטוניים, הידועים גם בשם הפאונים המשוכללים. גוף אפלטוני הוא פאון שכל פאותיו הן אותו מצולע משוכלל (מצולע שווה-צלעות), ובכל אחד מקודקודיו נפגשות פאות באותו מספר.
שטח הפנים A והנפח V של ארבעון משוכלל בעל צלע a הם:
הארבעון המשוכלל הוא דואלי לעצמו. כלומר: אם נסמן בכל אחת מפאותיו של ארבעון את הנקודה האמצעית, ונחבר את כל הנקודות הללו, נקבל ארבעון משוכלל.
מיון הארבעונים על-פי הסימטריות שלהם[עריכת קוד מקור | עריכה]
את הארבעונים אפשר למיין למשפחות, על-פי חבורת הסימטריות שלהם. זהו מיון בעל משמעות בקריסטלוגרפיה, שם ממיינים את הסריגים למחלקות בראבה ולמערכות גבישיות, בין השאר, על-פי חבורת הסימטריות של תא היחידה של הסריג.
הסימטריות של השלד[עריכת קוד מקור | עריכה]
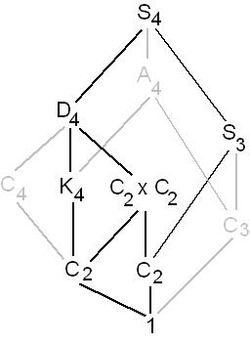

הקודקודים והמקצועות של ארבעון מרכיבים את השלד החד-ממדי שלו, שהוא גרף שממנו אפשר לשחזר את המבנה הגאומטרי, התלת-ממדי. בסימטריות של השלד אפשר לבצע גם פעולות שאינן אפשריות בגוף צפיד, השקולות לשיקוף של המרחב: תמורה של הקודקודים מהווה סימטריה של השלד, אם היא מעתיקה כל מקצוע למקצוע באותו אורך. משום כך יש יותר חבורות סימטריה אפשריות לשלד, על-פי הפירוט הבא.
- חבורת הסימטריות של ארבעון משוכלל היא (אם חבורת הסימטריות מכילה את , שהיא 2-טרנזיטיבית על הקודקודים ולכן טרנזיטיבית בפעולה על המקצועות, הארבעון מוכרח להיות משוכלל).
- חבורת הסימטריות היא החבורה הדיהדרלית אם הארבעון הוא יתדון טטרגונלי, שבו ארבעה מקצועות שווי-אורך ועוד שניים, שאינם נפגשים, שגם שהם שווי-אורך. (הסימטריה הציקלית מסדר 4 מאלצת די שוויונות בין ארכי המקצועות כדי שהחבורה תהיה ).
- חבורת הסימטריות היא החבורה הסימטרית כאשר הארבעון הוא פירמידה ישרה שבסיסה משולש שווה-צלעות. (גם כאן, סימטריה ציקלית מסדר 3 מאלצת את התכונות המקנות גם סימטריית שיקוף ועימה את החבורה ).
- חבורת הסימטריות היא חבורת הארבעה של קליין, , אם הארבעון הוא יתדון רומבי.
- חבורת הסימטריות היא , מסדר 4, וכוללת שני חילופים המחליפים זוגות זרים של קודקודים, אם לארבעון יש ארבעה מקצועות שווי-אורך שאין ביניהם שלושה החולקים קודקוד משותף.
- חבורת הסימטריות היא , ציקלית מסדר 2, עם החלפה של שני זוגות קודקודים, אם לארבעון יש שני זוגות של מקצועות שווי-אורך שאינם נפגשים (והזוג השלישי, שלא כמו ביתדון, בעל אורכים שונים).
- חבורת הסימטריות היא , ציקלית מסדר 2, עם חילוף של זוג קודקודים, אם לארבעון יש שני זוגות של מקצועות שווי-אורך הנפגשים בקודקוד משותף.
- בכל מקרה אחר, חבורת הסימטריות טריוויאלית.
סימטריות הסיבוב המרחביות[עריכת קוד מקור | עריכה]
כל סימטריה של השלד אפשר לממש גם כסימטריה של המרחב כולו, אם מרשים בנוסף לסיבובים, גם לשקף את המרחב. פעולת השיקוף אינה ניתנת למימוש במציאות הפיזיקלית (בשל-כך יודע אדם בין ימינו לשמאלו). ללא שיקופים אפשר לממש רק תמורות זוגיות, ונותרות חמש אפשרויות:
- חבורת סימטריות הסיבוב של ארבעון משוכלל היא, כאמור, .
- חבורת סימטריות הסיבוב של פירמידה ישרה שבסיסה משולש שווה-צלעות היא החבורה הציקלית .
- חבורת סימטריות הסיבוב של יתדון (רומבי או טטרגונלי) היא .
- חבורת סימטריות הסיבוב של ארבעון בעל שני זוגות של מקצועות שווי-אורך שאינם נפגשים (והזוג השלישי, שלא כמו ביתדון, בעל אורכים שונים) היא , ציקלית מסדר 2, עם החלפה של שני זוגות קודקודים.
- בכל מקרה אחר, חבורת הסימטריות טריוויאלית.
קוביית משחק[עריכת קוד מקור | עריכה]

הארבעון משמש כקוביית משחק במשחקי תפקידים בתור ק4. המספרים מופיעים במרכז כל צלע. מאחר שאין לארבעון צד עליון המספר שהתקבל נקבע על פי המספר המופיע במרכז הצלע התחתונה.
ראו גם[עריכת קוד מקור | עריכה]
- מתאן - מולקולה בצורת ארבעון
- ארבעון קטום
- הבעיה השלישית של הילברט
קישורים חיצוניים[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ במילוני האקדמיה ללשון העברית השונים גם: פִּירָמִידָה מְשֻׁלֶּשֶׁת, פִּירָמִידָה מְשֻׁלָּשִׁית, טֶיטְרָאֶדְרוֹן, טֶטְרָאֵדֶר
| חמשת הפאונים האפלטוניים | |||||||||||
| |||||||||||
| מצולעים ופאונים | ||
|---|---|---|
| מושגים | מצולע • פאון • קודקוד • צלע • מקצוע • פאה • זווית חיצונית • אלכסון | |
| מצולעים | ||
| לפי מספר צלעות | משולש • מרובע • מחומש • משושה • משובע • מתומן | |
| משולשים | משולש ישר-זווית • משולש שווה-שוקיים • משולש שווה-צלעות | |
| מרובעים | מקבילית • טרפז • טרפז שווה-שוקיים • מרובע ציקלי • דלתון • דלתון ריצוף • מעוין • מלבן • ריבוע | |
| כוכבים | פנטגרם • מגן דוד • אניאגרם | |
| תכונות | מצולע משוכלל • מצולע שווה-צלעות • מצולע קמור • כוכב | |
| פאונים | ||
| פאונים משוכללים | ארבעון • קובייה • תמניון • תריסרון • עשרימון | |
| פאונים ארכימדיים | ארבעון קטום • קובוקטהדרון • קובייה קטומה • תמניון קטום • רומביקובוקטהדרון • קובוקטהדרון קטום • קובייה מסותתת • איקוסידודקהדרון • דודקהדרון קטום • איקוסהדרון קטום • רומביקוסידודקהדרון • איקוסידודקהדרון קטום • דודקהדרון מסותת | |
| פאונים אחרים | פירמידה • מנסרה • אנטי-מנסרה • מקבילון • מעוינון • תיבה • איקוסיטטרהדרון | |
| תכונות | פאון משוכלל • פאון משוכלל למחצה • פאון ארכימדי | |
| הכללות | ||
| הכללות | סימפלקס • היפרקובייה • טסרקט | |















