שיטת ניוטון-רפסון
שיטת ניוטון-רפסון (או כלל ניוטון) היא אלגוריתם יעיל באנליזה נומרית, למציאת שורשים של פונקציה ממשית כלשהי, דהיינו נקודות בהן הפונקציה מתאפסת. השיטה פותחה באופן בלתי תלוי בידי אייזק ניוטון וג'וזף רפסון.
תיאור[עריכת קוד מקור | עריכה]
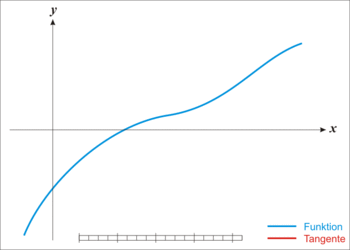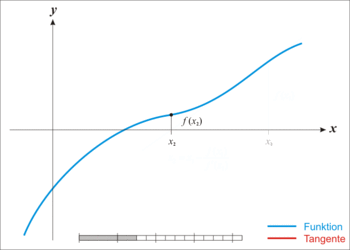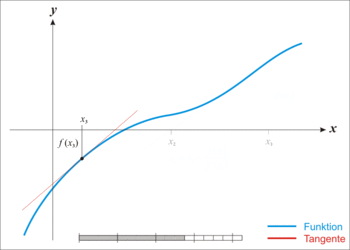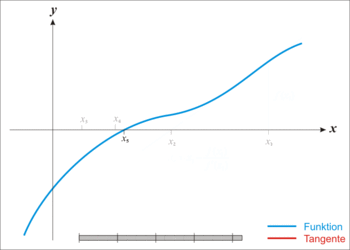
השיטה מבוססת על הרעיון הבא: בהינתן פונקציה שאת השורש שלה אנחנו מחפשים, ואנו מגבילים את עצמנו לתחום בו יש לפונקציה רק שורש אחד, אם נבחר נקודה קרובה לשורש, השורש של המשיק לפונקציה באותה נקודה יהיה קרוב יותר לשורש שאנו מחפשים. בכל איטרציה של הלולאה, יתקבל קירוב טוב יותר ויותר.
סדר הפעולות בשיטת ניוטון רפסון הוא:
- בחירת נקודה קרובה לשורש המבוקש.
- חישוב שיפוע המשיק לפונקציה בנקודה זו; זוהי הנגזרת של הפונקציה באותה נקודה.
- חישוב משוואת המשיק באמצעות גאומטריה אנליטית.
- מציאת שורש המשיק, כלומר הנקודה בה המשיק חותך את ציר ה-x.
אם בחירת הנקודה ההתחלתית הייתה טובה, הנקודה החדשה שהתקבלה קרובה יותר ממנה לשורש, ויש לחזור על התהליך עם הנקודה החדשה כנקודת ההתחלה. אם לא, הנקודה המתקבלת תחרוג מהתחום הנידון. תחת תנאים מסוימים ניתן להבטיח שהשיטה תעבוד היטב, גם עבור נקודות התחלתיות רחוקות מאוד מהשורש.
ניסוח מתמטי[עריכת קוד מקור | עריכה]

בערך זה |

תהי פונקציה גזירה בקטע . נתחיל את האיטרציה מהנקודה . שיפוע המשיק לפונקציה בנקודה זו הוא .
אם כך, אנחנו מחפשים את משוואת הישר שעובר דרך הנקודה ושיפועו . זהו למעשה הקירוב הליניארי לפונקציה בנקודה . על פי הגאומטריה האנליטית נקבל שמשוואה זו היא . מאחר שאנו מחפשים את החיתוך של ישר זה עם ציר , נציב ונקבל, לאחר העברת אגפים:
נסתכל כעת בסדרה המוגדרת רקורסיבית על ידי
דוגמאות[עריכת קוד מקור | עריכה]
נראה כיצד ניתן להשתמש בשיטה זו כדי לחשב בקלות שורשים. נניח כי אנו רוצים לחשב את עבור כלשהו. מספר זה הוא השורש החיובי של הפונקציה . נגזור ונקבל . בתור אבר ראשון באיטרציה נבחר את עצמו (ניתן להוכיח כי בבחירה זו מובטח שהשיטה תיתן את הפתרון). כלומר, נביט בסדרה המוגדרת כך:
בעזרת משוואה זו, ניתן לחשב תוך לכל היותר 10 איטרציות ערך מדויק עד 10 ספרות אחרי הנקודה של כל מספר עד 1,000. במספר איטרציות גדול יותר, השיטה עובדת עבור כל מספר ממשי חיובי.
נדגים עבור :
בתוך ארבע איטרציות הושג דיוק של 10 ספרות אחרי הנקודה. לפעמים נוח יותר להוציא גורם משותף של חצי, ולהתייחס לחישוב כאל ממוצע בין שני ערכים, דבר שגם מסביר אינטואיטיבית את החישוב.
דוגמה נוספת, מעט יותר מסובכת: :
הנגזרת היא: .
נסמן:
ושוב, לאחר ארבע איטרציות בלבד הושג דיוק של 10 ספרות אחרי הנקודה.
התכנסות[עריכת קוד מקור | עריכה]
עבור פונקציות מסוימות, ניתן להוכיח ששיטת ניוטון-רפסון תתכנס לפתרון המבוקש, בהתחשב בנגזרת הראשונה והשנייה:
תהא גזירה פעמיים ברציפות בקטע , יש לה שורש יחיד בקטע זה - , ונניח שהנגזרת והנגזרת השנייה אינן משנות סימן בקטע. אם כל הערכים הם חיוביים, או ששניים מהם שליליים והשלישי חיובי, אז האיטרציה מתכנסת לפתרון.
במקרים אלו ניתן גם לתחום את גודל השגיאה, על ידי אי השוויון כאשר .
הוכחה[עריכת קוד מקור | עריכה]
ההוכחה מתבססת על שימוש בטור טיילור מסדר שני. נראה אותה עבור המקרה הראשון - עבור שאר המקרים הרעיון זהה.
חלק א: הוכחת התכנסות[עריכת קוד מקור | עריכה]
תהי הסדרה המתקבלת מאיטרצית ניוטון. נניח כי . כעת נפתח את טור טיילור של סביב , עם טעות מסדר שני:
כעת נשתמש בהגדרת הסדרה ונקבל:
נעביר אגפים:
כעת נזכור כי על פי הנתון ולכן הביטוי באגף ימין חיובי. מכאן כי גם הביטוי באגף שמאל חייב להיות חיובי. על פי הנתון, ולכן בהכרח מתקיים:
כלומר
הראינו שהסדרה חסומה מלרע על ידי . כעת נראה שזו סדרה יורדת: על פי הנוסחה ידוע כי . הנגזרת חיובית, כלומר הפונקציה עולה בקטע, ומאחר ש- הרי ש- ולכן ומכאן שמתקיים . הראינו שהסדרה יורדת.
משפט בסיסי באנליזה קובע כי סדרה יורדת וחסומה מלרע מתכנסת לגבול. אם כן, נסמן . אז מתקיים: ולכן ונקבל מיידית . מכיוון ש- הוא השורש היחיד בקטע, . הראינו שהסדרה מתכנסת אל השורש המבוקש.
חלק ב': הוכחת הערכת השגיאה[עריכת קוד מקור | עריכה]
נפתח הפעם את טור טיילור של סביב הנקודה :
כעת, לפי משפט הערך הממוצע של לגראנז' קיימת המקיימת:
וקיבלנו:
. כעת נציב את :
.
ובכך הושלמה ההוכחה.
הכללות[עריכת קוד מקור | עריכה]
לפונקציות מרוכבות[עריכת קוד מקור | עריכה]
בשנת 1879 פרסם המתמטיקאי ארתור קיילי לראשונה הכללה של השיטה לפונקציות מרוכבות.

כאשר עוסקים בפונקציות מורכבות, ניתן ליישם ישירות את שיטת ניוטון כדי למצוא את האפסים שלהן[1]. לכל אפס יש נקודת משיכה במישור המרוכב, קבוצת כל ערכי ההתחלה שגורמים לשיטה להתכנס לאפס המסוים הזה. ניתן למפות קבוצות כאלה כמו בתמונה המוצגת. עבור פונקציות מורכבות רבות, גבולות אגני המשיכה הם פרקטלים.
במקרים מסוימים ישנם אזורים במישור המורכב שאינם נמצאים באף אחד מאגני המשיכה הללו, כלומר האיטרציות אינן מתכנסות. לדוגמה[2], אם משתמשים בתנאי התחלתי אמיתי כדי לחפש שורש של , כל האיטרציות הבאות יהיו מספרים ממשיים ולכן האיטרציות לא יכולות להתכנס לאף אחד מהשורשים, מכיוון ששני השורשים אינם אמיתיים. במקרה זה כמעט כל התנאים ההתחלתיים האמיתיים מובילים להתנהגות כאוטית, בעוד שמצבים ראשוניים מסוימים חוזרים עד אינסוף או למחזורים חוזרים בכל אורך סופי.
המתמטיקאי קורט מקמלן הראה כי לכל אלגוריתם איטרטיבי אפשרי טהור הדומה לשיטת ניוטון, האלגוריתם יתפצל בחלק מהאזורים הפתוחים של המישור המורכב כשהוא מיושם על פולינום כלשהו בדרגה 4 ומעלה. עם זאת, מקמולן נתן אלגוריתם מתכנס בדרך כלל לפולינומים בדרגה 3.[3]
לממדים גבוהים[עריכת קוד מקור | עריכה]
ניתן להכליל את שיטת ניוטון-רפסון גם לשדות וקטורים על ידי החלפת השימוש בנגזרת לשימוש ביעקוביאן:
בהינתן פונקציה וקטורית נרצה למצוא וקטור כך ש-. כלומר, לפתור מערכת של m משוואות (לא בהכרח ליניאריות) ב-k נעלמים.
אם k=m, נוכל לעשות זאת באמצעות כלל הנסיגה,
אם m>k, מטריצת היעקוביאן בהכרח איננה הפיכה ולכן אין לה מטריצה הופכית. במקרה זה נחליף את המטריצה ההופכית בנוסחה לעיל במטריצה:
לאופטימיזציה[עריכת קוד מקור | עריכה]
במקרים רבים, אופטימיזציה מצריכה מציאת נגזרת של פונקציה והשוואתה לאפס. דרך אחת לבצע זאת היא על ידי שיטת ניוטון-רפסון לנגזרת. במילים אחרות, תחת קיומה של נגזרת שנייה ל- ותנאים טכניים נוספים, הסדרה שמוגדרת על ידי כלל הנסיגה
קיימת הרחבה גם של שיטה זו לממדים גבוהים יותר.
השוואה לשיטות אחרות[עריכת קוד מקור | עריכה]
יתרונה הגדול של שיטת ניוטון-רפסון הוא סדר ההתכנסות הריבועי. חסרונותיה העיקריים:
- השיטה לא תמיד מתכנסת.
- לא תמיד ניתן לחשב את הנגזרת ולעיתים החישוב מסורבל.
כדי להתגבר על החסרון הראשון, משתמשים לעיתים בשיטה אחרת, המבטיחה התכנסות (למשל שיטת החצייה), כדי להגיע לסביבת השורש, ושם מפעילים את שיטת ניוטון-רפסון. אם לא ניתן לחשב את הנגזרת, או שחישוב הנגזרת גוזל משאבי חישוב, משתמשים בשיטת המיתר, שסדר ההתכנסות שלה הוא קרוב לזה של שיטת ניוטון-רפסון.
כדי להתגבר על החסרון השני משתמשים בשיטות קווזי-ניוטוניות כדוגמת שיטת ברוידן אשר דורשות חישוב יחיד של הנגזרת (או היעקוביאן) ולאחר מכן שיערוך של היעקוביאן בנקודה הבאה ע"פ הנקודה הנוכחית. שיטות מסוג זה נמצאות בשימוש רחב באלגוריתמי אופטימזציה ממוחשבים.
אם השורש הוא בעל ריבוי גדול מ-1, השיטה תתכנס, אך קצב ההתכנסות לא יהיה ריבועי, אלא ליניארי (סדר ההתכנסות הוא 1). אם השורש הוא מסדר השיטה האיטרטיבית המוגדרת על ידי תתכנס, וקצב ההתכנסות יהיה ריבועי.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- שיטת ניוטון-רפסון, באתר MathWorld (באנגלית)
 שיטת ניוטון רפסון במחשבון, סרטון באתר יוטיוב
שיטת ניוטון רפסון במחשבון, סרטון באתר יוטיוב
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ Peter Henrici, Applied and Computational Complex Analysis, 1974
- ^ Gilbert Strang, A Chaotic Search for i, The College Mathematics Journal 22, 1991-01-01, עמ' 3–12 doi: 10.1080/07468342.1991.11973353
- ^ Curt McMullen, Families of Rational Maps and Iterative Root-Finding Algorithms, Annals of Mathematics 125, 1987, עמ' 467–493 doi: 10.2307/1971408

![{\displaystyle f:[a,b]\rightarrow \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc0d2d0b70573525d149ab82948308455d1853d0)
![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)












































































